详解快速傅里叶变换(FFT)（快速傅里叶变换物理意义）

 

道生一，一生二，二生三，三生万物 ——《道德经》FFT是加快DFT的一种算法，本质仍为求各频率成分前的系数通过迭代的方式，FFT将乘法运算复杂度从 O(n2)O(n^2)降到 O(nlog2⁡n)O(n\log_2n)。

。关于傅里叶变换详细推导，可参考：Hsuty：傅里叶级数(Fourier series)与傅里叶变换(Fourier transform)126 赞同 · 15 评论文章

有趣小故事：Cooley(库利) 和 Tukey(图基) 合作的FFT名篇：An algorithm for the machine calculation of complex Fourier series

是站在 I. J. Good肩上的 (Good 采用的是素因子分解法 the prime factor algorithm (PFA)来加快计算)但是，这篇论文第一次投出去惨遭拒稿这篇论文非常短，只有4页半A4纸，两篇参考文献，其论文中的推导方式非常难懂。

论文出来后，很多人都搞不明白其算法的真正原理，直到Tom Stockham和Charlie Rader 画了一个蝶形图，终于参破玄机目前(2022年2月)，此论文已被引用17000多次

1 离散傅里叶变换(DFT)定义在复数域内，DFT定义如下：Xk=∑n=0N−1xne−i2πnNkX_k=\sum_{n=0}^{N-1}{x_ne^{-i\frac{2\pi n}{N}k}} ,

k=0,1,...,N−1k=0,1,...,N-1 .展开各项：X0=x0e−i2π0N0+x1e−i2π1N0+...+xN−1e−i2π(N−1)N0X_0=x_0e^{-i\frac{2\pi 0}{N}0}+x_1e^{-i\frac{2\pi 1}{N}0}+...+x_{N-1}e^{-i\frac{2\pi (N-1)}{N}0}

X1=x0e−i2π0N1+x1e−i2π1N1+...+xN−1e−i2π(N−1)N1X_1=x_0e^{-i\frac{2\pi 0}{N}1}+x_1e^{-i\frac{2\pi 1}{N}1}+...+x_{N-1}e^{-i\frac{2\pi (N-1)}{N}1}

...XN−1=x0e−i2π0N(N−1)+x1e−i2π1N(N−1)+...+xN−1e−i2π(N−1)N(N−1)X_{N-1}=x_0e^{-i\frac{2\pi 0}{N}(N-1)}+x_1e^{-i\frac{2\pi 1}{N}(N-1)}+...+x_{N-1}e^{-i\frac{2\pi (N-1)}{N}(N-1)}

令 e−i2πN=w=WNe^{-i\frac{2\pi }N}=w=W_N将上式用矩阵表示为：[X0X1X2⋮XN−1]=[11⋯11w⋯wN−11w2⋯w2(N−1)⋮⋮⋮⋮1wN−1⋯w(N−1)

2][x0x1x2⋮xN−1]\begin{bmatrix} X_0\\ X_1\\ X_2\\ \vdots\\ X_{N-1} \end{bmatrix}= \begin{bmatrix} 1&1&\cdots &1\\ 1&w&\cdots&w^{N-1}\\ 1&w^2&\cdots&w^{2(N-1)}\\ \vdots&\vdots& \vdots&\vdots\\ 1&w^{N-1}&\cdots&w^{(N-1)^2} \end{bmatrix} \begin{bmatrix} x_0\\ x_1\\ x_2\\ \vdots\\ x_{N-1} \end{bmatrix}

因此，DFT可简写为： X=FxX=Fx ,注意观察：FF 中各列是彼此正交的注意： e−i2πN=w=WNe^{-i\frac{2\pi }N}=w=W_N 为复数域上，1的N次方的第二个根， WN0

=1W_N^0=1 .此时，完成N个点DFT，需计算 N2N^2 次乘法，即矩阵F中每个元素都会参与一次乘法，共 N2N^2 个元素；N(N-1)次加法，即每完成一个点需要N-1次加法，共N个点2 快速傅里叶变换(FFT)出场。

1965年, Cooley(库利) 和 Tukey(图基) 发表An algorithm for the machine calculation of complex Fourier series 大大加快了DFT计算。

实际上，这两位作者只是重新发明了高斯在1805年就已经提出的算法（此算法在历史上数次以各种形式被再次提出）

历史上，提出过类似FFT算法的人物：

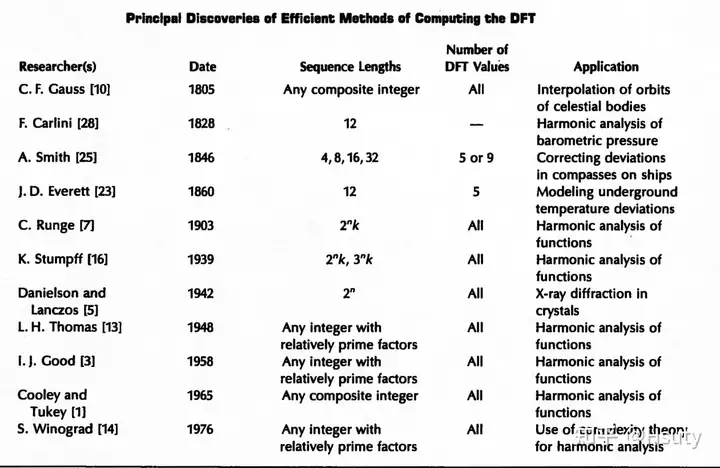
Source: Gauss and the History of the Fast Fourier Transform目前(2022年2月)，库利和图基的论文已被引用17000多次。

FFT能够实现的根本原因是：复数域内，1的N次方根的周期性与对称性，如下图所示

Source: https://ccrma.stanford.edu/~jos/st/Nth_Roots_Unity.html利用周期性与对称性，怎么加快 X=FxX=Fx 的运算呢？从上图可知，W89

=W81{W}^{9}_8={W}^{1}_8WNk+N=WNk{W}^{k+N}_N={W}^{k}_N这是周期性；W80=−W84{W}^{0}_8=-{W}^{4}_8WNk+N2=−WNk{W}^{k+\frac{N}{2}}_N=-{W}^{k}_N

这是对称性此外，还利用一个很重要的性质，W82=W41{W}^{2}_8={W}^{1}_4WNmkn=WNmkn{W}^{mkn}_N={W}^{kn}_\frac{N}{m}此时，N/m为正整数这可以理解为某种降维，将非常高的次幂降到最基本的N个根上。

2.1 代数运算角度理解Xk=∑n=0N−1xne−i2πnNkX_k=\sum_{n=0}^{N-1}{x_ne^{-i\frac{2\pi n}{N}k}}=∑n=0N−1x2ne−i2π(2n)N

k+∑n=0N−1x2n+1e−i2π(2n+1)Nk=\sum_{n=0}^{N-1}{x_{2n}e^{-i\frac{2\pi (2n)}{N}k}} +\sum_{n=0}^{N-1}{x_{2n+1}e^{-i\frac{2\pi (2n+1)}{N}k}}

=∑n=0N−1x2nWN2nk+∑n=0N−1x2n+1WN(2n+1)k=\sum_{n=0}^{N-1}{x_{2n}} W_N^{2nk}+\sum_{n=0}^{N-1}{x_{2n+1}} W_N^{(2n+1)k}

=∑n=0N−1x2nWN2nk+WNk∑n=0N−1x2n+1WN2nk=\sum_{n=0}^{N-1}{x_{2n}} W_N^{2nk}+W_N^k \sum_{n=0}^{N-1}{x_{2n+1}} W_N^{2nk}

=even+WNnodd=even+W_N^n odd在这个计算过程中，我们只需计算前一半的N/2个点，对于后一半的点，利用对称性：WNk+N2=−WNk{W}^{k+\frac{N}{2}}_N=-{W}^{k}_N

易得：Xk+N2=∑n=0N−1x2nWN2n(k+N2)−WNk∑n=0N−1x2n+1WN2n(k+N2)X_{k+\frac{N}{2}}=\sum_{n=0}^{N-1}{x_{2n}} W_N^{2n(k+\frac{N}{2})}-W_N^k \sum_{n=0}^{N-1}{x_{2n+1}} W_N^{2n(k+\frac{N}{2})}

注意： WNnN=e−i2πNNn=1W_N^{nN}=e^{-i\frac{2\pi }NNn}=1因此，上式化简为：Xk+N2=∑n=0N−1x2nWN2nk−WNk∑n=0N−1x2n+1WN2n

kX_{k+\frac{N}{2}}=\sum_{n=0}^{N-1}{x_{2n}} W_N^{2nk}-W_N^k \sum_{n=0}^{N-1}{x_{2n+1}} W_N^{2nk}=even

−WNnodd=even-W_N^n odd因此，后一半数只需把加号变减号，乘法计算量减半，即 O(n2)→O(n2)2O(n^2)\rightarrow O(\frac{n}{2})^2 ,如此循环下去，可大大加快计算，这就是FFT。

最终乘法计算量为： N2log2⁡N\frac{N}{2}\log_2 N 计算流程用蝶形图表示一目了然：注意：顺序(0,1,2,...)输入，输出是二进制位反转的(倒置)，即：0, 000 --> 000, 0;。

1, 001 --> 100, 4;2, 010 --> 010, 2;3, 011 --> 110, 6;4, 100 --> 001, 1;5, 101 --> 101, 5;6, 110 -- > 011, 3;

7, 111 --> 111, 7.

2.2 矩阵分解角度理解用矩阵观点看，FFT采样了如下形式的矩阵分解，将稠密矩阵 FF 变成了3个特殊的稀疏矩阵相乘的形式若 N=1024N=1024 ，F1024=[I512D512I512−D512。

][F512F512][even−oddpermutation]F_{1024}= \begin{bmatrix} I_{512}&D_{512}\\ I_{512}&-D_{512} \end{bmatrix} \begin{bmatrix} F_{512}& \\ &F_{512} \end{bmatrix} \begin{bmatrix} even-odd\\ permutation \end{bmatrix}

,其中， II 是单位阵， DD 是对角阵，even-odd permutation是奇偶项交换阵 PP 利用迭代方法，可继续分解下去（迭代编程易实现）F512→F256→F128→F64→F32→F

16→F8→F4→F2F_{512}\rightarrow F_{256}\rightarrow F_{128}\rightarrow F_{64}\rightarrow F_{32} \rightarrow F_{16} \rightarrow F_{8} \rightarrow F_{4} \rightarrow F_{2}

当N=4时，F4=[11111ii2i31i2i4i61i3i6i9]F_4=\begin{bmatrix} 1&1&1&1\\ 1&i&i^2&i^3\\ 1&i^2&i^4&i^6\\ 1&i^3&i^6&i^9\\ \end{bmatrix}

,FFT分解为：F4=[111i1−11−i][111i2111i2][1111]F_4= \begin{bmatrix} 1& &1&\\ &1&&i\\ 1&&-1&\\ &1&&-i \end{bmatrix} \begin{bmatrix} 1&1&&\\ 1&i^2&&\\ &&1&1\\ &&1&i^2\\ \end{bmatrix} \begin{bmatrix} 1&&&\\ &&1&\\ &1&&\\ &&&1\\ \end{bmatrix}

,观察even-odd permutation矩阵：其作用是将偶数项提前，奇数项置后，如：[1111][x0x1x2x3]=[x0x2x1x3]\begin{bmatrix} 1&&&\\ &&1&\\ &1&&\\ &&&1\\ \end{bmatrix} \begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3\\ \end{bmatrix} = \begin{bmatrix} x_0\\ x_2\\ x_1\\ x_3\\ \end{bmatrix}

,分析FFT计算过程,计算 [I512D512I512−D512][F512F512]\begin{bmatrix} I_{512}&D_{512}\\ I_{512}&-D_{512} \end{bmatrix} \begin{bmatrix} F_{512}& \\ &F_{512} \end{bmatrix}

，由于单位阵乘上任何矩阵都等于其本身，因此只有对角阵参与乘法运算每一层有 N2\frac{N}{2} 次乘法(还有 N2\frac{N}{2} 次直接在前 N2\frac{N}{2} 结果上填一个负号就行)，后面的交换矩阵不涉及乘法运算。

因此，FFT所需乘法次数为： N2log2⁡N\frac{N}{2}\log_2 N .推荐阅读1 关于FFT，通信大佬 Alan V. Oppenheim(奥本海姆)讲解数字信号处理-奥本海姆(Discrete-Time Signal Processing-by Alan V. Oppenheim-2015年edx公开课 )_哔哩哔哩_bilibili

​www.bilibili.com/video/BV1Fg41157we?p=58

2 关于FFT历史：Heideman, M. T., Johnson, D. H., & Burrus, C. S. (1985). Gauss and the history of the fast Fourier transform.

Archive for history of exact sciences, 265-277.