当你在游戏里计算角色技能冷却的衰减速率,或是刷短视频时观察点赞量随时间的变化曲线,其实都在不经意间触碰了微积分的核心 —— 极限。这个听起来自带 “高冷学霸” 标签的数学概念,并非只存在于教科书的公式里,它更像是隐藏在生活各个角落的算法密码,而其中最关键的两把钥匙,就是被称为 “微积分守门人” 的两个重要极限。今天我们就用潮流视角拆解这两个数学 “顶流”,看看它们如何在数据时代玩转无限与有限的终极博弈。
很多人第一次见到极限符号时,都会被那只 “趴着的 s”(∫)和趋近符号(→)搞得晕头转向,仿佛在看一门外星语言。但其实极限的本质特别接地气:就像你排队买网红奶茶,前面的人越来越少,你与柜台的距离不断趋近于零,却永远不会真正 “穿越” 到柜台后面 —— 这种 “无限接近却不重合” 的状态,就是极限最直观的写照。而两个重要极限,就是将这种 “无限游戏” 转化为精确计算的终极法则,它们一个掌控着三角函数与多项式的 “跨界对话”,一个解锁了指数增长的 “终极形态”,堪称微积分世界里的 “流量担当”。
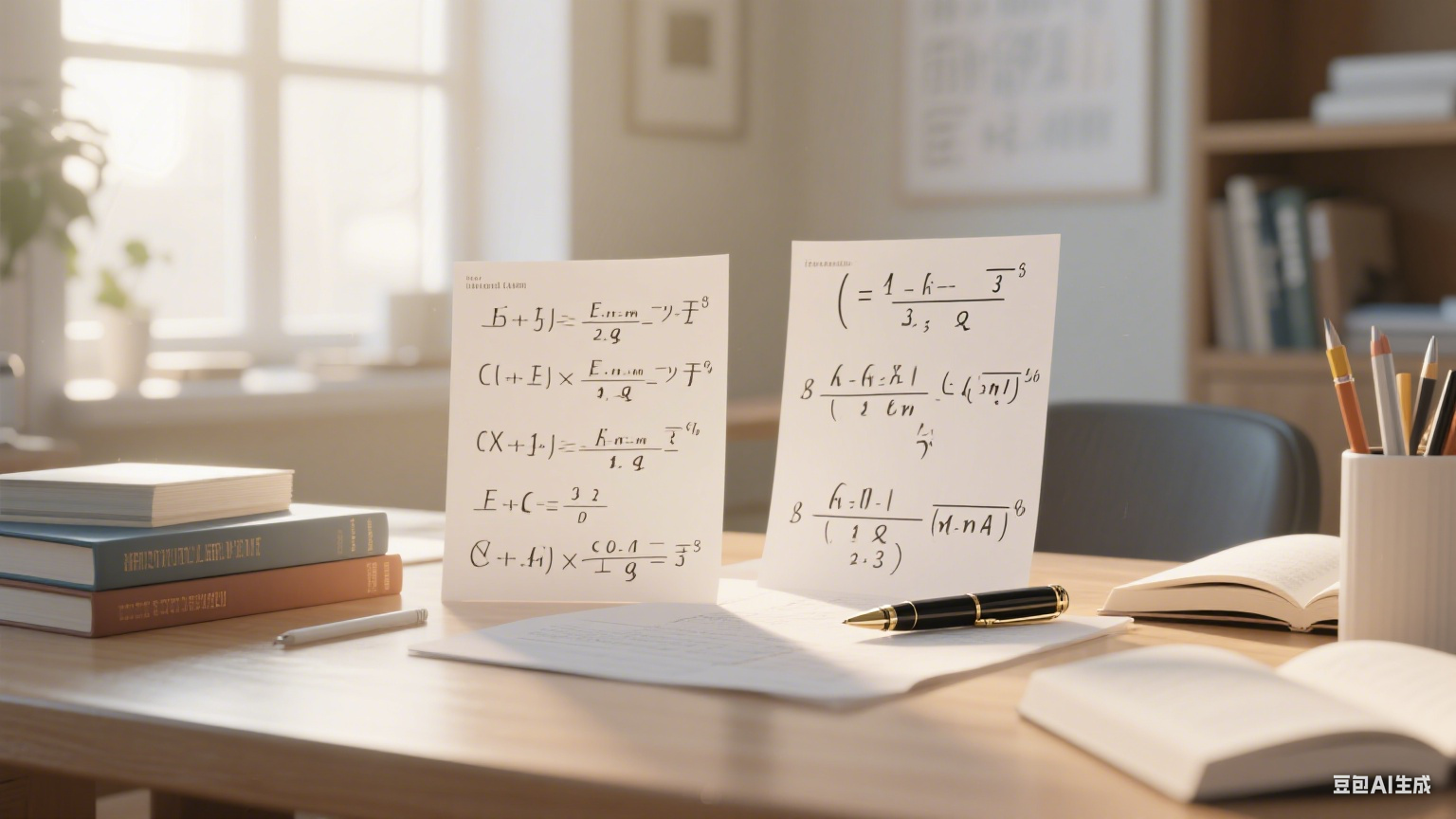
(注:此处为示例图片链接,实际使用时可替换为包含 sinx/x 在 x 趋近于 0 时的趋近曲线、(1+1/x)^x 在 x 趋近于无穷时的渐进线,以及几何辅助图形的高清示意图,建议采用赛博朋克风格配色,突出数学与潮流的碰撞感)
先来看第一个重要极限:\(\lim_{x \to 0} \frac{\sin x}{x} = 1\)。这个看似简单的分式,藏着三角函数与线性函数的 “破冰密码”。我们可以用一个潮流场景理解它:假设你在玩一款 3D 建模游戏,需要绘制一个扇形图案,当扇形的圆心角 x(单位:弧度)越来越小时,扇形的弧长\(\sin x\)和对应的弦长 x 会越来越接近,就像两件不同风格的潮牌单品,在尺寸不断缩小的过程中,逐渐变得 “百搭”。从数学本质来说,这个极限解决了三角函数在原点处的 “可导性” 问题 —— 就像给原本不兼容的设备装了适配器,让微积分能够顺利处理三角函数的导数运算。
在实际应用中,这个极限堪称 “精度救星”。比如在设计 VR 眼镜的视野角度时,当视角偏差 x 很小时,\(\sin x\)可以近似为 x,误差率几乎可以忽略不计,这让工程师在计算光学参数时省去大量复杂运算;再比如在短视频平台的滤镜算法中,当处理微小角度的图像旋转时,利用这个极限可以快速实现像素点的坐标转换,既保证了画面流畅度,又不会出现明显的失真。更有意思的是,这个极限还藏在潮牌设计的细节里 —— 某些品牌的 logo 采用了圆弧与直线的过渡设计,当圆弧半径趋近于零时,圆弧与直线的衔接处就会呈现出\(\frac{\sin x}{x}\)趋近于 1 的平滑效果,让视觉感受更舒适。
接下来登场的第二个重要极限,堪称 “指数增长的终极形态”:\(\lim_{x \to \infty} (1 + \frac{1}{x})^x = e\)(其中 e 是自然常数,约等于 2.71828)。这个极限的神奇之处在于,它将 “有限次迭代” 与 “无限增长” 完美结合,就像你在社交平台上运营账号,每次发布内容的曝光量增长 1/x,当发布次数 x 不断增加时,账号的总影响力会逐渐趋近于 e 倍的初始值 —— 这就是复利效应在数学世界的 “终极表达”。如果你觉得这个比喻不够直观,不妨想想奶茶店的 “第二杯半价” 活动:假设每杯奶茶原价 1 元,每次购买都能享受 “加 1 元多 1 杯” 的折扣(相当于每次增长 1/x,x 为购买次数),当你无限次购买时,平均每杯奶茶的成本就会趋近于 1/e 元,这就是这个极限在消费场景中的趣味映射。
从数学史上看,这个极限的发现堪称 “微积分的高光时刻”。它不仅定义了自然常数 e,还为指数函数和对数函数的导数计算提供了 “金钥匙”。在当下的大数据时代,这个极限更是成为了算法设计的 “核心引擎”:比如在推荐系统中,用户的兴趣权重会随着浏览次数的增加呈现\((1 + \frac{1}{x})^x\)的增长趋势,当 x 足够大时,权重会稳定在 e 倍左右,这让推荐算法既能保持个性化,又不会出现 “信息茧房” 过载;在加密货币的挖矿机制中,算力的增长模型也与这个极限密切相关,矿工的收益会随着算力投入的增加逐渐趋近于 e 倍的基准值,这也是为什么加密货币市场会呈现出 “初期爆发式增长,后期逐渐平稳” 的趋势。
更值得一提的是,这两个重要极限并非孤立存在,它们在微积分的 “宇宙” 中有着千丝万缕的联系。比如对第一个极限两边取自然对数,再经过求导运算,就能推导出第二个极限的表达式;而将第二个极限中的 x 替换为\(\frac{1}{t}\),又能与第一个极限形成巧妙的呼应。这种 “你中有我,我中有你” 的关系,像极了潮流圈的 “联名合作”—— 两个看似独立的品牌,通过跨界联动创造出 1+1>2 的效果,而两个重要极限的协同作用,也让微积分能够轻松应对从几何计算到物理建模的各种复杂问题。
在潮流文化中,“解构” 与 “重组” 是永恒的主题,而两个重要极限恰恰是数学世界里的 “解构大师”。它们将复杂的函数关系拆解为简单的极限形式,再通过重组构建出更强大的运算体系,这种思维方式与潮牌设计师将传统元素拆解重构、打造新风格的理念不谋而合。比如某些设计师将经典的格纹图案拆解为无数个微小的三角形,再通过\(\lim_{x \to 0} \frac{\sin x}{x} = 1\)的原理重新排列,创造出极具未来感的新图案;而在音乐制作中,制作人会将声音波形拆解为无数个正弦函数,再利用第二个重要极限的原理调整声波的频率,让音乐呈现出更丰富的层次感。
随着元宇宙、人工智能等新兴领域的快速发展,两个重要极限的应用场景也在不断拓展。在元宇宙的虚拟建筑设计中,工程师需要利用第一个重要极限计算曲面与平面的衔接精度,让虚拟空间的视觉效果更接近现实;在 AI 绘画的算法中,第二个重要极限被用来优化图像生成的迭代速度,让 AI 能够在更短时间内生成高质量的作品。可以说,这两个看似古老的数学概念,正在以全新的姿态赋能潮流科技,成为连接数学理论与现实应用的 “桥梁”。
或许有人会问,在这个 AI 能自动计算极限的时代,我们还需要理解这些数学原理吗?答案是肯定的。就像潮牌爱好者不仅要知道衣服的款式,还要了解背后的设计理念一样,理解两个重要极限的本质,能让我们更清晰地看清数据背后的逻辑,在面对复杂问题时拥有更深刻的洞察力。当你下次在游戏里调整角色的参数、在社交平台上分析数据趋势,或是在奶茶店计算优惠活动时,不妨试着用这两个重要极限的思维方式去思考,或许会发现一个全新的数学潮流世界。那么,你准备好拿起这两把 “微积分钥匙”,解锁更多生活中的数学奥秘了吗?
免责声明:文章内容来自互联网,本站仅提供信息存储空间服务,真实性请自行鉴别,本站不承担任何责任,如有侵权等情况,请与本站联系删除。
