最全的功率计算公式（功率计算的基本公式）

 

概述

功率包括电功率、机械功率。电功率又包括直流电功率、交流电功率和射频功率；交流功率又包括正弦电路功率和非正弦电路功率；机械功率又包括线位移功率和角位移功率，角位移功率常见于电机输出功率；电功率还可分为瞬时功率、平均功率（有功功率）、无功功率、视在功率。在电学中，不加特殊声明时，功率均指有功功率。在非正弦电路中，无功功率又可分为位移无功功率，畸变无功功率，两者的方和根称为广义无功功率。

本文列出了上述所有功率计算公式，文中p(t)指瞬时功率。u(t)、i(t)指瞬时电压和瞬时电流。U、I指电压、电流有效值，P指平均功率。

1普遍适用的功率计算公式

　　在电学中，下述瞬时功率计算公式普遍适用

　　注：有关电学瞬时功率计算公式的更多信息请阅读：瞬时功率与有功功率计算公式。

在力学中，下述瞬时功率计算公式普遍适用

在电学和力学中，下述平均功率计算公式普遍适用

W为时间T内做的功。

在电学中，上述平均功率P也称有功功率，P=W/T作为有功功率计算公式普遍适用。

在电学中，公式（3）还可用下述积分方式表示

其中，T为周期交流电信号的周期、或直流电的任意一段时间、或非周期交流电的任意一段时间。电学中，公式（3）和（4）的物理意义完全相同。

电学中，对于二端元件或二端电路，下述视在功率计算公式普遍适用：

2直流电功率计算公式

已知电压、电流时采用上述计算公式。

已知电压、电阻时采用上述计算公式。

已知电流、电阻时采用上述计算公式。

　　针对直流电路，下图分别列出了电压、电流、功率、电阻之间相互换算关系。

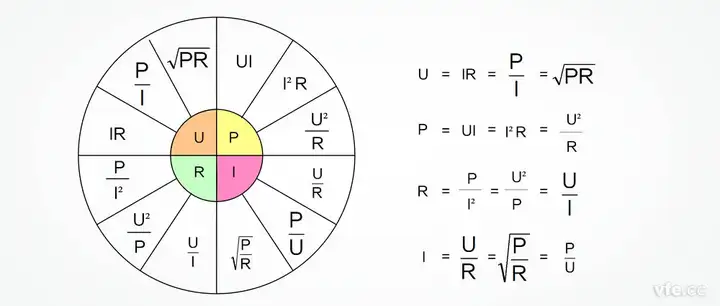
3正弦交流电功率计算公式

正弦交流电无功功率计算公式：

　　正弦交流电有功功率计算公式：

正弦电流电路中的有功功率、无功功率、和视在功率三者之间是一个直角三角形的关系：

当负载为纯电阻时，下式成立：

　　此时，直流电功率计算公式同样适用于正弦交流电路。

4非正弦交流电功率计算公式

非正弦交流电功率计算公式采用普适公式（3）或（4）

对于周期非正弦交流电，将周期交变电压电流进行傅里叶变换，展开为傅里叶级数，有功功率计算公式还可表示为：

　　上式中，当n仅取一个值时，例如：n=1，上式成为基波有功功率计算公式；n=3，上式成为三次谐波有功功率计算公式。

　　在非正弦电路中，有功功率和视在功率的定义不变，然而，此时，电压、电流相位差已经没有明确的物理意义，此时，Q按照下述公式定义：

式中，Un、In为n次谐波的有效值，当n=1时，U1、I1称为基波有效值。

然而，此时，

由于Q与基波及谐波电压、电流的相位角相关，称为位移无功功率。为此，引入畸变无功功率D，畸变无功功率计算公式如下：

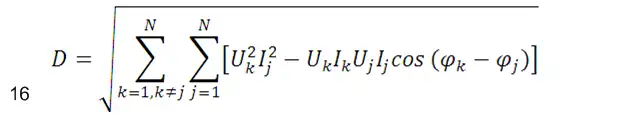
　　畸变无功功率有时也称畸变功率，上式中，N为电压、电流最大谐波次数中的小者。某些文献中也将Q称为无功功率，而将Q和D的方和根称为广义无功功率。

　　对比位移无功功率和畸变无功功率的计算公式，可以发现：Q是相同频率的电压分量与电流分量相位移不同产生的无功；而畸变无功功率则是不同频率电压及电流分量之间产生的无功。这一点很容易理解，前者是因为相同频率分量之间存在相位差。而后者由于频率不同，其相位差始终在变化，当然不会相等，而电压和电流相位不同，就会产生无功。

非正弦电路中，视在功率S、有功功率P、位移无功功率Q、畸变无功功率D满足下述计算公式。

5射频功率计算公式

　　射频功率属于交流电功率，理论上具有与交流电功率相同的计算公式，但是，实际上在超高频和微波频段，有TEM波和非TEM波之分。在TEM波的同轴系统中，电压和电流虽有确切含意，但测量其绝对值很困难。在波导系统中，因为存在不同的电磁模式，电压和电流失去唯一性。在个频段和各传输系统中，功率是单值表征信号强度的重要方法。在射频范围直接测量功率代替了电压和电流的测量。

6三相有功功率计算公式

三相电路中，总有功功率等于各相有功功率的算术和。三相四线制电路中，通常采用三瓦计法分别测量每相的功率，三相有功功率计算公式如下：

　　对于三相三线制电路，也可采用二瓦计法，三相功率计算公式为：

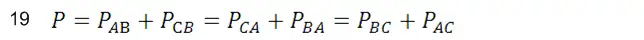
　　注1：二瓦计法适用对称和不对称的三相三线制电路，详细功率计算公式推导请参见：二瓦计与三瓦计法适用场合详解。

　　对于正弦三相对称电路，

　　U、I为线电压、线电流有效值，φ为相电压与相电流的相位差。

或

　　UP、IP为相电压、相电流有效值，φ为相电压与相电流的相位差。

注：采用二瓦计法测量时，每个瓦表的相位差与上述φ有内在联系，但并相同，详细内容请参见：二瓦计法相位与功率因数的关系。

7三相无功功率计算公式

　　在电源和负载都对称的三相三线电路中，可以利用测量有功功率的两表法测出三相无功功率：

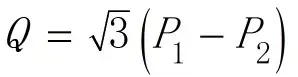
　　P1、P2为两个功率表测量数据

　　三表法适用于电源电压对称、负载对称或不对称的三相三线制和三相四线制电路中：

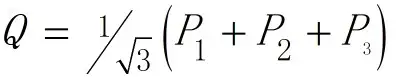
P1、P2、P3分别为三个功率表测量数据

8电动机输出功率计算公式

　　电动机输出功率也称电动机轴功率或机械功率，电动机输出功率计算公式如下：

　　其推导过程如下：

P=FV （a）

F：力，单位为N；V：速度，单位为m/s；P：功率，单位为W

T=FR

F=T/R （b）

T：扭矩，单位为N.m；R：作用半径，单位为m

V=2πRn/60=πR*n/30 （c）

V：线速度，单位为m/s；n：转速，单位为r/min

将（b）、（c）代入（a）

P=πTn/30

若将P的单位变为kW，得到下述电机功率计算公式：

P=πTn/30000=Tn/9549

或

T=9549P/n

注：电机输入功率、输出功率及扭矩的换算公式及详细推导过程请参见：扭矩和功率的计算公式推导及记忆方法。

扭矩和功率的计算公式推导及记忆方法

扭矩和功率及转速的关系式，是电机学中常用的关系式，近期在百度知道上常有看到关于扭矩和功率及转速的相关计算式的问答，一般回答者都是直接给出计算公式，公式中的常数采用近似值，常数往往不容易记住，本文的目的就是帮助大家方便的记住这些公式，并在工程应用中熟练的使用。

1记住扭矩和功率的公式形式

　　扭矩和功率及转速的关系式一般用于描述电机的转轴的做功问题，扭矩越大，轴功率越大；转速越高，轴功率越大，扭矩和转速都是产生轴功率的必要条件，扭矩为零或转速为零，输出轴功率为零。因此，电机空转或堵转就是轴功率等于零的两个特例。

　　功率和扭矩及转速成正比，扭矩和功率的关系式具有如下形式：

　　P=aTN

　　上式中，a为常数，对应的有：

　　T=(1/a)(1/N)P

　　即扭矩和功率成正比，和转速成反比。

记忆方法：

记住扭矩T和功率P成正比，扭矩T和转速N成反比，而系数a不必记忆。

2记住力做功的基本公式

　　提问者通常都知道上述关系式，问题的焦点在于常数a的具体数值。

　　如果不是经常使用该公式，的确很难记住这个常数，本人亦是如此。

　　不过，只要记住扭矩和转速公式的推导方式，可以很快推导出结果，得到系数a的准确值。

　　我们知道力学中力做功的功率计算公式为：

　　P=FV （2）

　　上述公式为力做功的基本公式。然而，基本公式中没有出现扭矩T和转速N。

　　如果我们注意到：扭矩实际上就是力学上的力矩。就很容易联想到扭矩T和力F的关系。

　　由于力矩等于力F和力臂的乘积，而力臂是轴的半径r，因此有：

　　T=Fr或

　　F=T/r（3）

图2 扭矩和力臂的关系

记忆方法：

扭矩的单位是N.m，N是力的单位，m是长度的单位，因此，力等于扭矩除以长度，而长度就是半径r。

3掌握角速度和速度的转换方法

　　第二节告诉我们，扭矩与轴的半径有关，可是，扭矩和功率的关系式（1）中，并无轴半径的参数r，也无力做功基本公式（2）中的速度V。

　　这就引导我们去思考，将速度V变换为转速N后，转速N与扭矩T相乘，应该可以抵消掉轴半径r。实际正是如此：

　　电动机轴面上任意一点的速度与旋转的角速度及轴半径成正比，即：

　　V=ωr（4）

记忆方法：

圆弧的长度等于角度乘以半径，圆周运动的速度等于角速度乘以半径。

4扭矩和功率的基本公式

　　将式（3）和（4）代入式（2），得到：

　　P=Tω（5）

　　式（5）为扭矩和功率的基本公式，这个公式，我们可以按照上述方式推导，不过最好的办法还是直接记住。

记忆方法：

角速度ω和转速N都可以反映转速，采用角速度时，扭矩和功率成正比，扭矩和转速成反比，且正反比的系数均为1，因此，这是扭矩和功率的基本公式。

5单位转换

　　至此，我们还是没有得出扭矩和功率关系式（1）中的常数a。那么，前面的推导，是否过于繁琐呢？

　　当然不是，实际上，式（5）和式（1）具有相同的含义，区别仅仅在于变量的单位。

　　而一个公式中，如果单位不确定，常数是没有意义的。

式（5）中，P、T和ω均采用标准单位，分别为瓦特（W）、牛顿.米（N.m）和弧度/秒（rad/s）。

　　式（1）中，若扭矩和功率的单位不变，转速N采用常用的转/分（r/min）。

　　由于一圈等于2π弧度，1分钟等于60秒，式（5）变换为：

　　P=(2π/60)TN

　　若功率P采用kW为单位，上式变换为：

　　P=(2π/60000)TN

　　60000/2π≈9549代入上式得到：

　　P≈TN/9549

　　T≈9549P/N （6）

　　式（6）就是最常用的扭矩和功率计算公式。

　　若功率较小，单位采用瓦特，式（6）的常数需要除以1000。若转速单位采用转每秒，式（6）的常数需要乘以60。

　　式（6）和式（5）的区别仅仅在于单位的选择，而式（5）才是扭矩和功率的基本公式。

6扭矩和功率及转速关系式记忆方法

扭矩和功率的基本公式为P=Tω，角速度ω可用转速N替代，只要记住使用公式的变量和基本公式中变量的单位转换关系，就可以方便的推导出各种扭矩和功率的计算公式及相关常数的准确数值。