拉普拉斯变换（拉普拉斯变换对应表）

 

1、从傅里叶到拉普拉斯变换

由于一些函数不满足绝对可积的条件，因为求解傅里叶变换就相对困难。为解决这一问题，可以采用一衰减因子 e−σte^{-\sigma t} 乘以信号 f(t)f(t) ，适当的选取 σ\sigma 的值，使得乘积信号 e−σtf(t)e^{-\sigma t}f(t) 当 t→∞t\rightarrow ∞ 时信号的幅度趋近于0，从而使得 e−σtf(t)e^{-\sigma t}f(t) 的傅里叶变换存在。

傅里叶变换表达式：

Fb(σ+jω)=∫−∞+∞f(t)e−σte−jωtdt=∫−∞+∞f(t)e−(σ+jω)tdtF_{b}(\sigma+j\omega)=\int_{-∞}^{+∞}f(t)e^{-\sigma t}e^{-j\omega t}dt=\int_{-∞}^{+∞}f(t)e^{-(\sigma+j\omega) t}dt

相应的傅里叶反变换表达式为：

f(t)e−σt=∫−∞+∞Fb(σ+jω)ejωtdωf(t)e^{-\sigma t}=\int_{-∞}^{+∞}F_{b}(\sigma+j\omega)e^{j\omega t}d\omega

上式两边同时乘以 e−σte^{-\sigma t} 得到：

f(t)=∫−∞+∞Fb(σ+jω)e(jω+σ)tdωf(t)=\int_{-∞}^{+∞}F_{b}(\sigma+j\omega)e^{(j\omega+\sigma) t}d\omega

令 s=σ+jωs=\sigma+j\omega ,其中 σ\sigma 为常数，则 dω=ds/jd\omega=ds/j ,代入上两式可以得到。

双边拉普拉斯正变换

Fb(s)=∫−∞∞f(t)e−stdtF_{b}(s)=\int_{-∞}^{∞}f(t)e^{-st}dt

双边拉普拉斯逆变换

f(t)=(∫σ−j∞σ+j∞(Fb(s)est))/2πjf(t)=(\int_{\sigma-j∞}^{\sigma+j∞}(F_{b}(s)e^{st}))/2\pi j

Fb(s)F_{b}(s) 称为 f(t)f(t) 的双边拉普拉斯变换（或象函数）

f(t)f(t)称为Fb(s)F_{b}(s)的双边拉普拉斯逆变换（或原函数）

2、收敛域

只有选择合适的σ\sigma值才能使积分收敛，信号f(t)f(t)的双边拉普拉斯变换存在。使得f(t)f(t)的拉氏变换存在σ\sigma的的取值范围称为Fb(s)F_{b}(s)的收敛域。

1）对于双边拉普拉斯变换而言，Fb(s)F_{b}(s)和收敛域一起，可以唯一地确定f(t)f(t)。即：

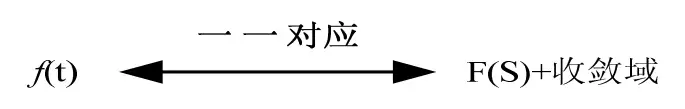
2）收敛域：

部分s平面收敛整个s平面收敛整个s平面均不收敛

3）不同地信号可以有相同的Fb(s)F_{b}(s)，但他们的收敛域不同；不同信号如果有相同的收敛域，则他们的Fb(s)F_{b}(s)必然不同

3、单边拉普拉斯变换

单边拉普拉斯正变换

Fb(s)=∫0−∞f(t)e−stdtF_{b}(s)=\int_{0-}^{∞}f(t)e^{-st}dt

单边拉普拉斯逆变换

f(t)=[∫σ−j∞σ+j∞(Fb(s)est)]ε(t)/2πjf(t)=[\int_{\sigma-j∞}^{\sigma+j∞}(F_{b}(s)e^{st})]\varepsilon (t)/2\pi j

4、常见的拉普拉斯变换对

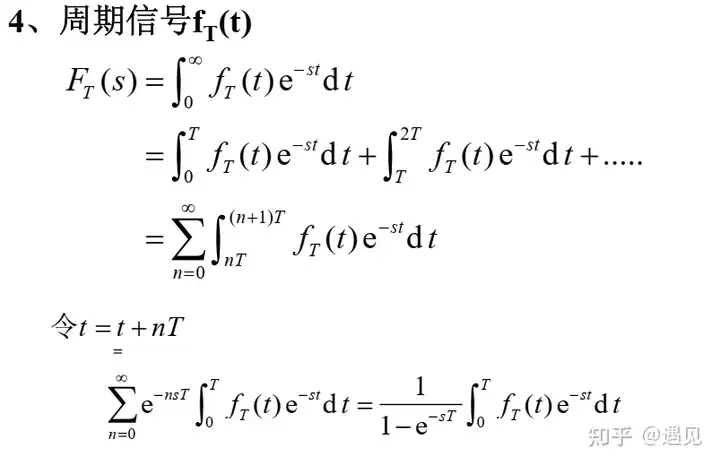
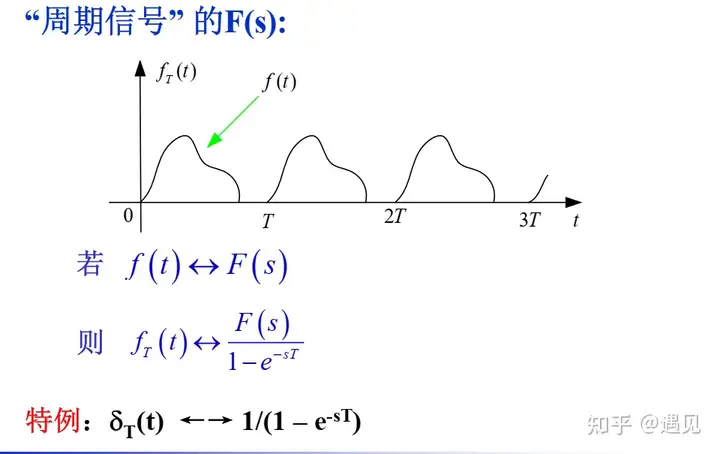
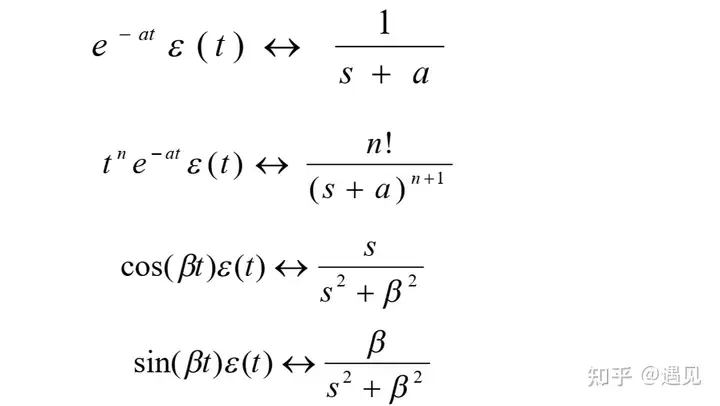
5、拉普拉斯变换的性质

6、拉普拉斯逆变换

常用的方法

1、查表法

2、利用性质

3、部分分式展开

若象函数F(s)是s的有理分式， 可写为：

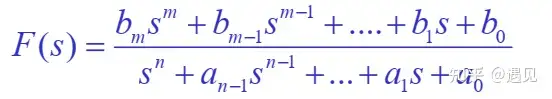
若 m≥nm\geq n (假分式)，可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。

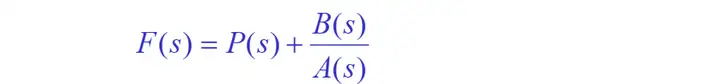
若 m<nm<n （真分式）

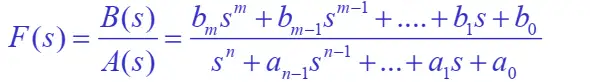
式中A(s)称为系统的特征多项式，方程A(s)=0称为特征方程，他的根称为特征根，也称为系统的固有频率。n个特征根 pip_{i} 称为F(s)的极点

1）F(s)为单极点（单根）

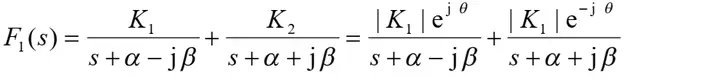
2）F(s)有重极点（重根）