丈量世间万象的数学密钥 —— 定积分的智慧与妙用

古人观天象、测田亩，早已在实践中摸索着量化世间万物的方法。从《九章算术》中 “方田” 篇计算土地面积的出入相补之术，到祖冲之父子推算球体积的 “祖暅原理”，这些古老的数学智慧，实则暗含着定积分思想的萌芽。定积分作为高等数学的重要分支，并非象牙塔中遥不可及的理论，而是贯穿于生产生活、科学研究诸多领域的实用工具。它如同一把精密的尺子，能丈量曲线围成的面积，计算不规则物体的体积，甚至捕捉运动过程中的变化规律，将看似复杂无序的问题，转化为可计算、可分析的数学模型。

在日常生活中，定积分的应用远比想象中普遍。譬如农民估算粮囤中谷物的总量时，若粮囤呈圆台状，直接计算体积存在难度，此时便可借助定积分的思想：将粮囤沿高度方向分割成无数个薄圆台，每个薄圆台近似看作圆柱体，先算出单个薄圆柱体的体积，再将所有薄圆柱体的体积累加，最终得到粮囤的总体积。又如建筑工人设计弧形拱桥时，需要计算拱圈的受力情况，这就需要先确定拱圈曲线与水平方向围成的面积，而定积分正是求解这类不规则图形面积的有力工具。无论是计算水库的蓄水量，还是确定油罐车的容积，定积分都在默默发挥着作用，将抽象的数学逻辑与具体的现实需求紧密相连。

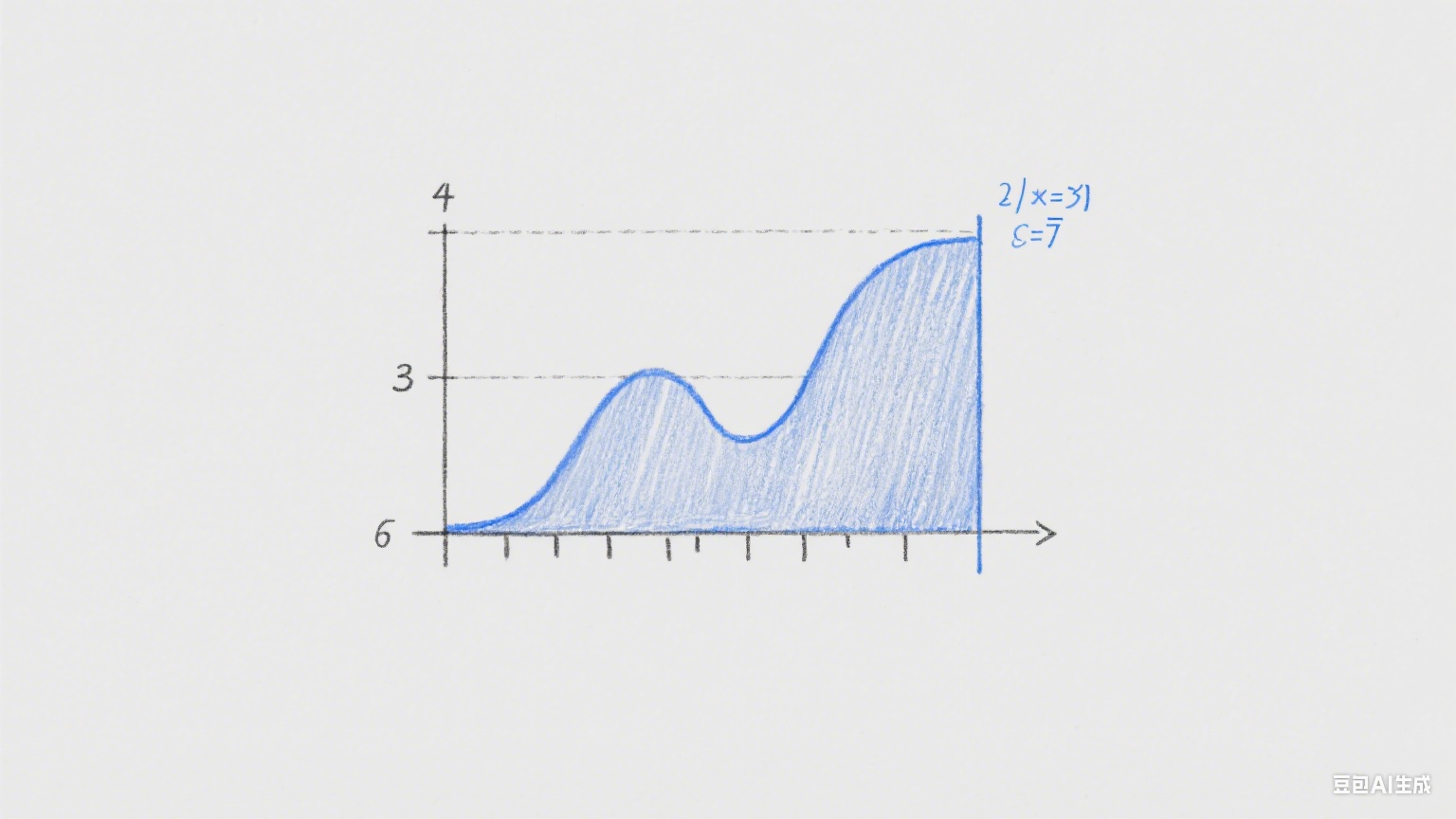
要真正理解定积分的本质，需从其数学定义入手。定积分的核心思想可概括为 “分割、近似、求和、取极限” 四步。以计算平面直角坐标系中，由函数\( y = f(x) \)、x 轴以及直线\( x = a \)、\( x = b \)围成的曲边梯形面积为例：首先，将区间\([a, b]\)任意分割成\( n \)个小区间，每个小区间的长度记为\( \Delta x_i \)（\( i = 1, 2, \dots, n \)）；接着，在每个小区间内任取一点\( \xi_i \)，以\( f(\xi_i) \)为高、\( \Delta x_i \)为底作小矩形，用小矩形的面积\( f(\xi_i) \Delta x_i \)近似代替对应小曲边梯形的面积；然后，将所有小矩形的面积相加，得到和式\( S_n = \sum_{i=1}^n f(\xi_i) \Delta x_i \)，这个和式称为 “黎曼和”；最后，当分割的区间数\( n \)无限增多，且每个小区间的长度\( \Delta x_i \)都趋近于 0 时，若黎曼和\( S_n \)的极限存在，则这个极限值就是函数\( f(x) \)在区间\([a, b]\)上的定积分，记为\( \int_a^b f(x) dx \)，而该极限值也恰好等于曲边梯形的面积。

定积分的计算并非只能依赖定义中的极限方法，牛顿 – 莱布尼茨公式的出现，为定积分的求解提供了极大便利，也让微积分的理论体系更加完善。牛顿 – 莱布尼茨公式指出：若函数\( f(x) \)在区间\([a, b]\)上连续，且\( F(x) \)是\( f(x) \)在该区间上的一个原函数（即\( F'(x) = f(x) \)），则\( \int_a^b f(x) dx = F(b) – F(a) \)。这一公式巧妙地将定积分与不定积分（求原函数）联系起来，使得人们无需再通过复杂的黎曼和极限计算定积分，只需找到被积函数的原函数，再代入上下限求差值即可。例如，计算\( \int_0^1 x^2 dx \)，由于\( \frac{1}{3}x^3 \)是\( x^2 \)的一个原函数，根据牛顿 – 莱布尼茨公式，可得\( \int_0^1 x^2 dx = \frac{1}{3} \times 1^3 – \frac{1}{3} \times 0^3 = \frac{1}{3} \)。这一公式的诞生，不仅简化了计算过程，更深刻揭示了导数与积分之间的互逆关系，成为连接微分学与积分学的桥梁。

在物理学领域，定积分的应用更是不可或缺。以变速直线运动为例，若已知物体的速度函数\( v(t) \)，要计算物体在时间段\([t_1, t_2]\)内经过的位移，就可利用定积分求解。因为速度是位移对时间的导数，即\( v(t) = s'(t) \)（其中\( s(t) \)为位移函数），根据牛顿 – 莱布尼茨公式，位移\( s = \int_{t_1}^{t_2} v(t) dt = s(t_2) – s(t_1) \)。例如，某物体做变速直线运动，速度函数为\( v(t) = 2t + 1 \)（单位：m/s），则该物体在\( t = 1s \)到\( t = 3s \)内的位移为\( \int_1^3 (2t + 1) dt = (t^2 + t) \big|_1^3 = (9 + 3) – (1 + 1) = 10m \)。此外，在计算变力做功、电场强度、引力势能等物理问题时，定积分都发挥着关键作用，它能将变力分解为无数个恒力，将复杂的物理过程拆解为无数个微小的简单过程，再通过求和与取极限，得到最终的物理量。

在工程技术领域，定积分同样有着广泛的应用。机械设计中，工程师需要计算旋转体的体积与表面积，以确定零件的材料用量和结构强度。例如，将平面曲线\( y = f(x) \)（\( x \in [a, b] \)）绕 x 轴旋转一周，形成的旋转体体积可通过定积分计算：\( V = \pi \int_a^b [f(x)]^2 dx \)，表面积则为\( S = 2\pi \int_a^b f(x) \sqrt{1 + [f'(x)]^2} dx \)。在水利工程中，设计拦河大坝时，需要计算坝体受到的水压力，水压力随深度变化而变化（深度越深，压强越大），此时需将坝体沿深度方向分割成无数个小矩形，计算每个小矩形受到的压力，再通过定积分求和，得到坝体受到的总压力。这些实例都表明，定积分是工程技术人员解决实际问题的重要数学工具，它能将工程中的复杂计算转化为严谨的数学运算，确保设计的准确性与安全性。

定积分的思想不仅局限于数学与自然科学领域，在经济学、医学等社会科学领域也有着独特的价值。在经济学中，边际成本函数是总成本函数的导数，若已知边际成本函数\( C'(q) \)（其中\( q \)为产量），则产量从\( q_1 \)增加到\( q_2 \)时，总成本的增量为\( \Delta C = \int_{q_1}^{q_2} C'(q) dq \)；同样，边际收益函数是总收益函数的导数，通过定积分可计算产量变化带来的总收益变化。在医学领域，医生通过监测患者体内药物浓度随时间的变化曲线，利用定积分计算一定时间段内药物在体内的总浓度（即药时曲线下面积 AUC），以此评估药物的吸收、分布、代谢和排泄情况，为临床用药剂量的调整提供依据。这些应用充分展现了定积分的跨学科价值，它如同一条纽带，将不同领域的问题串联起来，用统一的数学语言进行描述和求解。

从古代数学家对图形面积、体积的探索，到现代科学技术中对复杂问题的精准计算，定积分的思想不断发展完善，成为人类认识世界、改造世界的重要工具。它不仅是一门严谨的数学理论，更是一种解决问题的思维方式 —— 通过分割将复杂问题简化，通过近似与求和逼近真实结果，通过取极限追求精确答案。在未来，随着科技的不断进步，定积分必将在更多新兴领域发挥作用，无论是人工智能中数据的积分运算，还是航空航天中轨道的精确计算，都离不开定积分的支撑。那么，当我们面对更多未知的复杂问题时，定积分还能衍生出哪些新的应用形式，又能与其他学科碰撞出怎样的智慧火花呢？这值得每一位学习者和探索者不断思考与实践。