线性代数基础知识大全_线性代数知识点归纳与梳理文库

1.线性代数基础知识总结

方阵的行列式方阵的行列式记作 |A|\left| A \right| 或 detAdetA 方阵A的行列式 |A|\left| A \right| 满足以下的运算规律（设 AA ， BB 为n阶方阵，k为常数）：。

2.线性代数基本知识点总结

（1） |AT|=[A]\left| A^{T} \right|=\left[ A \right]（2） |kA|=kn|A|\left| kA \right|=k^{n}\left| A \right|

3.线性代数详细知识点

（3） |AB|=|A||B|\left| AB \right|=\left| A \right|\left| B \right|矩阵的行列式的值代表矩阵的体积行列式的计算：（1）对角线法则：\ - /（懂的都懂）。

4.线性代数基本知识

（2）沙路法则：矩阵运算（1） A+B=B+AA+B=B+A（2） A(BC)=(AB)CA(BC)=(AB)C（3） (A+B)C=AC+BC(A+B)C=AC+BC（4） C(A+B)=CA+CBC(A+B)=CA+CB

5.线性代数知识点及典型题解析

两个矩阵可以相乘，左边矩阵的列数需要等于右边矩阵的行数正交矩阵若n阶方阵 AA 满足 ATA=EA^{T}A=E ，则称 AA 为正交矩阵，简称正交阵正交矩阵有一下几个重要性质：（1） AT=A−1A^{T}=A^{-1}

6.线性代数知识要点及方法

，即 ATA=AAT=EA^{T}A=AA^{T}=E ；（2）若 AA 是正交矩阵， ATA^{T} （或 A−1A^{-1} ）也是正交矩阵；（3）两个正交矩阵之积仍是正交矩阵；（4）正交矩阵的行列式等于1或-1；

7.线性代数知识点归纳总结

矩阵的秩秩的求法利用矩阵的初等变换，把能转为0的转换为0有多少行非0的秩就为几设 AA 为 m×nm\times n 的矩阵，则矩阵 AA 的秩等于它的列向量组的秩，也等于它的行向量组的秩伴随矩阵行列式

8.线性代数基本知识点

|A|\left| A \right| 的各个元素的代数余子式 AijA_{ij} 所构成的矩阵 A∗=[aij]A^{*}=\left[ a_{ij} \right] 称为 AA 的伴随矩阵矩阵的逆n阶矩阵

9.线性代数知识点总结知乎

AA 可逆的充分必要条件是其行列式 |A|\left| A \right| 不等于0（等于0则矩阵为奇异矩阵），如果一个矩阵可逆，则：A−1=1[A]A∗A^{-1}=\frac{1}{\left[ A \right]}A^{*}

10.线性代数知识汇总

矩阵的转置满足以下(AB)T=BTAT(AB)^{T}=B^{T}A^{T}矩阵的特征值和特征向量

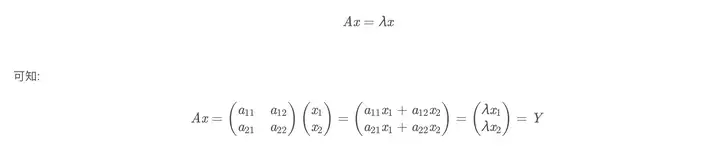
如果满足上公式，向量 xx 是矩阵 AA 的特征向量， λ\lambda 是矩阵 AA 的一个特征值几何上，可以理解为，向量 xx 经过矩阵 AA 的线性变化后，是向量 xx 乘以某个常数的向量，也就是说 。

λ\lambda 浓缩了矩阵 AA 在向量 xx 上投影的信息量，而某一特征值除以所有特征值的和的值就为：该特征向量的方差贡献率（方差贡献率代表了该维度下蕴含的信息量的比例）定理1n阶矩阵 AA 的互不相等的特征值 。

，，λ1，...，λm\lambda_{1}，...，\lambda_{m} 对应的特征向量 ，，p1，...，pmp_{1}，...，p_{m} 线性无关引用《线性代数的几何意义》的描述：“矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。

在这个变换的过程中，原向量主要发生旋转、伸缩的变化如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值”对于实对称矩阵来说，不同特征值对应的特征向量必定正交;我们也可以说，一个变换矩阵的所有特征向量组成了这个变换矩阵的一组基。

矩阵的迹矩阵的迹等于特征值的和。n阶矩阵 AA 的互不相等的特征值 对应的特征向量 线性无关齐次方程组左端没有常数项，右端的值都等于0，这个方程组就是齐次方程。未完待续……