线性代数极简入门_线性代数最简式的定义

 

1.线性代数 最简形

引言本文试图用一万字左右的篇幅直观地讲解线性代数的核心知识Markdown编写，建议开启目录功能安利Smart TOC.作者不是数学专业，学习线性代数是为了用，所以不纠结于细节或高深的证明本文希望能通过给小白读者讲清楚线性代数的核心概念，达到对近期所学知识的一个系统总结。

2.线性代数最简式技巧

欢迎拍砖提醒：本文大量引用马同学的线代内容及图片，只是尽量把知识压缩到一篇文章中，以便理清主线和掌握核心内容想靠本文学好线代是不可能的，吐血建议购买马同学的付费课程复习：向量回忆高中数学向量，就是有方向的量。

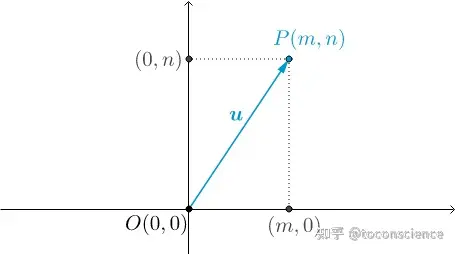
3.线代最简型

如上的二维向量在代数上可以用2个维度上的分量表示： (m,n)\left( m, n \right) 同理，找 nn 个数写到括号里，就构成了一个 nn 维向量三维以内的向量可以用几何表示，可以直观地理解。

4.线代行最简式

现实中大部分问题其实是更高维度的向量，它们无法用几何表示，但性质是相同的一言以蔽之，几何是低维的代数，代数是高维的几何向量加法：利用三角形法则

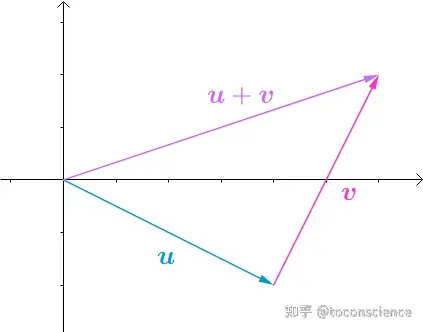
5.线性代数什么叫行最简

在代数上表示，就是分量分别相加。这个性质通过简单的平移可以看出。

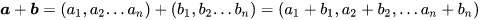
6.线性代数行最简式答案唯一吗

向量点积：

7.简单的线性代数

点积的几何意义是投影后的模长乘积。它其实也能用矩阵解释。向量的长度：

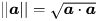
8.线性代数最简行列式

向量的夹角：

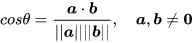
9.线性代数最简式怎么化

来点大学的向量空间：我们可能也发现了，向量是个有方向有长度的箭头，那么它肯定存在于某个空间中。直观来说，二维向量就在二维空间中，三维向量就在三维空间中……

10.线性代数行最简式

而其实我们研究的线性代数，它对向量空间的定义突出一个“线性”：向量空间 VV 是一个集合，其元素是向量该集合对于其元素向量的加法及数乘两种运算封闭即：若则若a∈V,b∈V,则a+b∈V若 \textbf{a} \in V, \textbf{b} \in V, 则 \textbf{a} + \textbf{b} \in V。

若则若a∈V,k∈R,则ka∈V若 \textbf{a} \in V, k \in R, 则 k\textbf{a} \in V你可能不知道，向量空间又叫线性空间向量空间并不一定是 RnR^{n} ，也可以是它们的子集。

下面几个空间也是向量空间：

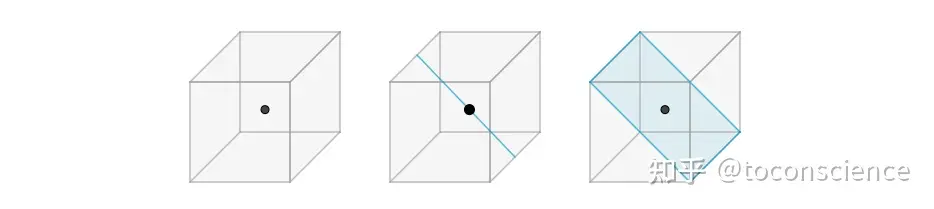
向量组：就是 VV 中的一组向量显然，它们是同维度的向量组合：对 VV 中的一组向量 v1,v2,...vmv_{1},v_{2},...v_{m} ，指定一组实数 k1,k2,...kmk_{1}, k_{2}, ... k_{m}。

, 那么向量b=k1a1+k2a2+...+kmamb = k_{1}a_{1} + k_{2}a_{2} + ... + k_{m}a_{m} 称为该向量组的线性组合，或者说 bb 能被这组向量线性表示。

举个例子：对于 RGBRGB 这三个向量：

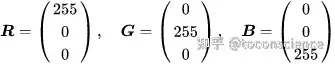
那么黄色就是 RGBRGB 的线性组合：

线性相关与线性无关：向量组中的任一向量都不能被其它向量线性表示，就说向量组线性无关；否则就是线性相关再举个例子： {R,G,B}\{R, G, B\} 是线性无关的， 黄{R,G,B,黄}\{R, G, B, 黄\}。

是线性相关的张成空间：一个向量组 {v1,v2,...vm}\{v_{1},v_{2},...v_{m}\} 的所有线性组合构成的集合 VV （显然是个向量空间），称为该向量组的张成空间，记为 spa

n(v1,v2,...vm)span(v_{1},v_{2},...v_{m}) . 或称该向量组张成 VV 。

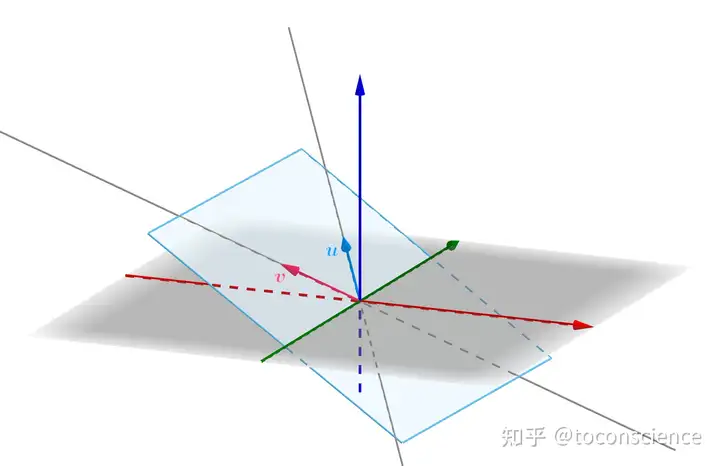
{u,v}张成蓝色的空间向量空间的基：如果一个线性无关的向量组 A={a1,a2,...,an}A = \{ a_{1}, a_{2},..., a_{n}\} 张成向量空间 VV ，则称向量组 AA 是空间

VV 的一个基。基有这么个性质： VV 中的任何向量 xx 都可被唯一地表示为：

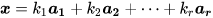
其中 （（k1,k2,...kr)（k_{1}, k_{2}, ... k_{r}) 就相当于 xx 在这组基中的坐标。如果 AA 是标准基（或自然基），其实就变成直角坐标系了。

向量空间的维度：就是一组基的向量个数。矩阵：从线性方程组说起矩阵的引入矩阵是英国数学家阿瑟·凯莱（1821－1895）为了研究线性方程组而发明的。他发现，对于这样的线性方程组：

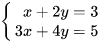
未知数的名字 xx 、 yy 根本不重要，可以直接把系数提出来，用一种阵列（称为矩阵）的方式表示，就称为系数矩阵：

如果把等号右边的数字也提出来，就叫做增广矩阵：

要解方程组，其实就是用高斯消元法，逐次迭代，将方程组化为简单形式：

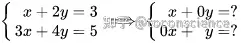
如果用 r1r_{1} 表示第一行， r2r_{2} 表示第二行； r1′r_{1}^{} 表示新的第一行， r2′r_{2}^{} 表示新的第二行，那么整个过程如下：

那么怎么能简洁地表示高斯消元法呢？前面我们已经用增广矩阵来表示过方程组了，上面的第一步可以表示成：

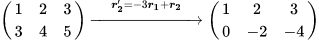
中间的这个变换过程：r1′=1r1+0r2r2′=−3r1+1r2r_{1}^{} = 1r_{1} + 0r_{2}\\ r_{2}^{} = -3r_{1} + 1r_{2}干脆写成另一个矩阵得了：

(10−31)\begin{pmatrix} 1 & 0 \\ -3 & 1 \end{pmatrix}那么我们规定矩阵的单行乘法是这样：

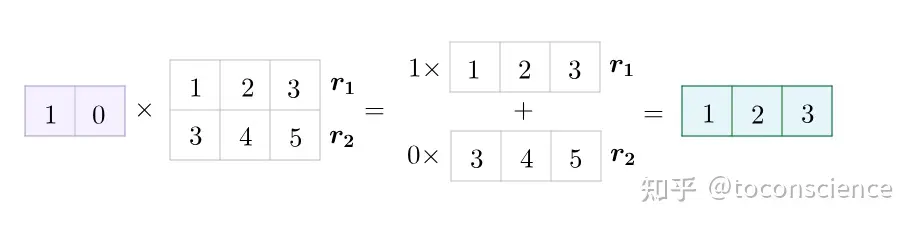
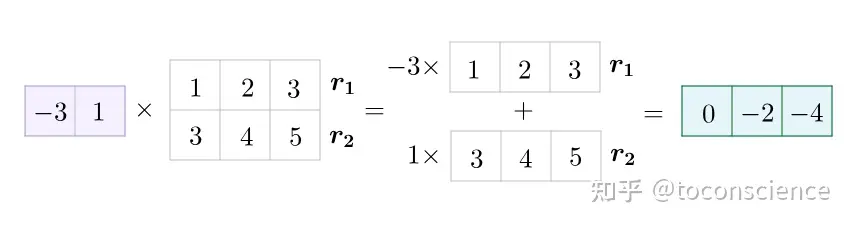
多行乘法，就是单行分别乘，然后放一起：

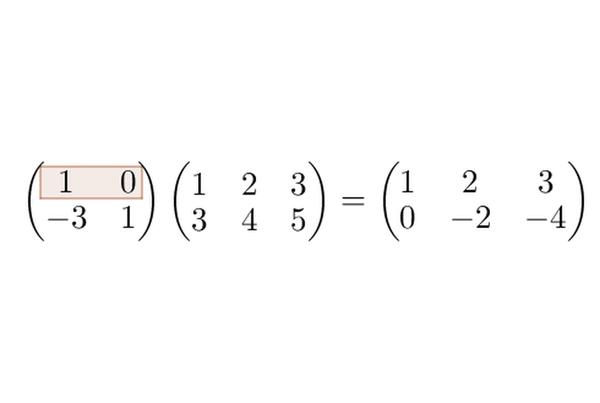
啊哈！现在终于可以用矩阵乘法来表示高斯消元的过程了：

整个过程最终可简化为：

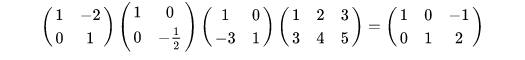
更详细的讲解，请参阅从高斯消元法到矩阵乘法初等行变换和初等行矩阵由矩阵乘法规律可知，如果一个矩阵是方阵，并且只有对角线上的元素是1，其它元素都是0，那么它乘以任何矩阵的结果都是原矩阵这就是单位阵II ，

IA=AIA = A 。

高斯消元法用矩阵来理解的话，可以归纳为3种基本的行变换，称为“初等行变换”。在单位阵上应用其中一种变换一次得到的矩阵，就是“初等行矩阵”。

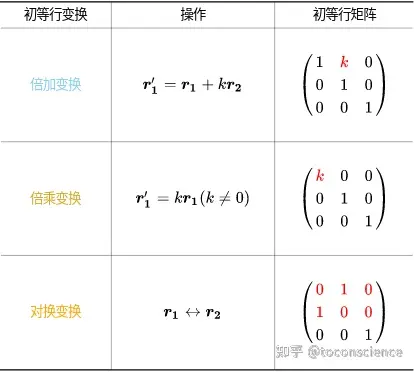
那么初等行矩阵有什么用呢？初等行矩阵乘上矩阵 AA ，就相当于在矩阵 AA 上实施了对应的初等行变换比如上面的初等行矩阵 (10−31)\begin{pmatrix} 1 & 0 \\ -3 & 1 \end{pmatrix}。

，就是单位阵应用了倍加变换 r2′=−3r1+1r2r_{2}^{} = -3r_{1} + 1r_{2} 得到的，而它乘上矩阵 AA 的效果，就是对 AA 实施了倍加变换 r2′=−3r1+1r2r_{2}^{} = -3r_{1} + 1r_{2}

：

矩阵乘法的几种视角行视角：上面矩阵乘法的定义就是行视角。

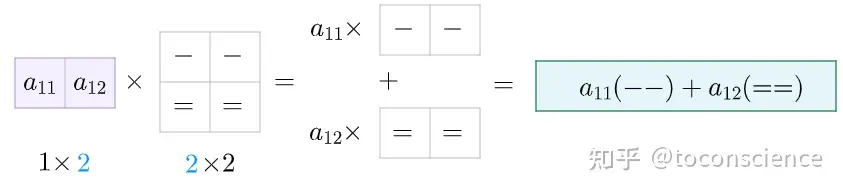
适用场景：行向量（可理解为单行矩阵）乘以矩阵。

列视角：通过行视角可以推出列视角（两者为何等价不作证明）：

适用场景：矩阵乘以列向量（可理解为单列矩阵）。

点积视角（教科书定义）：对于矩阵 A=(aij),B=(bij)A =(a_{ij}), B = (b_{ij}) ，AB的乘积 C=(cij)C = (c_{ij}) 满足：

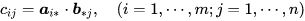
这个定义实在是难以理解其意义，只适合用来计算和死记硬背。现在你明白高数教的都是啥了吧！基变换视角：举个例子：矩阵 AA 乘以向量 a\textbf{a} 得到向量 b\textbf{b}

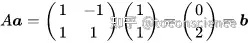
而矩阵 AA 的列向量是

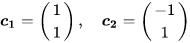
按照矩阵乘法的列视角，

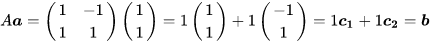
这说明，矩阵乘法的结果可以理解为，原来的向量 a\textbf{a} 的系数（坐标）不用变，只是把基向量从自然基变成了矩阵 AA 的列向量！

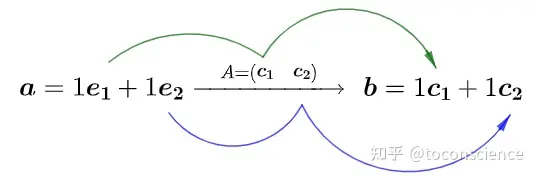
或者说，输出向量 b\textbf{b} 是矩阵 AA 的列向量的线性组合。妙啊！

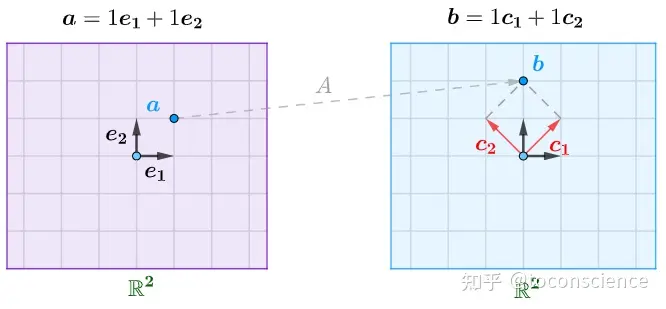
把系数用 x1,x2x_{1}, x_{2} 代替，就得到一般的结论：

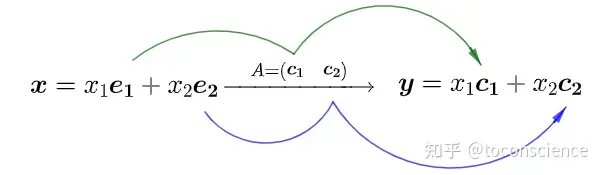
当然，我们知道行视角和列视角是等价的，取决于你是横着看还是竖着看，所以上面的讨论在行视角下也成立。

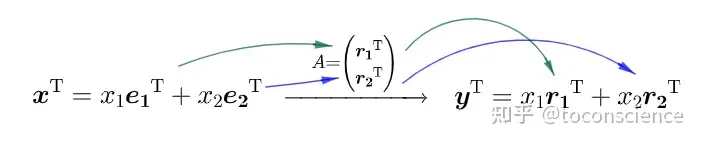
更详细的解释，参见：马同学：线性代数（二）如何理解矩阵乘法 以及 异色瞳哥的经典视频从函数（映射）角度来理解线性方程组的解逆矩阵其实，可以把矩阵当作函数来研究因为函数，变换，映射这些都是一个意思而矩阵的作用就是把一个向量映射成另一个向量，所以当然可以看成映射！。

其实矩阵还是线性映射，而从线性映射出发又可以得到矩阵的另一个著名的定义。这一部分很不直观，我们还是选择线性方程组的角度吧！关于线性映射的简单推导可以看看这篇。

如图所示， A\textbf{x} =\textbf{y} 可以看成函数，它的定义域是个向量空间，值域也是个向量空间。为啥非得研究函数呢？看这个图：

因为任何的线性方程组可以写成 A\textbf{x} =\textbf{y} ，那要求方程组的解，也就是 \textbf{x} ，简单来说不就是把 A 除过去完了？（等等，你不是说 A 是个函数吗？那不应该是除啊，应该是求

A 的反函数啊？你说的对，我草率了…… 准确地说，是我们只要找到 A 的反函数，然后对等式两边再应用一次反函数，就能得到 \textbf{x} 了）那么假设有另一个矩阵，叫 A^{-1} ，它和 A 的乘积就是单位阵

I 那我们给函数的两边都乘上 A^{-1} ，就得到 \textbf{x} =A^{-1}\textbf{y} ，求解完成！这个 A^{-1} 就是矩阵 A 的逆矩阵，相当于逆映射，反函数而到这里，解线性方程组就变成了求解系数矩阵的逆矩阵

，妙啊！重所周知，不是所有函数都有反函数啊！所以矩阵也不是都有逆矩阵。So，我们就来研究如何判定矩阵有没有逆矩阵。矩阵的秩我们可以用韦恩图这个神器来考察矩阵：

对于列向量矩阵函数：

它的函数四要素是：

画成韦恩图就是：

再进一步，矩阵 A 的所有列向量组成的向量组称为矩阵的列向量组而列向量组张成的空间称为列空间，记作 colsp(A) . 很显然，如果定义域是自然定义域，按照上一节矩阵乘法的基变换视角，那么值域 Ax 就等于列空间：

列空间的维度称为列秩 （rank ）。如果维度等于列的个数，也就是列向量组线性无关，就称为列满秩。所以更新一下，在自然定义域下， m\times n 的列向量矩阵函数 Ax=y 的四要素为：

同理，换成行视角看， m\times n 的行向量矩阵函数 x^{T}A = y^{T} 的四要素为：

接下来，考虑单射：所谓单射就是每个 y 最有有一个 x 与之对应对于线性映射来说，可以推导出：矩阵函数是单射\Leftrightarrow 定义域的维度 = 值域的维度而对 m\times n 矩阵来说，定义域维度是 。

n ，值域的维度即列秩，而矩阵的列向量只有 n 个，所以：矩阵是列满秩。再推广到行向量矩阵，可以得到：

其实，可以证明，任意矩阵的行秩都等于列秩（证明略）所以矩阵 A 的秩的定义就是行秩或者列秩记为 rank(A) 由这个定理，我们就又能愉快地讨论满射了：所谓满射就是值域与到达域相等对于列向量矩阵来说就是：。

同理，推广到列向量矩阵：

最后的双射就简单了：

那么矩阵的秩到底有什么意义呢？因为矩阵的秩就是矩阵函数的值域的维度，所以秩越大，值域的维度越大，反之亦然所以可以把秩想象成一个筛子（而复合矩阵，就是筛子的叠加）详细的讲解参见 如何通俗理解矩阵的秩？到这里，我们终于可以给出逆矩阵的定义了：

其中 A 只能是双射、满秩方阵。可逆等价于满秩。而逆矩阵怎么求，其实上一章的初等行变换求解线性方程组已经给出了思路：

先通过一系列的初等行变换，将矩阵 A 变成单位阵 I再把这些初等行矩阵相乘，就能得到逆矩阵 A^{-1}然而大佬就是大佬，数学家们还是嫌这样太麻烦，表示可以两步合成一步：把矩阵 A 和单位阵 I 合成一个矩阵

(A|I) ，然后对这个矩阵进行初等行变换。把左边变成单位阵之后，右边的就是逆矩阵 A^{-1} ：

这就是高斯若尔当法如何求矩阵的秩：我们已经知道所有的初等行矩阵和初等列矩阵都是满秩矩阵，所以它们和矩阵 A 相乘不改变 A 的维度所以求矩阵 A 的秩就简单了：对矩阵应用各种初等行变换和初等列变换，直到化简成行阶梯型、行最简形、甚至标准型矩阵，矩阵中不全为0的部分就是矩阵的秩了。

线性方程组的解终于又说回线性方程组了我们已经知道，方程组可以写成 A\textbf{x} =\textbf{b} 的形式解的存在性：如果有解，说明 \textbf{b} 在 A\textbf{x} 的值域中。

也就是说 \textbf{b} 可以被 A 的列向量组线性表示，也就是说把 \textbf{b} 和 A 拼起来写成增广矩阵 B = (A|\textbf{b}) 的话， rank(A) = rank(B)

；如果无解，则 \textbf{b} 和 A 的列向量组线性无关，所以 rank(A) < rank(B) 特别地，如果 A 是行满秩，那不用麻烦了，此时值域等于到达域， \textbf{b} 一定在值域中，所以一定有解。

解的个数：解是不是唯一的，等价于矩阵 A 是不是单射所以：唯一解，当且仅当是 A 是列满秩无数解，当且仅当 A 不是列满秩最后再来个特例， A 是满秩矩阵则一定有且只有一个解如何求解集：如果 \textbf{b} = \textbf{0}。

，则称为齐次线性方程组（否则就是非齐次）此时的解集称为零空间（又名核空间），记为 null(A) 那么如果 \textbf{b} \ne \textbf{0} ，我们可以先求出 null(A) ，然后再求出一个特解 。

\textbf{p} ,最终的解集就是零空间再加上 \textbf{p} 的平移： \textbf{p} + null(A)

求 null(A) 的过程基本就是高斯消元法，这里省略线性代数基本定理对于 m\times n 矩阵 A 构成的矩阵函数，其定义域是 n 维的，而值域的维度是 rank(A) 如果 rank(A) < n。

，那其余的维度跑哪去了呢？直观地说，就是跑到零空间去了所以线性代数基本定理是说：rank(null(A)) + rank(A) = n一鱼两吃：行列式行列式的来历对于上面的线性方程组，（矩阵满秩时）其实是能够直接给出解的公式的：。

对于二元一次线性方程组：

解为：

好像有点规律？于是数学家就规定（对角线法则）：

于是解可以简化成：

同样对于三元一次线性方程组：

解为：

同样规定一种运算：

那么刚才的解可以化简为：

克拉默就发现，只要定义好了行列式，那么线性方程组的解就是可以直接写出来的：

分母都是系数矩阵的行列式分子是将系数矩阵的第 i 列换成 \textbf{b}最后， n 阶行列式的定义为：

值为：

也就是说，最终的值是一个求和，其中每一项都是一组乘积角标第一项都是 1,2,…,n ,而第二项的 p_{1},p_{2},...,p_{n} 表示 1,2,…,n 的全排列 t 就表示某一组排列的逆序数。

这个定义不需要强记，我们后面来讨论它的意义及性质实在好奇，可以看看马同学：线性代数（三）行列式的来历行列式的几何意义先看二阶方阵 A_{2}=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}。

，它的列向量记为 \textbf{c}_{1}、\textbf{c}_{2} ，由矩阵乘法的基变换视角，相当于 R^{2} 平面的自然基被映射成了 \textbf{c}_{1}、\textbf{c}_{2}

：

画成图像就是正方形映射成了平行四边形：

可以证明： \textbf{c}_{1}、\textbf{c}_{2} 围成的平行四边形面积就是二阶行列式 |A_{2}| :

那么 |A_{2}| 显然还可能小于 0 ，它表示什么呢？其实就是把 \textbf{c}_{1}、\textbf{c}_{2} 翻转过来：

所以严格地说，二阶行列式 |A_{2}| 表示 \textbf{c}_{1}、\textbf{c}_{2} 围成的平行四边形的有向面积又由于映射之前，自然基围成的正方形的面积是 1 ，所以二阶行列式还表示有向面积的。

伸缩比例！有了二阶行列式，我们自然地可以推广到三阶：

三阶行列式 |A_{3}| 表示 \textbf{c}_{1}、\textbf{c}_{2}、\textbf{c}_{3} 围成的平行六面体的有向体积同样还表示有向体积的伸缩比例另外，如果把自然基向量也写进行列式，它还能表示。

向量叉积，太有意思了！

叉积的定义就是有方向的面积，也就是说还是个向量： \textbf{S} = \textbf{b} \times \textbf{c}

法线的方向则是右手定则：

对于二阶方阵，列向量的叉积就是矩阵的行列式。行列式的性质余子式：就是在把 a_{ij} 所在的行和列划掉后剩下的部分，记作 M_{ij}

代数余子式：就是给余子式加上正负号。 A_{ij} = (-1)^{i+j}M_{ij}

拉普拉斯展开：可以证明，行列式的值等于某行（或某列）的元素与其代数余子式乘积之和。

行列式与可逆矩阵：其实很好理解，比如二阶矩阵，如果行列式等于0，说明本来的 \textbf{e}_{1}、\textbf{e}_{2} 围成的正方形被映射成了直线或点，显然矩阵不满秩。

初等变换对行列式的影响：再提一些行列式的简单性质：行列式乘以 k 倍，等于某行（列）乘以 k某两行（列）互换后，行列式正负号发生改变将某一行（列）的 k 倍加到另一行（列）里，行列式的值不变如果某一行（列）的每个元素是两数之和，则可拆分为两个相加的行列式

矩阵的乘积对应的行列式等于行列式的乘积。可以理解为两次伸缩。 |AB|=|A||B|伴随矩阵：就是 A 的代数余子式的转置。( C 是 A 的代数余子式矩阵)

矩阵的逆矩阵可以用伴随矩阵求出： A^{-1}=\frac{1}{|A|}A^{*} 哇，逆矩阵还可以这么求！小结到这里，行列式差不多讲完了行列式也是从线性方程组引入的，而线性方程组求解的本质是求逆矩阵。

在上一章中我们的求法是高斯若尔当法，本章则发现通过行列式可以直接求出逆矩阵矩阵的应用基变换同一个向量空间，可以选择不同的基那么同一个点在不同的基下显然会有不同的坐标由于切换基向量而引起的坐标变换，就称为基变换。

由矩阵乘法的基变换视角，只要把矩阵的列视为基向量，就可以计算基变换了。

假如我们知道某向量在一组基 \{\textbf{e}_{1}^{}, \textbf{e}_{2}^{}\} 下的坐标（例如 (-2,0) ），则可以得到其在自然基下的坐标：

坐标下面写基向量代表是在这组基下面的坐标。自然基 e 可以省略。关键就是把 e^{} 转换成 e 的那一步，实现了坐标系的切换，而这一步可以写成矩阵乘法的形式：

其中 P=(\textbf{e}_{1}^{}, \textbf{e}_{2}^{}) ，结果就是：

反过来，通过 P 的逆矩阵可以把自然基中的坐标转换成非自然基的：

P 和 P^{-1} 都称为过渡矩阵。

等价矩阵假设有两个 m\times n 的矩阵 A 和 B 当且仅当存在两个可逆矩阵 P 和 Q 使得： B=PAQ ，此时两者等价记作： A\sim B等价矩阵的意义是不同基下的同一个映射（只是定义中把 。

P^{-1} 写为 P ）：

因为初等变换对应的矩阵都是满秩矩阵，所以变换前后的矩阵是等价矩阵，秩相同，代表的是同一个线性映射对于同型矩阵： A \sim B \Leftrightarrow rank(A) = rank(B)相似矩阵。

：如果B映射两边是同一组基，那么 P 和 Q 其实是互为逆矩阵 B=P^{-1}AP 这种特殊的情况称两者为相似矩阵，A \simeq B.特征值和特征向量对 n 阶方阵 A ，如果存在数 \lambda。

和 n 维非零列向量 \textbf{x} 使得 A \textbf{x} = \lambda \textbf{x} 成立，那么 \lambda 称为矩阵的特征值， \textbf{x} 称为 \lambda

对应的特征向量。特征向量的几何意义是，这些向量在经过矩阵 A 的变换后，方向没有发生变化，只是长度发生了伸缩。

特征值和特征向量如何求呢？根据定义可以得到：

由于 \textbf{x} 必须是非零向量，所以方程必须有非零解，所以矩阵 (A - \lambda I) 必须不是满秩矩阵，即： |A-\lambda I| = 0 ，即：

这个行列式展开是个多项式，因为只有一个 \lambda 变量，所以是个一元 n 次多项式根据代数基本定理：一元 n 次方程在复数范围内正好有 n 个复数根，这 n 个根显然就是 n 阶方阵 A 的特征值。

把特征值代入原式就可以求出对应的特征向量特征值有一些特别的性质可以证明：矩阵的所有特征值的乘积等于矩阵的行列式相似矩阵具有相同的特征值，从而行列式相等矩阵的所有特征值之后等于矩阵的主对角线元素之和，后者称为矩阵的迹，记为 。

tr(A)对角化若 n 阶矩阵 A 有 n 个线性无关的特征向量： \textbf{p}_{1}, \textbf{p}_{2}, ..., \textbf{p}_{n} ，对应的特质值为：

则由特征向量组成的特征矩阵 P 可表示为： P = (\textbf{p}_{1}, \textbf{p}_{2}, ..., \textbf{p}_{n})将 P 作为过渡矩阵可以得到一个相似矩阵 \Lambda = P^{-1}AP

， \Lambda \simeq A ，而 \Lambda 为：

这个把矩阵变换成一个相似的对角矩阵的过程，就称为对角化对角矩阵有很好的性质，它的特征值就是对角线上的元素，而行列式就是这些元素的乘积特征空间：一个特征空间（ eigenspace ）是具有相同特征值的特征向量与一个同维数的零向量的集合。

因为特征向量具有线性的特征，所以我们知道这是个向量空间记为： E_{\lambda} = \{u \in V | Au = \lambda u\}一个矩阵是否可以对角化取决于其特征向量是否线性无关而判断是否线性无关则要使用下面的方法：。

正交化标准正交基与正交矩阵：模长为1，且两两相交的基称为标准正交基显然，标准正交基就是对自然基旋转得到的，它的变换只会旋转，不会形变标准正交基有个很好的性质，某向量在其中一个基上的坐标分量，就是在它上面的投影长度。

也就是点积

由标准正交基构成的方阵就称为正交矩阵。它还有个有趣的性质（转置矩阵等于逆矩阵）： A^TA = I ，即 A^T=A^{-1}显然，正交矩阵的作用是旋转，它可以是其它正交矩阵之间的过渡矩阵。

把非标准正交基变换为标准正交基的过程，称为施密特正交化。方法就是作垂线。

找到标准正交基之后，自然可以得到过渡矩阵，从而实现基变换最后，对于特殊的对称矩阵 A ，它的特征向量是正交的，所以可以同时实现对角化和正交化，这称为可对角正交化， A 称为对角正交矩阵二次型n 元二次齐次函数称为二次型：。

二次型可以写成矩阵的形式：

写成更现代的形式则是：

因此，一个二次型就对应一个对称矩阵。可以通过研究对称矩阵来研究二次型。对于一个二次型，它的矩阵默认是以自然基为基的，因此可以写成：

假设再有一个过渡矩阵 P ，使得: \textbf{x}_{e} = P \textbf{y}_{e^{}} ，代入上式可得：

化简可得：

中间的部分就称为合同矩阵，这个过程相当于给二次型矩阵做了基变换注意它跟相似矩阵实在是太像了，而后者是 P^{-1} ，合同矩阵为 P^T如果二次型只有二次项，则称为标准型其对应的矩阵是个对角矩阵将普通的二次型变换为标准型的过程，就称为

标准化标准化有两种方法，分别是正交标准化和拉格朗日配方法参考资料马同学图解线性代数 ：吐血推荐，并建议入手马同学的所有课程学习曲线极为平坦，并且配有练习题，深得学习规律的精髓异色瞳哥的经典系列：适合入门后再看。

那如何入门呢，建议还是看马同学《程序员的数学3 线性代数》：讲的也很形象了，并补充了计算机要考虑的数值计算内容，缺点是书有点厚极客时间-重学线性代数 ：适合入门后学习，扩展视野《线性代数应该这样学》：是教科书，理论推导很花时间，看了前三章后放弃了。

不过也吸收了不少线性映射的思想接下来我讲讲为啥不推荐拿它入门：在前言中，作者说明了书名的来历“大多数的教材都很早就引入了行列式，用来证明本征值等问题；而行列式既难懂又不直观，而且其定义的引入也往往缺乏动机”。

然而实际上行列式通过方程组的解引入是很自然的，此外还有很多的几何意义相反，书中的线性映射才是相当的不直观啊在前言的致学生一节中，作者提到：你是第二次接触到线性代数…… 你不能像看小说那样去读数学要是你不到一小时就读完一页的话，可能就读的太快了。

啊…… 这确实不是个入门书。结论：学习是个螺旋上升的过程，知识依赖往往是有闭环的（也就是死循环）。有的书适合学会了之后再看，可以深化理解，进入下一个阶段；但入门的时候千万别选择，除非你的时间无限。