【高数笔记】二重积分的计算方法（直角坐标系）_二重积分θ怎么求

 

1.二重积分坐标变换公式

直角坐标系下二重积分的计算方法利用直角坐标系求二重积分时，需要根据积分区域D来选择积分的顺序这里以“X型”为例我们不妨通过一个例题来搞懂二重积分在直角坐标系下的计算例1：计算 ∬Dx2ydσ\iint_Dx^2yd\sigma。

2.二重积分的坐标变换公式

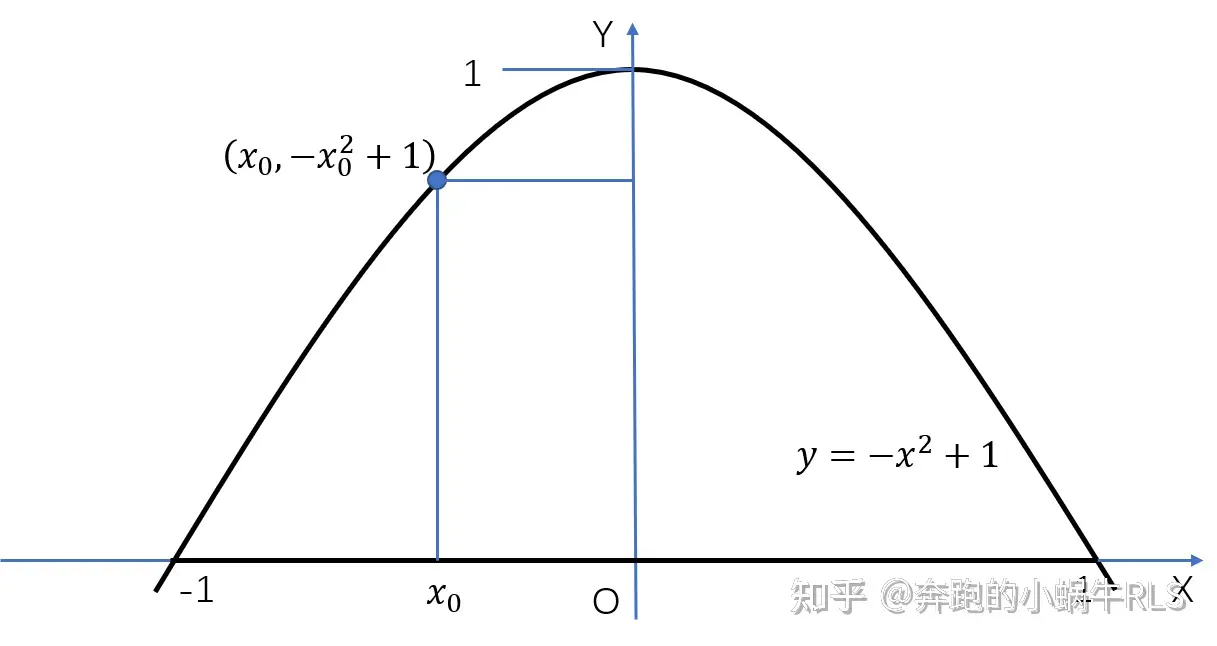
，其中D是由曲线：y=−x2+1y=-x^2+1 与x轴围成的图形。解：我们不妨先画出积分区域。

3.二重积分坐标系转换公式

如果我们用 x=x0x=x_0 这张平面去截被积函数形成的曲面，那么会在这张平面上得到一个关于 yy 的函数图像，y的取值范围是 [0,−x02+1][0,-x_0^2+1] ，其中左端点的0是函数 y

4.二重积分的坐标变换

=0y=0 (x轴)在 x0x_0 处的函数值那么我们可以利用定积分 ∫0−x02+1x02ydy\int_{0}^{-x_0^2+1}x_0^2ydy 计算出这个截面图形的面积如果能让 x0x_0 取遍所有取值范围里的值，再把这些值对应的定积分值加起来，那不就是二重积分的结果了吗。

5.二重积分坐标转换

而这个对和式求极限的过程恰好也是积分的过程所以我们不妨设 x=x0x=x_0 处截面的面积为 A(x)A(x) ，则刚刚的过程可以描述为 V=∫−11A(x)dxV=\int_{-1}^{1}A(x)dx

展开后就是 ∫−11(∫0−x2+1x2ydy)dx\color{red}{\int_{-1}^{1}}(\color{blue}{\int_0^{-x^2+1}x^2ydy})\color{red}{dx}。

.这种积分里面套积分的式子我们称为二次积分，刚刚的式子可以简写为 ∫−11dx∫0−x2+1x2ydy\int_{-1}^1dx\int_0^{-x^2+1}x^2ydy .接下来要做的就是计算这个二次积分了，我们按照从内到外的顺序进行计算。

注意到内层的积分是对y求积分，所以x可以看作是常数所以内层积分的结果就是 x2⋅12(−x2+1)2=12x6−x4+12x2x^2\cdot\frac{1}{2}(-x^2+1)^2=\frac{1}{2}x^6-x^4+\frac{1}{2}x^2。

.那么，这个二次积分就化为了 ∫−1112x6−x4+12x2dx=8105\int_{-1}^1{\frac{1}{2}x^6-x^4+\frac{1}{2}x^2}dx=\frac{8}{105}

.总结一下，求解二重积分 ∬Df(x,y)dσ\iint_Df(x,y)d\sigma 可以简化为如下步骤：①画出积分区域D的图形，找出围成D的上下两条曲线的函数 y=φ1(x),y=φ2(x)y=\varphi_1(x),y=\varphi_2(x)

;②写出自变量的取值范围：x的取值范围由题目决定，不妨先假设为 [a,b][a,b] ；y的取值范围由x决定，具体范围是 [φ2(x),φ1(x)][\varphi_2(x),\varphi_1(x)]

.③将二重积分转换为二次积分，也就是把x看做常数，对y进行积分，然后在对其结果对x积分，即 ∫abdx∫φ2(x)φ1(x)f(x,y)dy\int_a^b dx\int_{\varphi_2(x)}^{\varphi_1(x)}f(x,y)dy

.④计算：选择从内到外进行计算即可，注意，除了积分变量以外的字母都可以看作是常数另一种方式理解积分在开始正题之前，我想先介绍一个概念——遍历所谓遍历，就是按一定的方式访问一个集合中所有的元素记要被遍历的集合为 。

SS ,遍历到的某个元素为 ee ，那么我们不妨记这个遍历的过程为 ∀e,x∈S:...\forall \space e,x\in S:... ，其中x为元素e所在的位置，冒号后面是要对当前的元素如何处置。

如果 SS 中的元素需要两个坐标来定位，那么就记作 ∀e,(x,y)∈S:...\forall \space e,(x,y)\in S:... .我们不妨先从定积分开始说起一个定积分 ∫abf(x)dx

\int_a^bf(x)dx ，实际上是把区间 [a,b][a,b] 分割成了无数份 dxdx ，而积分做的便是把每一份 dxdx 乘以它所在处的函数的值，最后求和如果把这里的数字看作长度，那么定积分求的就是曲线与坐标轴所围成的图形的面积。

我们把它写成“遍历的语言”就是： ∀e,x∈S:A=A+e⋅f(x)\forall \space e,x \in S:A=A+e\cdot f(x) ，其中A初值为0，e就是前面的dx那么我们继续来看二重积分。

首先我们要知道二重积分的积分区域是二维的，如果在里面遍历每一个小的面积元素 dσd\sigma ，是需要两个坐标来定位的，那就是 ∀e,(x,y)∈S:...\forall \space e,(x,y)\in S:...

.不过，对于定积分来说，我们可以知道 f(x)dxf(x)dx 是一个函数的微分，所以我们可以求出它的原函数但是对于一个二维的元素 dσd\sigma 来说，我们并不知道 f(x)dσf(x)d\sigma。

的代数意义不过还好，我们知道“点动成线，线动成面”，所以我们不妨先遍历平面上的每一条线，然后再遍历线上的每一个点，这样就是我们可以解决的问题了我们不妨先假设积分区域D是“X型”的，x的取值范围是 [a

,b][a,b] ，那么二重积分写成遍历的写法就是： ∀l,x∈S:V=V+A,∀e,y∈l:A=A+e⋅f(x)\forall \space l,x \in S: V=V+A\space ,\forall \space e,y \in l: A=A+e\cdot f(x)

.不难发现，内层的遍历实际上就是一个定积分，积分区间是二重积分区域上的某一条线不难发现，此时这条线只能用一个坐标来表达，而在直角坐标系中，这样的线只能是垂直于坐标轴的直线这些直线与被积区域相交的部分就是元素 。

ll .如果假设围成图形的上下边界的曲线为 y=φ1(x)y=\varphi_1(x) 和 y=φ2(x)y=\varphi_2(x) ，那么此时直线 ll 就是区间 [φ2(x),φ1(x)][\varphi_2(x),\varphi_1(x)]

.那么我们用无限小的微元dy遍历元素 ll ，可以得到 ∫lf(x)dy\int_lf(x)dy ，即 ∫φ2(x)φ1(x)f(y)dy\int_{\varphi_2(x)}^{\varphi_1(x)}f(y)dy

.这时候，原来的那个遍历就变成了 ∀l,x∈S:V=V+∫φ2(x)φ1(x)f(y)dy\forall \space l,x \in S: V=V+\int_{\varphi_2(x)}^{\varphi_1(x)}f(y)dy

.现在我们知道 ll 是只需要一个坐标即可确定的直线，那么我们只需要遍历 xx 的取值范围即可，即 ∀x∈[a,b]:V=V+∫φ2(x)φ1(x)f(y)dy\forall \space x \in [a,b]: V=V+\int_{\varphi_2(x)}^{\varphi_1(x)}f(y)dy

，写成积分的形式就是 ∫ab[∫φ2(x)φ1(x)f(y)dy]dx\int_a^b[\int_{\varphi_2(x)}^{\varphi_1(x)}f(y)dy]dx ，也可以简写为 ∫abd

x∫φ2(x)φ1(x)f(x,y)dy\int_a^bdx\int_{\varphi_2(x)}^{\varphi_1(x)}f(x,y)dy注：这里的 dxdx 表示直线元素 ll 有一个无穷小的宽度。

同理，当积分区域D是"Y型"时，换个方向进行遍历即可得出对应的计算公式。三重积分也是同样的道理，这里就不再作说明了。