二重积分的计算 | 直角坐标系下的计算_二重积分计算法

1.二重积分的计算视频

谢邀！二重积分是二元函数在空间上的积分，同定积分类似，是某种特定形式的和的极限本质是求曲顶柱体体积接下去我们将介绍二重积分的计算方法，而本文是针对二重积分在直角坐标系下的计算一、二次积分的XX型和YY型两种计算方法

2.二重积分怎么算dσ

（1）XX型（先YY后XX型）∬Df(x,y)dσ=∫abdx∫φ1(x)φ2(x)f(x,y)dy=∫ab∫φ1(x)φ2(x)f(x,y)dydx\begin{aligned} \iint\limits_{D}^{}f(x, y) d \sigma &=\int_{a}^{b} d x \int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y \\ &=\int_{a}^{b} \int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y d x \end{aligned}

3.二重积分计算法

大致步骤：第一步：先画出积分区域DD的图形，确定xx的积分限；第二步：确定yy的积分限一条平行于yy轴的直线沿yy轴正方向穿过积分区域，穿入线φ1(x)\varphi_{1}(x)为积分下限，穿出线φ2

4.二重积分计算总结

(x)\varphi_{2}(x)为积分上限；第三步：计算重积分计算∫φ1(x)φ2(x)f(x,y)dy\int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y。

5.二重积分的计算过程

，会得到一个关于xx的多项式g(x)g(x)，再计算∫abg(x)dx\int_{a}^{b} g(x) d x得出最后结果（2）YY型（先XX后YY型）∬Df(x,y)dσ=∫cddy∫ϕ1(y)ϕ2

6.二重积分计算视频

(y)f(x,y)dx=∫cd∫ϕ1(y)ϕ2(y)f(x,y)dxdy\begin{aligned} \iint\limits_{D}^{}f(x, y) d \sigma &=\int_{c}^{d} d y \int_{\phi_{1}(y)}^{\phi_{2}(y)} f(x, y) d x \\ &=\int_{c}^{d} \int_{\phi_{1}(y)}^{\phi_{2}(y)} f(x, y) d x d y \end{aligned}

7.二重积分简单计算

大致步骤：第一步：画出积分区域DD的图形，确定yy的积分限；第二步：确定xx的积分限是一条平行于xx轴的直线沿xx轴正方向穿过积分区域，穿入线ϕ1(y)\phi_{1}(y)为积分下限，穿出线ϕ2(x)

8.二重积分的计算视频讲解

\phi_{2}(x)为积分上限；第三步：计算重积分计算∫ϕ1(y)ϕ2(y)f(x,y)dx \int_{\phi_{1}(y)}^{\phi_{2}(y)} f(x, y) d x ，会得到一个关于。

9.二重积分计算举例

yy的多项式h(y)h(y)，再计算∫abh(y)dy\int_{a}^{b} h(y) d y得出最后结果二、如何确定积分限要计算区域DD上的二重积分∬Df(x,y)dσ\iint\limits_{D}^{}f(x, y) d \sigma。

10.二重积分咋计算

，假设DD是由曲线x2+y2=1x^{2}+y^{2}=1和直线x+y=1x+y=1所围成的区域，当先对yy后对xx积分时，确定积分限的步骤如下：①画草图：画出积分区域的草图并观察边界曲线。

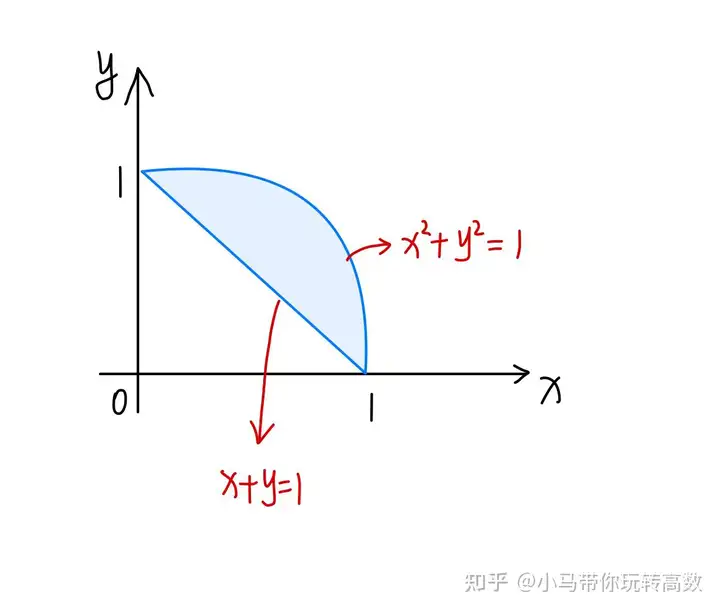
图1 画草图②若我们把积分区域看做“XX型”：确定xx的积分限这个相对容易，只要找出区域内xx的最小值x=0x=0和最大值x=1x=1，则xx的积分限为00到11③再确定yy的积分限，假设一条竖直线L

L沿着yy轴正方向纵穿区域DD，观察从围成积分区域穿过的穿入线和穿出线，穿入为积分下限，穿出则为积分上限这里yy的积分限要写成关于xx的函数形式，则积分下限（穿入线）为y=1−xy=1-x，积分上限（穿出线）为。

y=1−x2y=\sqrt{1-x^{2}}。

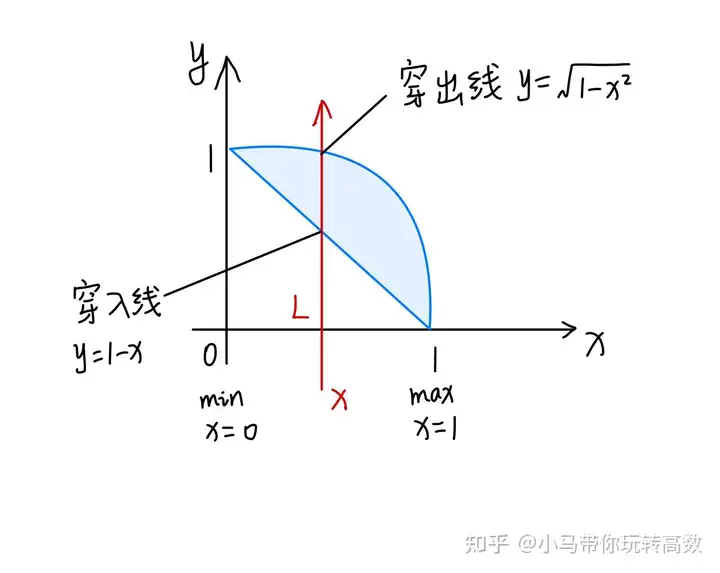
图2 X型区域的计算这样就确定了积分为： ∫01dx∫1−x1−x2f(x,y)dy\int_{0}^{1} dx\int_{1-x}^{\sqrt{1-x^{2}}} f(x,y)dy或∫01∫1−

x1−x2f(x,y)dydx\int_{0}^{1}\int_{1-x}^{\sqrt{1-x^{2}}} f(x,y)dydx此外，若看做“YY型”，也就是先对xx后对yy积分确定积分限的步骤也是一样的，只不过步骤2中的竖直线要变成沿着。

xx轴正方向横向穿过区域D的水平直线，xx的积分限写成关于y的函数形式，则积分变为：∫01dy∫1−y1−y2f(x,y)dx\int_{0}^{1}dy\int_{1-y}^{\sqrt{1-y^{2}}} f(x,y)dx

.

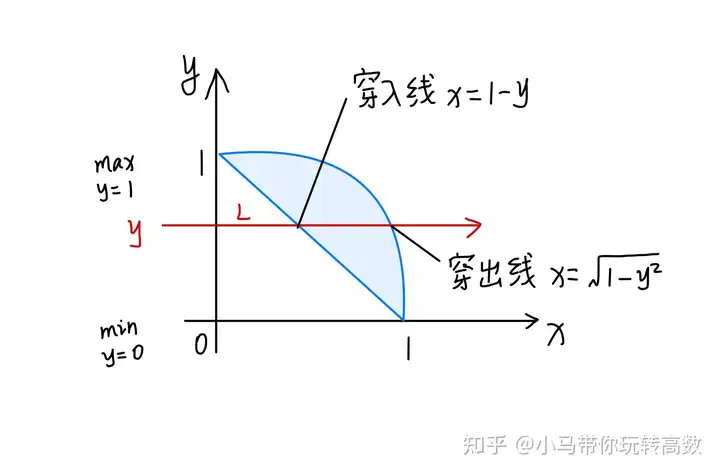
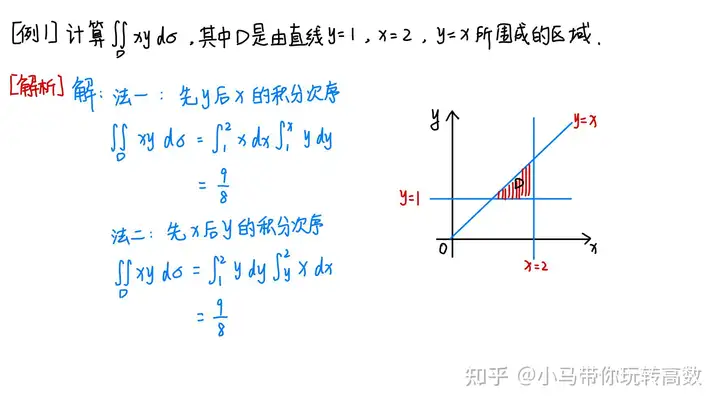
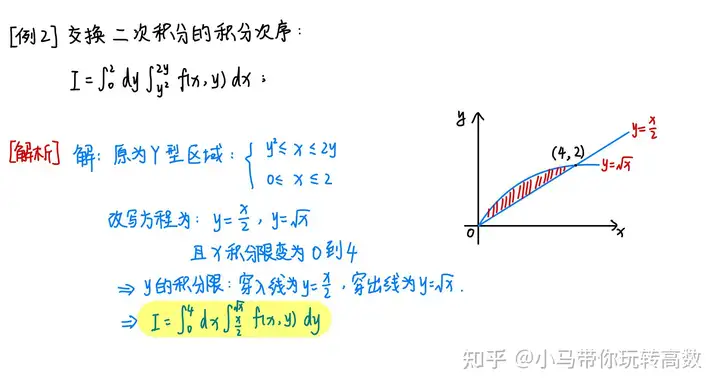
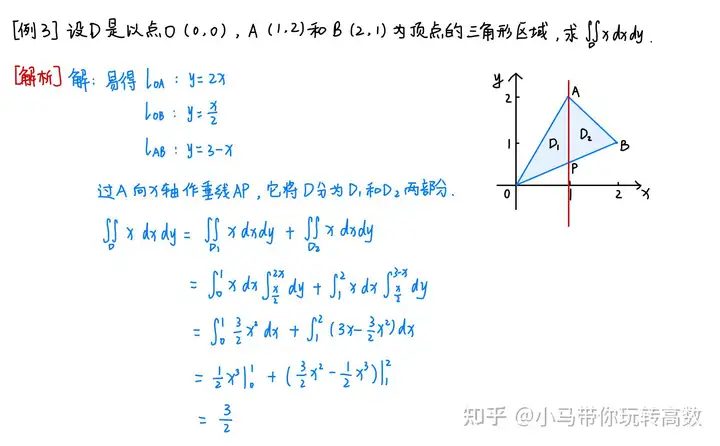
图3 Y型区域的计算三、例题精析