计算曲面体积（二重积分计算法）_曲面积分转化成二重积分

 

1.曲面积分转化为二重积分的公式

对于二重积分(double integral)的计算，一般通过二次定积分来实现对于黎曼积分(Riemann Integral)在区间上的积分值，在可积函数上可用来求被积函数的面积，因此对于二重积分可以求二元函数中空间上的曲面的体积，这里视作定积分的高维有向曲面的推广。

2.曲面积分如何化为二重积分

这里我们从几何意义上进行分析一.平面直角坐标系对于 ∬Df(x,y)dσ\iint_{D} f(x, y) d \sigma 假定一个二元函数 f(x,y)≥0f(x,y)\geq0 ，其积分区域D用不等式 。

3.求曲面体积二重积分

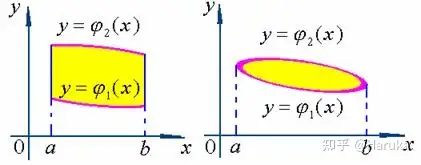
a⩽x⩽b,φ1(x)⩽y⩽φ2(x)a \leqslant x \leqslant b, \varphi_{1}(x) \leqslant y \leqslant \varphi_{2}(x) 表示，且

4.曲面积分化为二重积分

φ1(x),φ2(x)\varphi_{1}(x), \varphi_{2}(x) 在 [a,b]\left[ a,b\right] 连续有

5.曲面面积二重积分公式

因此依据其二重积分的几何意义，对于二重积分 ∬Df(x,y)dσ\iint_{D} f(x, y) d \sigma ，等于以 DD 为底，曲面 z=f(x,y)z=f(x,y) 为项的曲顶柱体的体积

6.曲面的二重积分

有

7.曲面二重积分几何意义

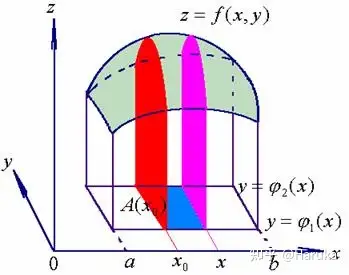
且在闭区间 [a,b]\left[ a,b \right] 中，取定一点 x0x_0 ,作平行于 yozyoz 面的平面 x=x0x=x_0 所截面积为曲面梯形，根据曲面梯形面积求法如图易得A(x)=∫

8.曲面积分变二重积分正负

ψ1,(x0)ψ2,(x0)f(x,y)dyA(x)=\int_{\psi_1,(x_0)}^{\psi_2,(x_0)} f(x, y) d y 此时利用嵌套定积分，已知截面面积求立体体积，有V=∫a

9.二重积分求曲面面积和体积什么区别

bA(x)dx=∫ab[∫ψ1(x)ψ2(x)f(x,y)dy]dxV=\int_{a}^{b} A(x) d x=\int_{a}^{b}\left[\int_{\psi_{1}(x)}^{\psi_{2}(x)} f(x, y) d y\right] dx

10.曲面积分化为二重积分怎么判断正负

可看作两次定积分的嵌套形式，此时为先对y，再对x的二次积分，二元函数看作一元函数的函数以此推广，对于任意二重积分存在∬Df(x,y)dσ=∫abdx∫ψ1,(x)ψ2,(x)f(x,y)dy\iint_{D} f(x, y) d \sigma=\int_{a}^{b} d x \int_{\psi_1,(x)}^{\psi_2,(x)} f(x, y) d y 。

根据其假定状况 f(x,y)≥0f(x,y)\geq0 ，但对于一般情况下的二重积分不受此条件限制，以上式子恒成立对于一般I=∫−11dx∫02(1−x2)dσ(D={(x,y)∣−1≤x⩽1,0≤y

≤2}\begin{array}{r} I=\int_{-1}^{1} d x \int_{0}^{2}\left(1-x^{2}\right) d \sigma(D=\{(x, y) \mid-1 \leq x \leqslant 1,0 \leq y \leq 2\} \end{array}

对于其二重积分dx微分形式有（仍以上述条件作为限制）∬Df(x,y)dσ=∫abdy∫ψ1,(y)ψ2,(y)f(x,y)dx\iint_{D} f(x, y) d \sigma=\int_{a}^{b} d y \int_{\psi_1,(y)}^{\psi_2,(y)} f(x, y) d x

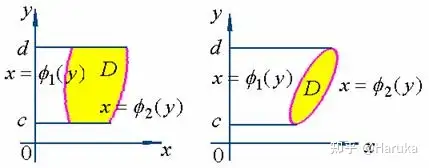
此时同理为先对x，再对y的二次积分。例题：计算二重积分 ∬Dxcos⁡(x+y)dσ\iint_{D} x \cos (x+y) d \sigma ，被积区域 DD 如图

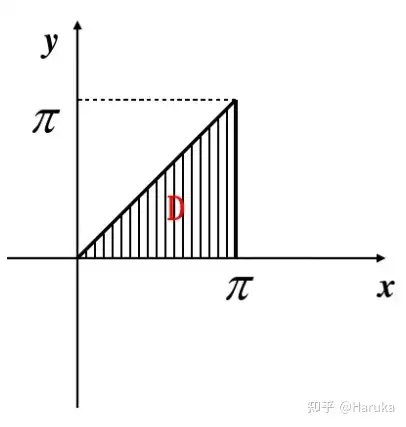
D区域所示有∬Dxcos⁡(x+y)dσ=∫0πdx∫0xxcos⁡(x+y)dy=∫0πxdx∫0xcos⁡(x+y)dy=∫0πxdx[sin⁡(x+y)]|0x\begin{aligned} & \iint_{D} x \cos (x+y) d \sigma \\ =& \int_{0}^{\pi} d x \int_{0}^{x} x \cos (x+y) d y \\ =& \int_{0}^{\pi} xdx \int_{0}^{x} \cos (x+y) d y \\ =& \int_{0}^{\pi} xdx [\sin (x+y)]|_{0} ^{x} \end{aligned}

此为平面直角坐标系，还有极坐标系下的推广二.极坐标系下的二重积分比起平面直角坐标系，极坐标系更好的表示其圆形扇形及环形对于 ∬Df(x,y)dσ \iint_{D} f(x, y) d \sigma

进行极坐标变换坐标曲线网对被积区域D进行分割， r=ar=a以O为圆心， rr 为半径的圆用 θ=b\theta=b ，O为起点的射线进行无穷分割设 Δσ\Delta\ \sigma 为 rr 到 r

+drr+dr 及 θ\theta 到 θ+dθ\theta+d\theta 小区域的面积，有Δσ=12(r+Δr)2Δθ−12r2Δθ\Delta \sigma=\frac{1}{2}(r+\Delta r)^{2} \Delta \theta-\frac{1}{2} r^{2} \Delta \theta

因此我们可以得到该二重积分的极坐标系形式∬Df(x,y)dσ=∬D′f(rcos⁡θ,rsin⁡θ)rdrdθ\iint_{D} f(x, y) d \sigma=\iint_{D^{\prime}} f(r \cos \theta, r \sin \theta) r d r d \theta

极坐标系下的二重积分以上式子由直角坐标系转换为极坐标系，以下介绍详细过程对于 Δσ=12(2r+Δr)ΔrΔθ=r+(r+Δr)2ΔrΔθ=r¯ΔrΔθ\begin{aligned} \Delta \sigma &=\frac{1}{2}(2 r+\Delta r) \Delta r \Delta \theta \\ &=\frac{r+(r+\Delta r)}{2} \Delta r \Delta \theta \\ &=\bar{r} \Delta r \Delta \theta \end{aligned}

r¯\bar{r} 为两圆弧半径平均值数学证明小区域求和的极限为零，因此下列步骤可以忽略在 Δσ\Delta \sigma 上取点 (r¯,θ¯)(\bar{r}, \bar{\theta}) ，设该点直角坐标为

(a,b)\left( a,b\right) ，根据极坐标及直角坐标转换公式有a=r¯cos⁡θ¯b=r¯sin⁡θ¯a=\bar{r} \cos \bar{\theta} \quad b=\bar{r} \sin \bar{\theta}

于是有limλ→0∑i=1nf(a,b)Δσ=limλ→0∑i=1nf(r¯cos⁡θ,r¯sin⁡θ)⋅r¯ΔrΔθ\begin{array}{l} \lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f(a, b) \Delta \sigma\\ =\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f(\bar{r} \cos \theta, \bar{r} \sin \theta) \cdot \bar{r} \Delta r \Delta \theta \end{array}

α⩽θ⩽β,φ1(θ)⩽r⩽φ2(θ)\alpha \leqslant \theta \leqslant \beta, \varphi_{1}(\theta) \leqslant r \leqslant \varphi_{2}(\theta)

动画演示参照Double Integrals2 – GeoGebra其中坐标系变换形式如下

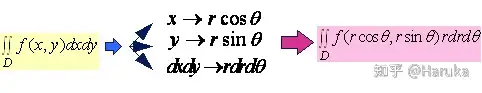
下面对此变换形式根据被积区域 DD 的取值，进行分情况讨论1. α⩽θ⩽β,φ1(θ)⩽r⩽φ2(θ)\alpha \leqslant \theta \leqslant \beta, \varphi_{1}(\theta) \leqslant r \leqslant \varphi_{2}(\theta)

，其中 φ1(θ)\varphi_1({\theta}) 和 φ2(θ)\varphi_2({\theta}) 在 [α,β]\left[ \alpha,\beta\right] 上连续

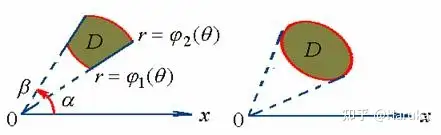
此时有∬Df(rcos⁡θ,rsin⁡θ)rdrdθ=∫αβdθ∫φ1(θ)φ2(θ)f(rcos⁡θ,rsin⁡θ)rdr\iint_{D} f(r \cos \theta, r \sin \theta) r d r d \theta=\int_{\alpha}^{\beta} d \theta \int_{\varphi_{1}(\theta)}^{\varphi_{2}(\theta)} f(r \cos \theta, r \sin \theta)rdr

2.第二种形式为第一种的变式（极点在积分区域的边界）

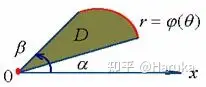
∬Df(rcos⁡θ,rsin⁡θ)rdrdθ=∫αβdθ∫0φ(θ)f(rcos⁡θ,rsin⁡θ)rdr\iint_{D} f(r \cos \theta, r \sin \theta) r d r d \theta=\int_{\alpha}^{\beta} d \theta \int_{0}^{\varphi(\theta)} f(r \cos \theta, r \sin \theta)rdr

3.第三种形式为第二种的变式(极点包围在积分区域 DD 的内部)

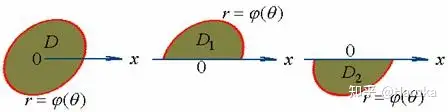
DD 可分割为 D1D_1 和 D2D_2 ，因此：，D：0≤θ≤2π，0≤r≤φ(θ)D：0\leq\theta\leq2\pi，0\leq r\leq\varphi(\theta) 有∬Df(rcos

⁡θ,rsin⁡θ)rdrdθ=∫02πdθ∫0φ(θ)f(rcos⁡θ,rsin⁡θ)rdr\iint_{D} f(r \cos \theta, r \sin \theta) r d r d \theta=\int_{0}^{2 \pi} d \theta \int_{0}^{\varphi(\theta)} f(r \cos \theta, r \sin \theta)rdr

综上讨论，将积分区域表示为 α⩽θ⩽β,φ1(θ)⩽r⩽φ2(θ)\alpha \leqslant \theta \leqslant \beta, \varphi_{1}(\theta) \leqslant r \leqslant \varphi_{2}(\theta)

形式方便进行极坐标上的运算例题：计算 ∬Df(x,y)dσ\iint_{D} f(x, y) d \sigma 在极坐标系下的二次积分 0)\right. ">D={(x,y)|x2+y2⩽a2}

(a>0)D=\left\{\left(x, y)|x^{2}+y^{2} \leqslant a^{2}\right\}(a>0)\right.

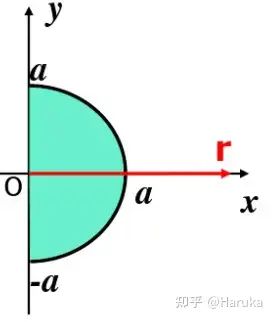
D的区域有∬Df(x,y)dσ=∬Df(rcos⁡θ,rsin⁡θ)rdr⁡dθ=∫−π2π2dθ∫0af(rcos⁡θ,rsin⁡θ)rdr\begin{aligned} \iint_{D} f(x, y) d \sigma&=\iint_{D} f(r \cos \theta, r \sin \theta) r \operatorname{dr} d \theta \\ &=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} d \theta \int_{0}^{a}f(r \cos \theta, r \sin \theta) rdr \end{aligned}

三.利用二重积分注意的问题在平面直角坐标系下，积分限的确定常常使用几何法

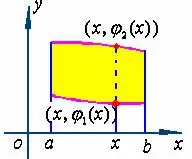
几何法假设积分区域 DD 如图所示，此时在闭区间 [a,b]\left[ a,b \right] 内任取一点x，过x轴平行于y轴做一条直线，与区域D存在两个交点，分别为 (x,φ1(x))\left( x,\varphi_1(x) \right)

和 (x,φ2(x))\left( x,\varphi_2(x) \right) ，此时将x看作常数后进行积分，但由于取于 [a,b]\left[ a,b \right] 所以此时上下限视作 b,ab,a

一般求三维空间内曲面体积的解法：1.作出该立体的简图,并确定它在 xoyxoy 面上的投影区域2.列出体积计算的表达式(二重积分法)3.配置积分限,化二重积分为二次积分并作定积分计算(几何法)极坐标系下的变换原则。

(1)、积分区域的边界曲线易于用极坐标方程表示(2)、被积函数表示式用极坐标变量表示较简单此时优先化作极坐标系下的二重积分后进行计算