【高数笔记】二重积分的计算（极坐标系）_二重积分极坐标怎么算详细过程

1.二重积分极坐标计算顺序

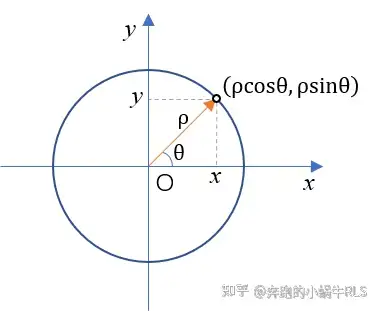
当二重积分的积分区域与圆有关时，使用直角坐标系来计算并不方便，但是我们可以把它转换为极坐标方程来处理我们先来看一下极坐标系和直角坐标系之间的转换关系：{x=ρcos⁡θy=ρsin⁡θ\begin{cases} x=\rho\cos \theta\\ y=\rho\sin \theta \end{cases}。

2.二重积分极坐标计算公式推导

.其实这就是很简单的三角函数关系。

3.二重积分极坐标使用条件

这样，我们只需要把被积函数 f(x,y)f(x,y) 替换为 f(ρcos⁡θ,ρsin⁡θ)f(\rho\cos \theta, \rho \sin \theta) 即可不过，替换过后函数的自变量也改变了，那么积分的面积元素也自然要跟着变一下。

4.二重积分极坐标法公式

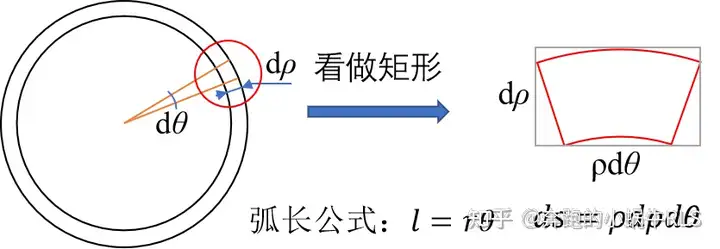
下面以圆为例讲解面积元素的计算方法仿照直角坐标系下面积元素的取法，我们在 (ρ,θ)(\rho,\theta) 处取一个圆心角为 dθd\theta ，宽度为 dρd\rho 的小扇环作为面积元素为了方便计算，我们不妨把这个小扇环看作一个矩形（当然也可以用大扇形面积-小扇形面积的方式进行计算，忽略掉高阶无穷小后的结果是一样的），那么它的长宽分别为 。

5.二重积分极坐标计算方法

ρ⋅dθ\rho\cdot d\theta （弧长）和 dρd\rho ，那么面积元素 dσ=ρdρdθd\sigma=\color{red}\rho d\rho d\theta .

6.二重积分极坐标怎么计算

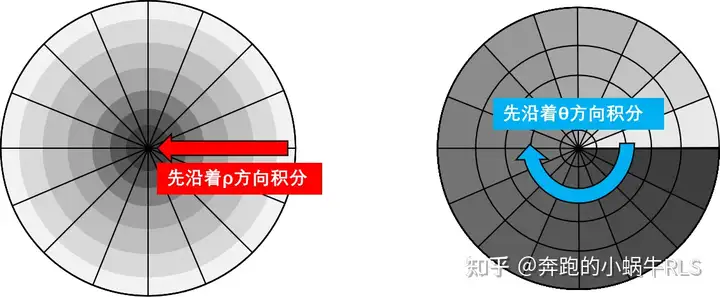
面积元素的计算现在我们有了被积函数的极坐标表达，也有了对应的面积元素，只需要想办法“遍历”所有面积元素并且与被积函数相乘并求和，也就是把二重积分转化为二次积分即可很显然，如果我们想要遍历整个被积区域，我们有两种选择，一种是“先θ后ρ”，另一种“是先ρ后θ”，如图所示。

7.二重积分极坐标怎么算详细过程

两种不同的积分顺序实际上，我们更常用的是第二种顺序，也就是先对θ积分剩下的内容我会用例题来说明例题 计算 ∬Ωxdσ\iint_\Omega xd\sigma ，其中Ω为方程 x2+y2=1x^2+y^2=1。

8.二重积分极坐标计算公式

所围成的区域解： 第一步：观察题目，发现被积区域与圆有关，考虑使用极坐标系进行积分第二步：用极坐标系表示被积函数、面积元素和被积区域原式= ∬Ωρcos⁡θ⋅ρdρdθ\iint_\Omega\rho\cos\theta\cdot\rho d\rho d\theta。

9.二重积分极坐标怎么算

.这里我们采用先对θ积分的顺序，所以在表示被积区域的时候应该先表示θ的范围，然后让ρ成为θ的函数，即：{0<θ<2π0<ρ<1\begin{cases} 0<\theta<2\pi\\ 0<\rho<1 \end{cases}

10.二重积分极坐标运算

.第三步：将二重积分化为二次积分注意：对某一个变量积分时，其它变量应该被看做常数原式= ∫01∫02πcos⁡θρ2dθdρ\int_0^1\int_0^{2\pi}\cos\theta \rho^2 d\theta d\rho。

.第四步：计算二次积分我们先把ρ看作常数，计算内层对θ的积分；然后计算外层对ρ的积分，这时候外层积分中已经不含有θ了很容易计算出结果为0.总结一下，用极坐标计算二重积分主要分为一下几个步骤：①将题中表达式（被积函数和面积元素）改写为极坐标形式；。

②用极坐标系表示出被积区域，注意顺序，后面表达的变量是前面的变量的函数；③将二重积分改为二次积分；④计算二次积分，注意顺序要与被积区域的表达顺序一致。