重积分 第二节 二重积分的计算法_二重积分的计算规则

 

2. 二重积分的计算法

目前所能接触到的方法是： 将二重积分化为两次单积分将二重积分化为两次单积分_\underline{将二重积分化为两次单积分}

​ 接下来介绍：① 直角坐标系 ② 极坐标 ③ 二重积分的换元法（至于二重积分的换元法，仅作简单介绍）

2.1 利用直角坐标计算二重积分

​ 本质思想是通过画图来判断是先对 xx 还是先对 yy 积分。

（先对哪一个积分不绝对，需要具体问题具体分析，但仍需考虑图形，这里不过多解释为什么，仅给出相关题型的做法）

下面的介绍中，默认 f(x,y)≥0f(x,y) ≥ 0

① 有如下闭区域 DD ：

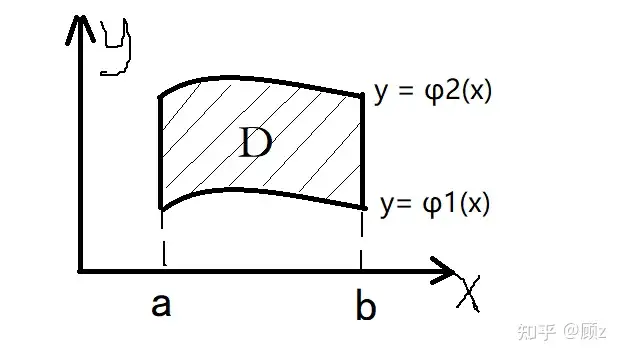
∬Df(x,y)dσ=∫abdx∫ϕ1(x)ϕ2(x)f(x,y)dy\iint_D f(x,y) \ d\sigma = \int_a^{b}dx\int_{\phi_1(x)}^{\phi_2(x)}f(x,y)\ dy （先对 yy 后对 xx ）

②

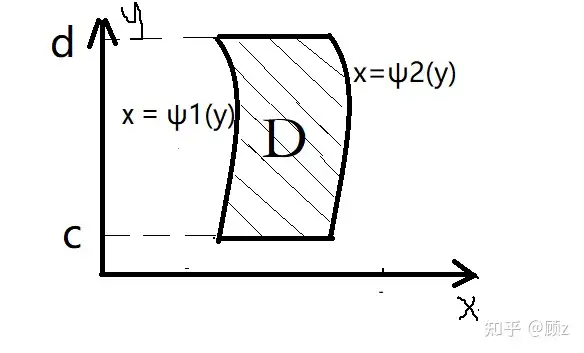
∬Df(x,y)dσ=∫cddy∫ψ1(y)ψ2(y)f(x,y)dx\iint_D f(x,y) \ d \sigma = \int_c^d dy \int_{\psi_1(y)}^{\psi2(y)}f(x,y) \ d x （先对 xx 后对 yy ）

（注：这里未考虑在立体空间中的形状，但只研究物体在 xOyxOy 面上的投影即可解决问题）

​ 我们称①、②中的区域分别为 XX 型区域、 YY 型区域。（按先对 、x、yx、y 中的哪个积分来命名）

​ 若闭区域 DD 既是 XX 型区域，又是 YY 型区域，则选择哪一种都可以（尽量找简单的）

不管先对还是进行积分，要找准积分限不管先对x还是y进行积分，要找准积分限\color{red}{不管先对x还是y进行积分，要找准积分限}

​ “每个人都有每个人的理解方式，这里我有些解释不出来，大家自行领会吧”

注： 在解题时，注意使用 可加性"可加性"\color{red}{"可加性"} ，区间可以分为 XX 型、 YY 型，既是 XX 型又是 YY 型的，此时我们对其分别求二重积分即可。

这里给出一个例子来让大家认识到选择正确的积分次序的重要性：

​ 计算 ∬Dy1+x2−y2dσ\iint_Dy \sqrt{1+x^2-y^2}\ d \sigma ，其中区域 DD 是由 、、y=x、x=−1、y=1y=x、x=-1、y=1 围成的闭区域。

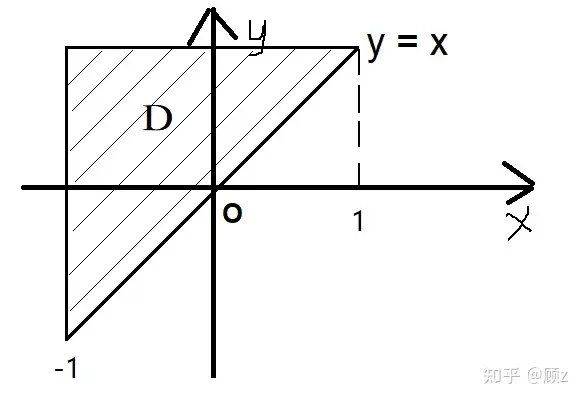
​ 显然 DD 既是 XX 型，又是 YY 型积分区域，现在我们用两种方法来看一下：

​ ① 先对 yy 后对 xx ： ∫−11dx∫x1y1+x2−y2dσ\int_{-1}^{1}dx \int_{x}^{1}y\sqrt{1+x^2-y^2}\ d \sigma

（偶函数，想想为什么这里是）=−13∫−11[(1+x2−y2)32|x1]dx=−13∫−11(|x|3−1)dx_（偶函数，想想为什么这里是|x|3）=−23∫01(x3−1)dx=−23(x44−x)|01=−23⋅(14−1)=12= -\frac{1}{3}\int_{-1}^{1}\Bigg[(1+x^2-y^2)^{\frac{3}{2}}\Big\rvert_{x}^{1}\Bigg]\ d x \\=-\frac{1}{3}\underline{\int_{-1}^{1}(|x|^3-1)\ dx} （偶函数，想想为什么这里是|x|^3）\\ = -\frac{2}{3}\int_{0}^{1}(x^3-1)dx\\ = -\frac{2}{3}(\frac{x^4}{4}-x)\Big\rvert_{0}^{1} \\\ =-\frac{2}{3}\cdot(\frac{1}{4}-1)=\frac{1}{2} ​

②先对 xx 后对 yy ： ∫−11dy∫y1y1+x2−y2dx\int_{-1}^{1}dy\int_{y}^{1}y\sqrt{1+x^2-y^2}dx =∫−11[xy(1+x2−y2)12|1y−∫1yxd[y(1+x2−y2)12]]=∫−11[y2−y2−y2−∫1yx2y1+x2−y2dx]dy= \int_{-1}^{1}\Bigg[xy(1+x^2-y^2)^{\frac{1}{2}}\Big\vert_{1}^{y} -\int_{1}^{y}x\ d\Big[y(1+x^2-y^2)^{\frac{1}{2}}\Big]\Bigg] \\ = \int_{-1}^{1}\Bigg[y^2-y\sqrt{2-y^2}-\int_{1}^{y}\frac{x^2y}{\sqrt{1+x^2-y^2}}\ dx \Bigg]dy ​

此时还需求 ∫1yx2y1+x2−y2dx\int_{1}^{y}\frac{x^2y}{\sqrt{1+x^2-y^2}}\ dx ，难免比较麻烦。后面的步骤这里就不写了（或许这样不对，但是想必大家已经意识到了麻烦。）

​ （这里分部积分或许不是最好的做法，但主要还是为了让大家知到积分次序的重要性）

2.2 利用极坐标计算二重积分

​ 核心思想：将 、x、yx、y 写为 ρ⋅cosθ,ρ⋅sinθ\rho \cdot cos\theta,\rho \cdot sin\theta ，即极坐标形式求解。

​ 适用题型：不规则的/规则的扇形、圆形...

​ 式子： ∬Df(x,y)dxdy=∬Df(ρ⋅cosθ,ρ⋅sinθ)ρ⋅dρdθ_\iint_D f(x,y)\ dx dy=\iint_D f(\rho \cdot cos\theta,\rho \cdot sin\theta)\underline{\rho \cdot d \rho d \theta} （积分次序一般先对 ρ\rho 后对 θ\theta ）

这里扯点题外话，为什么 dxdy→ρ⋅dρdθdxdy\rightarrow \rho \cdot d\rho d\theta ？（这里不涉及坐标变换的雅可比行列式，我也不太会...）

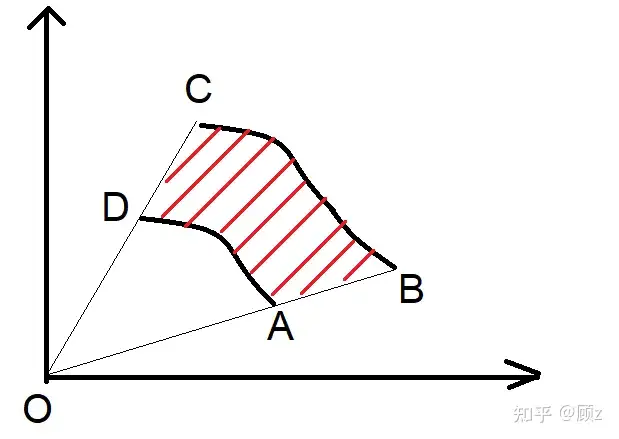
​ 在二重积分中：积分元为 ABCD_\underline{ABCD}

​ 且 OA=ρ,AB=dρ,∠AOD=dθOA=\rho,AB=d\rho,\angle AOD =d \theta

​ 弧 AD=ρ⋅dθAD=\rho \cdot d\theta ，当 dθd\theta 足够小的时候，我们将 ABCDABCD 近似为一个矩阵就有： dS=ρ⋅dρdθd S=\rho \cdot d\rho d\theta

​ (\Big( 因为二重积分的积分元(也就是之前分割得到的小矩形)是极其小的面积，因此用面积进行考虑。而这也就是为什么 ρ⋅dρθ\rho\cdot d \rho \theta 被称为极坐标系中的面积元素 )\Big)

一些课本上的扩展知识这里就不给太多了，要不然用课本干什么-.-。

这里给一下 ∬De−x2−y2dxdy\iint_De^{-x^2-y^2}dxdy 的计算过程，其中 DD 为圆心在原点，半径为 aa 的圆周所围成的闭区域。 遇到，一般考虑化为极坐标遇到x2+y2，一般考虑化为极坐标\color{red}{遇到x^2+y^2，一般考虑化为极坐标}

​ 则 原式原式=∬De−ρ2ρ⋅dρdθ=∫02πdθ∫0ae−ρ2ρ⋅dρ=2π⋅(−12e−ρ2)|0a=−π(e−a2−1)=π(1−e−a2) 原式=\iint_D e^{-\rho^2}\rho \cdot d\rho d\theta=\int_0^{2\pi}d\theta\int_0^{a}e^{-\rho^2}\rho\cdot d\rho \\=2\pi\cdot (-\frac{1}{2}e^{-\rho^2})\Big|_{0}^{a} \\=-\pi(e^{-a^2}-1)=\pi(1-e^{-a^2}) ​ 这里涉及到了一个小知识点：由于对 ρ\rho 积分未涉及到 θ\theta ，就可以直接计算 ∫02πdθ=2π\int_{0}^{2\pi}d\theta =2\pi

​ （后面会很常用/大家的老师应该有讲）

​ 依此方法，就可求出工程上常用的反常函数 ∫0+∞e−x2dx=π2\int_{0}^{+\infty}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}

（这里就不写出过程了，想要了解的可以自行查阅一下课本）

*2.3 二重积分的换元法

​ 这部分就不给大家介绍了，（我也不太会），貌似这里可以与线性代数相关联而让一些地方变得易懂一些？

2.4 例题

​ 直接结束显得太草率了，再给出一个题吧：[题源：《高等数学下》同济版p158 14.(3)]

计算 ∬Darctanyxdσ\iint_D arctan \frac{y}{x}\ d\sigma ，其中 DD 是由圆周 x2+y2=4,x2+y2=1x^2+y^2=4,x^2+y^2=1 及直线 y=0,y=xy=0,y=x 围成的在第一象限的闭区域

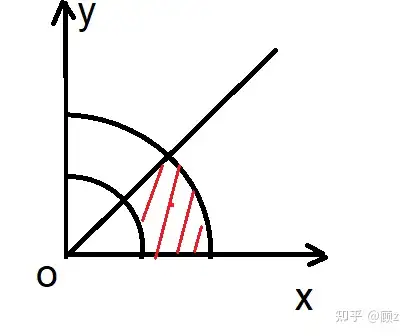
积分区域为扇形状，考虑使用极坐标： x=ρ⋅cosθ,y=ρ⋅sinθ,yx=tanθx=\rho \cdot cos\theta,y=\rho \cdot sin\theta,\frac{y}{x}=tan\theta

原式原式=∫0π4dθ∫12arctantanθ⋅ρdρ=∫0π4θ⋅dθ∫12ρ⋅dρ=12(θ2)|0π4⋅12(ρ2)|12=12×π216×12×(4−1)=3π264原式=\int_{0}^{\frac{\pi}{4}}d\theta\int_{1}^{2}arctan tan\theta \cdot \rho d\rho \\ =\int_{0}^{\frac{\pi}{4}}\theta \cdot d\theta \int_{1}^{2}\rho \cdot d\rho \\ =\frac{1}{2}(\theta^2)\Big|_{0}^{\frac{\pi}{4}} \cdot \frac{1}{2}(\rho^2)\Big|_{1}^{2} \\ = \frac{1}{2}\times\frac{\pi^2}{16}\times\frac{1}{2}\times(4-1) = \frac{3\pi^2}{64}

​ 不管是二重积分还是后面的三重积分，甚至多重积分，都对积分的计算有一定的要求，还希望大家能够打好基础。