欧拉公式-欧拉公式的推导

三角形的外心与内心之间的距离d与其外接圆和内切圆的半径分别为R、r，那么

1R+d+1R−d=1r\frac{1}{R+d}+\frac{1}{R-d}=\frac{1}{r}\\

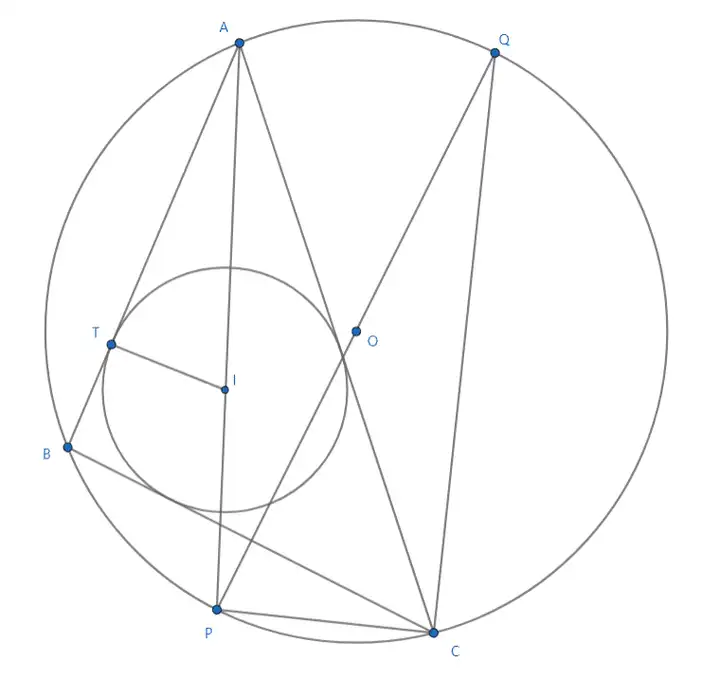
证明：如图，三角形ABC的外心和内心分别为O和I,连AI的延长线交于外接圆于P，连接PO并延长交于外接圆于Q，连接QC、PC；假设内切圆与AB的切点为T，那么

IT=rPQ=2R△QPC∼△AIT∴QP⋅IT=AI⋅PC∴AI⋅PC=2R⋅rIT=r\\PQ=2R\\\triangle{QPC}\sim\triangle{AIT}\\\therefore QP\cdot IT=AI\cdot PC\\\therefore AI\cdot PC=2R\cdot r\\

由相交弦定理可知

AI⋅IP=(R−d)(R+d)AI\cdot IP=(R-d)(R+d)\\

要注意到I是内心，那么

∠PCB=∠PAB=12∠A∠BCI=∠ACI=12∠C∠PCI=∠PCB+∠BCI=12∠A+12∠C∠PIC=∠PAC+∠ACI=12∠A+12∠C∴PI=PC∴AI⋅PC=AI⋅IP=(R−d)(R+d)\begin{aligned} \angle PCB&=\angle PAB=\frac{1}{2}\angle A\\ \angle BCI&=\angle ACI=\frac{1}{2}\angle C\\ \angle PCI&=\angle PCB+\angle BCI=\frac{1}{2}\angle A+\frac{1}{2}\angle C\\ \angle PIC&=\angle PAC+\angle ACI=\frac{1}{2}\angle A+\frac{1}{2}\angle C\\ \therefore\quad PI&=PC\\ \therefore\quad AI\cdot PC&=AI\cdot IP=(R-d)(R+d) \end{aligned}\\

所以

2R⋅r=(R−d)(R+d)2R\cdot r=(R-d)(R+d)\\

即

1R+d+1R−d=1r\frac{1}{R+d}+\frac{1}{R-d}=\frac{1}{r}\\

该命题的证明用到了多个知识点：相交弦定理，三角形的内心，相似三角形，相等的圆弧对应相等的圆周角。这个公式也是很漂亮的，不要说你没看出来(不懂得鉴赏美~没审美~)！想想看，给定一个三角形，它的外心和内心就给定了，而两心间的距离也是命中注定了啊。两颗“心”注定有距离。这个公式被命名为欧拉公式，当然了被称为欧拉公式的式子可不止这一个，比如大名鼎鼎的全宇宙最美数学公式：eπi+1=0e^{\pi i}+1=0。从名称上看，该公式应该是大师欧拉先发现的了，这么漂亮的公式发现的有点晚了。