【复数的浪漫】上帝的公式——欧拉公式-欧拉的上帝公式是怎么证明的

 

很多科普文章介绍欧拉公式总是从 exp⁡z\exp z 、 sin⁡z\sin z 、 cos⁡z\cos z 这三个函数的泰勒展开入手，今天我们不这样做。我们要从几何角度入手，看到欧拉公式是多么自然直观。但在此之前，我们要铺垫一些复变函数的内容，请不要感到厌烦！

点赞，能有效激发劳动者的积极性，所以，请点个赞吧！

复变函数的可视化

早在中学阶段，我们就学习了实变函数，它的定义域和值域都是 R\mathbb{R} 的子集；现在，让我们探讨复变函数，它的定义域和值域都是 C\mathbb{C} 的子集

为了展现实变函数的性质，我们可以在 xx - yy 平面内作出函数的图像。但是，由于复数是二维的，作出复变函数的图像需要四维的空间，这超乎我们粗浅的认知。所以，我们不妨换一种方式看待复变函数。

我们考虑函数 f(z)=z2f(z)=z^2

代入 z=1z=1 ，得到 f(z)=1f(z)=1

代入 z=2z=2 ，得到 f(z)=4f(z)=4

代入 z=−1z=-1 ，得到 f(z)=1f(z)=1

代入 z=iz=i ，得到 f(z)=−1f(z)=-1

......

实变函数把数轴上的一个点映射到数轴上另一个点，同样地，复变函数也把复平面上的一个点映射到复平面上的另一个点。我们把复平面上所有点易位的过程以动画呈现，这就是复变函数的可视化。

根据复数乘法的几何意义，我们知道， z2z^2 就是将 zz 的辐角变为原来的 22 倍，模长变为原来的平方。

这一点在动画里得到了很好的呈现：模长为 11 的复数都在绕单位圆旋转，这是因为 12=11^2=1 ，其模长不会变；而实轴上的点始终在实轴上，只发生伸缩，这是因为其辐角为 00 ， 00 的 22 倍依然为 00 ；而复平面上其它的点，则是一边旋转，一边伸缩。

复变函数的导数

在 R\mathbb{R} 上，因为实数是一维量，xx 的变化只能沿着 xx 轴，只有一个方向。于是， Δx\Delta x 只具有一个参量：长度

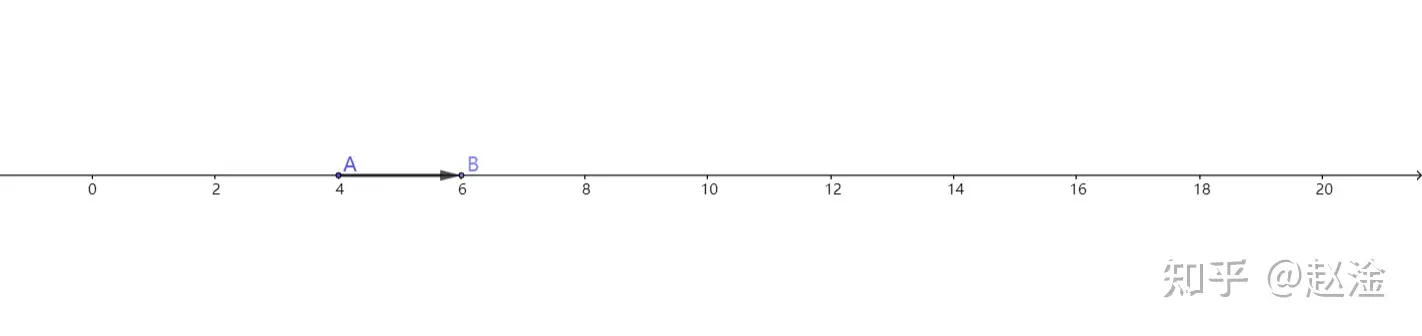
但是，在 C\mathbb{C} 上，事情就不一样了。因为复数是二维量， zz 可以朝着四周任何一个方向变化。这时，只用一个参量描述 zz 的变化就显得欠缺了，我们还要引入辐角这个参量。

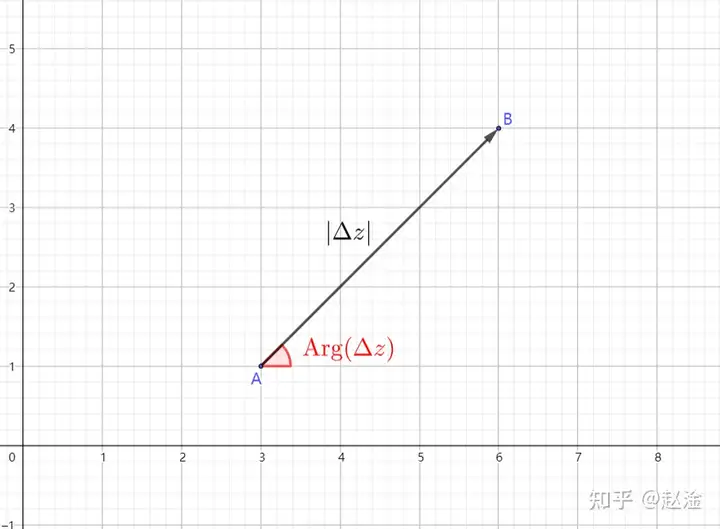
当自变量 zz 发生变化 Δz\Delta z 时，因变量 ww 也会对应产生变化 Δw\Delta w ，我们让 μ=ΔwΔz\mu=\frac{\Delta w}{\Delta z} ，这个式子代表什么意义呢？

根据复数除法的几何意义，我们很容易发现：

|μ|=|Δw||Δz|Arg(μ)=Arg(Δw)−Arg(Δz)\begin{eqnarray} |\mu|&=&\frac{|\Delta w|}{|\Delta z|}\\ \text{Arg}(\mu)&=&\text{Arg}(\Delta w)-\text{Arg}(\Delta z) \end{eqnarray}\\

这说明， |μ||\mu| 代表的是 |Δw||\Delta w| 与 |Δz| |\Delta z| 的“兑换率”：当 zz 的模长增加或减少 dd 时， ww 的模长将对应增加或减少 |μ|d|\mu|d ； Arg(μ)\text{Arg}(\mu) 则代表着 Δw\Delta w 与 Δz\Delta z 的夹角，如下图所示。

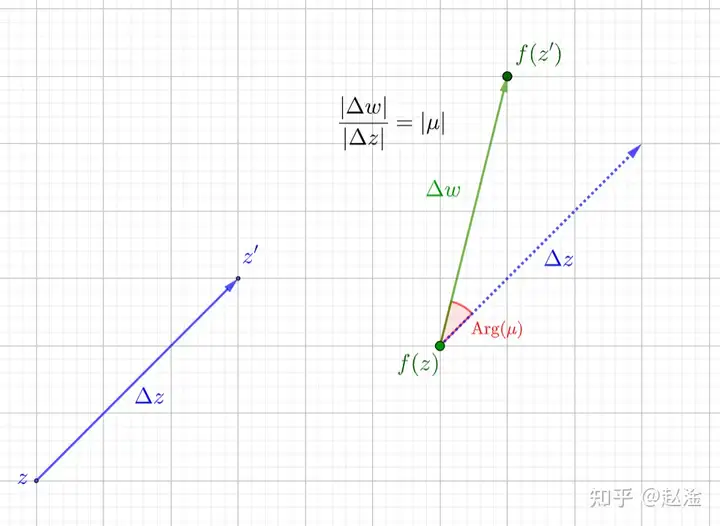
以 z0z_0 为起点，朝着任意方向取一个极小的变化量 Δz\Delta z 时，如果 ΔwΔz\frac{\Delta w}{\Delta z} 存在且恒为 AA ，就称 f(z)f(z) 在 z0z_0 处可导且导数为 AA

可导意味着：以 z0z_0 为起点，朝着任意方向取一个极小的变化量 dz\mathrm{d} z 时， dw\mathrm{d}w 的长度恒为 dz\mathrm{d}z 长度的 |A||A| 倍， 而且 dw\mathrm{d}w 与 dz\mathrm{d}z 的夹角恒为 Arg(A)\text{Arg}(A) ，如下面的视频所示

设 f(x+yi)=u(x,y)+v(x,y)if(x+yi)=u(x,y)+v(x,y)i，当我们选取两个比较特殊的 dz\text{d} z 时，可以得到复变函数可导的条件

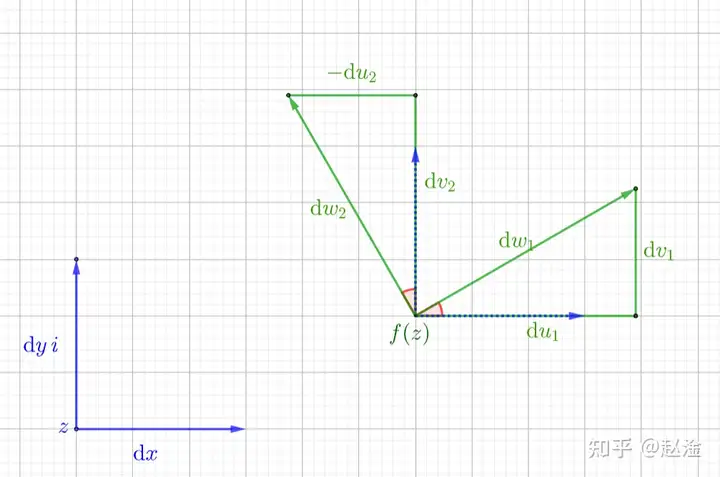
首先，我们取 dz\text{d}z 为水平向右前进 dx\mathrm{d}x ，对应产生 dw1\text{d}w_1 ，容易知道，其水平和竖直分量分别为：

du1=∂u∂xdx,dv1=∂v∂xdx\text{d}u_1=\frac{\partial u}{\partial x}\text{d}x\,,\text{d}v_1=\frac{\partial v}{\partial x}\text{d}x\\

然后，我们取 dz\text{d}z 为竖直向上前进 dy\mathrm{d}y ，对应产生 dw2\text{d}w_2 ，容易知道，其水平和竖直分量分别为：

du2=∂u∂ydy,dv2=∂v∂ydy\text{d}u_2=\frac{\partial u}{\partial y}\text{d}y\,,\text{d}v_2=\frac{\partial v}{\partial y}\text{d}y\\

由可导的几何意义，图中两个红色的角相等，我们再让 dx=dy\text{d}x=\text{d}y ，则两个绿色三角形全等，有：

dv1=−du2du1=−dv2\mathrm{d}v_1=-\mathrm{d}u_2\\ \mathrm{d}u_1=-\mathrm{d}v_2\\

即： ∂v∂x=−∂u∂y∂u∂x=∂v∂y\begin{eqnarray} \frac{\partial v}{\partial x}&=&-\frac{\partial u}{\partial y}\\ \frac{\partial u}{\partial x}&=&\frac{\partial v}{\partial y} \end{eqnarray}\\ \begin{eqnarray} \end{eqnarray}

此即柯西-黎曼方程

指数函数的构造 欧拉公式

指数函数是我们的老朋友了，现在，我们希望把它拓展到复数域上。指数函数最令我们着迷的性质是什么？求导等于本身！所以，我们希望在 C\mathbb{C} 上找到这样一个函数，它的导数等于本身，我们记这个函数为 exp⁡z\exp z ，则：

d(exp⁡z)dz=exp⁡z\frac{\mathrm{d}(\exp z)}{\text{d}z}=\exp z\\ 根据导数的几何意义，d(exp⁡z)\mathrm{d}(\exp z) 与 dz\text{d}z 的夹角等于 exp⁡z\exp z 的辐角，这一点颇重要。

我们取 dz\text{d}z 为水平向右前进，则 d(exp⁡z)\mathrm{d}(\exp z) 与 dz\text{d}z 的夹角就是 d(exp⁡z)\mathrm{d}(\exp z) 的辐角，它等于 exp⁡z\exp z 的辐角。从图像上看， exp⁡z\exp z 只发生了伸缩，且 |d(exp⁡z)||dz|=|exp⁡z|\displaystyle{\frac{|\mathrm{d}(\exp z)|}{|\text{d}z|}=|\exp z|}

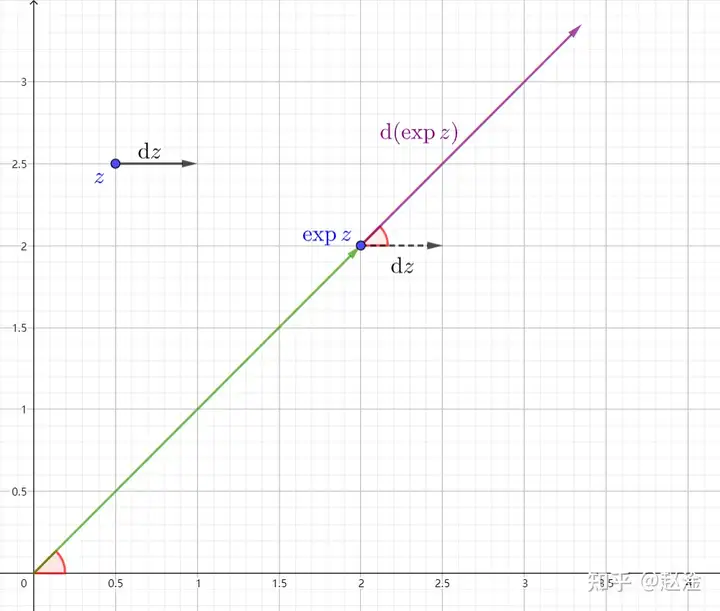
我们取 dz\mathrm{d}z 为竖直向上前进，如图所示， d(exp⁡z)\mathrm{d}(\exp z) 将垂直于 exp⁡z\exp z ，而 d(exp⁡z)\mathrm{d}(\exp z) 很小，可以认为 exp⁡z\exp z 逆时针旋转了一个小角度 θ\theta 且 θ∼tan⁡θ=|d(exp⁡z)||exp⁡z|=|dz|\displaystyle{\theta\sim \tan\theta=\frac{|\text{d}(\exp z)|}{|\exp z|}=|\text{d}z|}

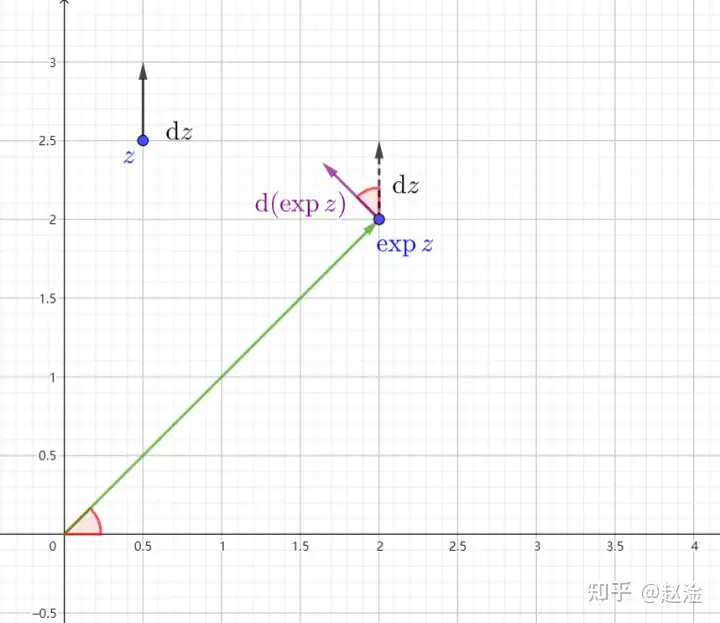
我们总结一下：

当 zz 仅有实部发生变化时， exp⁡z\exp z 的辐角不变，发生伸缩当 zz 仅有虚部发生变化时， exp⁡z\exp z 的模长不变，发生旋转

下面，让我们推证 exp⁡z\exp z 的表达式

首先，我们知道 z=x∈Rz=x\in \mathbb{R} 时， exp⁡z=ex\exp z=e^x ，其模长为 exe^x ，辐角为 00

现在我们让 zz 的虚部变为 yy ，即 z=x+yiz=x+yi ，在这个过程中， exp⁡z\exp z 的模长不变，仍为 exe^x ； exp⁡z\exp z 的辐角很容易积出来：

θ=∫0y|dz|=∫0ydy=y\theta=\int_0^y |\text{d}z|=\int_0^y \text{d}y=y\\

所以， exp⁡(x+yi)\exp(x+yi) 应该是以 exe^x 为模长， yy 为辐角的复数，即：

exp⁡(x+yi)=ex(cos⁡y+isin⁡y)\boxed{\exp(x+yi)=e^x(\cos y+i\sin y)}\\

如果我们令 x=0,y=πx=0,y=\pi ，我们将得到 exp⁡(πi)=−1\exp(\pi i)=-1 ，或它更广为人知的形式：

eπi+1=0\boxed{e^{\pi i}+1=0}\\

这就是欧拉公式（Eulers Formula）——上帝的公式