平面图的欧拉公式及其推论-平面图中的欧拉公式

 

在图论中，一个图（graph）由它的顶点（vertex）和边（edge）构成。对于一个画在平面或球面上的图，如果除在顶点外，任意两边不交叉，此图叫做平面图（planar graph）。平面中被图分成的连通区域叫作面（face）。平面图的欧拉公式（不是经典的 eiπ+1=0e^{i\pi}+1=0 ）对平面图的顶点数、边数和面数给出了一个简单的关系，它第一次出现于欧拉（Euler）给哥德巴赫（Goldbach）的信件中。

1 欧拉公式

我们这里介绍的欧拉公式的证明用到了对偶图（dual graph）的概念。每个图 MM 都对应一个对偶图 GG ，其中 MM 的每一个区域对应 GG 中的一个顶点（vertex）， MM 中共边的两个区域对应连接 GG 中两顶点的边（edge）。

对偶图

定理（欧拉公式）令 G=(V,E)G=(V,E) 为一个连通的平面图，其中 VV 是顶点的集合， EE 是边的集合，并令 RR 为面的集合. 那么， |V|−|E|+|R|=2|V|-|E|+|R|=2 .

证明 令 T⊂ET\subset E 为 GG 的生成树（spanning tree）的边的集合，生成树是最小的连接 GG 的每个顶点的子图. 由于其最小性，生成树不含圈（cycle）.

生成树

考虑 GG 的对偶图 G∗=(V∗,E∗)G^*=(V^*,E^*) ，以及对应 GG 中边集 E∖TE\setminus T 的 G∗G^* 中边集 T∗⊂E∗T^*\subset E^* . 注意 T∗T^* 中的边和 TT 中的边不相交. 由于 TT 不含圈， T∗T^* 使对应 GG 中所有面的顶点连通. 另外 T∗T^* 也不含圈，否则 TT 不是连通的. 这样，我们就得到， T∗T^* 是 G∗G^* 的一个生成树，也被称作 GG 的一个对偶生成树（dual spanning tree）.

生成树和对偶生成树

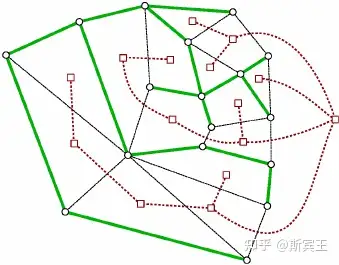
每个树的顶点数都比边数大 11 . 若选择一个顶点作为根，并把每条边对应到从根离开方向所指向的顶点，我们就构造了一个生成树中除根之外所有顶点和所有边的双射（bijection）.

将此结论应用到 GG 和 G∗G^* ，我们有 |V|=|ET|+1|V|=|E_T|+1 和 |R|=|ET∗|+1|R|=|E_{T^*}|+1 . 由于 |E|=|ET|+|ET∗||E|=|E_T|+|E_{T^*}| ， |V|+|R|=|E|+2|V|+|R|=|E|+2 .

欧拉公式有许多有趣且重要的推论，其中最直接的一个是表明完全图（complete graph） K5K_5 和完全二分图（complete bipartite graph） K3,3K_{3,3} 不是平面图。这里，完全图是指每对不同顶点恰有一条边相连的图，二分图是指顶点集可分割为两个互不相交的子集的图，并且图中每条边的两个顶点都分别属于这两个子集，两个子集内的顶点不相邻，而完全二分图是指每对不同的分别属于两个子集顶点恰有一条边相连的二分图。在此之前，我们先介绍度数（degree）的概念。以一个顶点为端点的边的个数叫作此顶点的度数，其中自环（loop）算两次。

K5和K3,3

命题 完全图 K5K_5 和完全二分图 K3,3K_{3,3} 不是平面图.

证明 令 GG 为一个图，并令 nn 为图 GG 的顶点数， ee 为图 GG 的边个数，且 nin_i 为度数为 ii 的顶点数. 若用度数来计算顶点数， n=n0+n1+n2+⋯n=n_0+n_1+n_2+\cdots ，而若用度数来计算边数，由于每条边对应两个顶点， 2e=n1+2n2+3n3+⋯2e=n_1+2n_2+3n_3+\cdots . 用顶点的总度数除以顶点个数，我们得到，平均度数 d¯=2en\overline{d}=\frac{2e}{n} .

顶点的度数

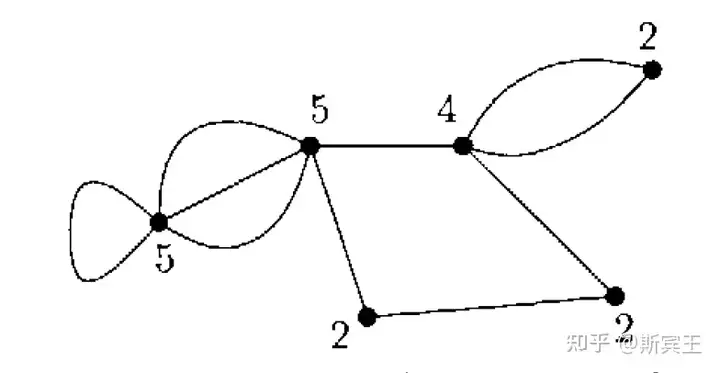
令 ff 为图 GG 的面数，且 fkf_k 为有 kk 条边的面数. 若计算面数， f=f1+f2+f3+⋯f=f_1+f_2+f_3+\cdots ，而若将边视作面的边界来计算边数， 2e=f1+2f2+3f3+⋯2e=f_1+2f_2+3f_3+\cdots . 这样，我们得到，面的平均边数是 f¯=2ef\overline{f}=\frac{2e}{f} .

面的边数

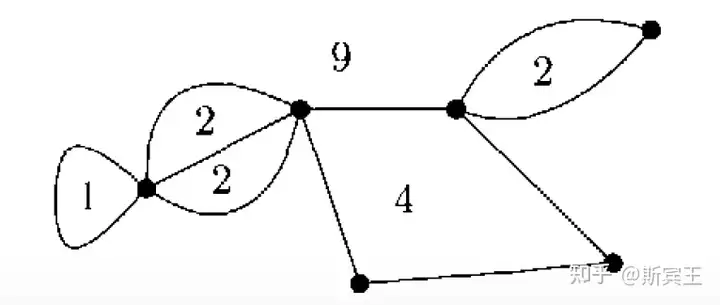
假设 K5K_5 存在平面图画法，那么 n=5n=5 ， e=(52)=10e=\binom{5}{2}=10 ，故 f=e−n+2=7f=e-n+2=7 ，所以平均面数为 f¯=2ef=207<3\overline{f}=\frac{2e}{f}=\frac{20}{7}<3 . 这样，必须有一个面的边数小于等于 22 ，而这对于完全图是不可能的，因为每对不同顶点都只有一条边相连.

类似地，对于 K3,3K_{3,3} ， n=6n=6 ， e=9e=9 ，故 f=e−n+2=5f=e-n+2=5 ，所以平均面数为 f¯=2ef=185<4\overline{f}=\frac{2e}{f}=\frac{18}{5}<4 . 这是不可能的，因为完全二分图的每个圈（cycle）的边数至少是 44 .

有一个交点的K5有一个交点的K3,3

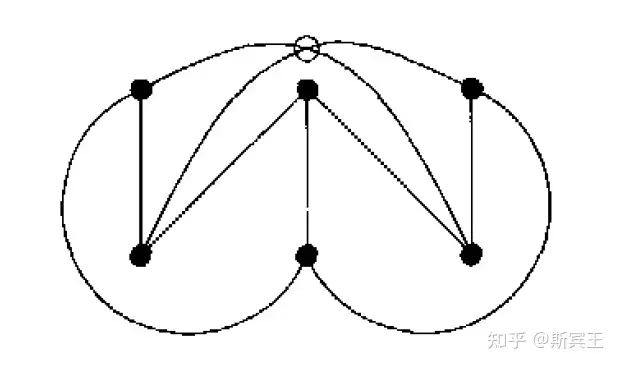
2 局部推论

根据双计数恒等式（double counting identity），我们可以得到欧拉公式的局部推论。

命题 令 GG 是顶点数 2">n>2n>2 的简单平面图（关联任一对顶点的边不多于 11 条，且不存在自环）. 那么

（1） GG 有一个度数最多是 55 的顶点.

（2） GG 最多有 3n−63n-6 条边.

（3）若 GG 的边被两种颜色着色，那么存在一个顶点，围绕此点的边沿圆环次序，最多经历两次颜色变化.

证明 我们可以假设 GG 是连通的（任意两顶点都有路径相连）.

（1）由于 GG 是简单的， GG 的每一面至少有 33 条边. 那么， f=f3+f4+f5+⋯f=f_3+f_4+f_5+\cdots ，且 2e=3f3+4f4+5f5+⋯2e=3f_3+4f_4+5f_5+\cdots ，故 2e−3f≥02e-3f\ge0 .

如果每个顶点度数至少是 66 ，那么， n=n6+n7+n8+⋯n=n_6+n_7+n_8+\cdots ，且 2e=6n6+7n7+8n8+⋯2e=6n_6+7n_7+8n_8+\cdots ，故 2e−6n≥02e-6n\ge0 .

这样，我们有 6(e−n−f)=2e−6n+2(2e−3f)≥06(e-n-f)=2e-6n+2(2e-3f)\ge0 ，即 e≥n+fe\ge n+f ，这和欧拉公式 e=n+f−2e=n+f-2 矛盾.

（2）由于 2e−3f≥02e-3f\ge0 ，根据欧拉公式， 3n−6=3e−3f≥e3n-6=3e-3f\ge e .

（3）令 cc 为颜色发生变化的角的数量. 假设命题不成立，由于围绕一个顶点的边的颜色变化次数是偶数，我们有 c≥4nc\ge4n . 每个有 2k2k 或 2k+12k+1 条边的面最多有 kk 个颜色发生变化的角，所以 4n≤c≤2f3+4f4+4f5+6g6+6f7+⋯≤2f3+4f4+6f5+8g6+10f7+⋯4n\le c\le2f_3+4f_4+4f_5+6g_6+6f_7+\cdots \le2f_3+4f_4+6f_5+8g_6+10f_7+\cdots =2(3f3+4f4+5f5+⋯)−4(f3+f4+f5+⋯)=4e−4f=2(3f_3+4f_4+5f_5+\cdots)-4(f_3+f_4+f_5+\cdots)=4e-4f ，即 n≤e−fn\le e-f ，这和欧拉公式 n=e−f+2n=e-f+2 矛盾.

围绕一个顶点的边的颜色变化次数是偶数

3 西尔维斯特-加莱定理

西尔维斯特曾经提出一个数学问题，证明不存在不在同一条直线上的有限点集，使得任意一条经过其中两点的直线都经过第三个点。此问题被加莱解决，并被记录为西尔维斯特-加莱定理（Sylvester-Gallai theorem）。

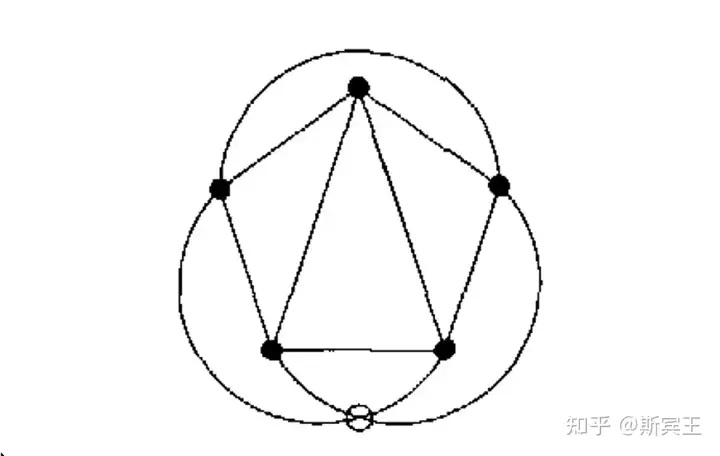
定理（西尔维斯特-加莱定理）给定平面上任意 n≥3n\ge3 个不共线的点，一定存在一条直线经过其中恰好两个点.

证明 把 R2\mathbb{R}^2 平面镶嵌到 R3\mathbb{R}^3 中单位球面 S2S^2 上. 那么 R2\mathbb{R}^2 中每个点对应 S2S^2 中一对对径点（antipodal points），且 R2\mathbb{R}^2 中每条直线对应 S2S^2 中一个大圆（great circle）. 这样，西尔维斯特-加莱定理可以转化为如下等价表述：给定球面上任意 n≥3n\ge3 对不共圆的对径点，一定存在一个大圆经过其中恰好两对对径点.

用球面中的对径点代表平面中的点，用球面中的大圆代表平面中的直线

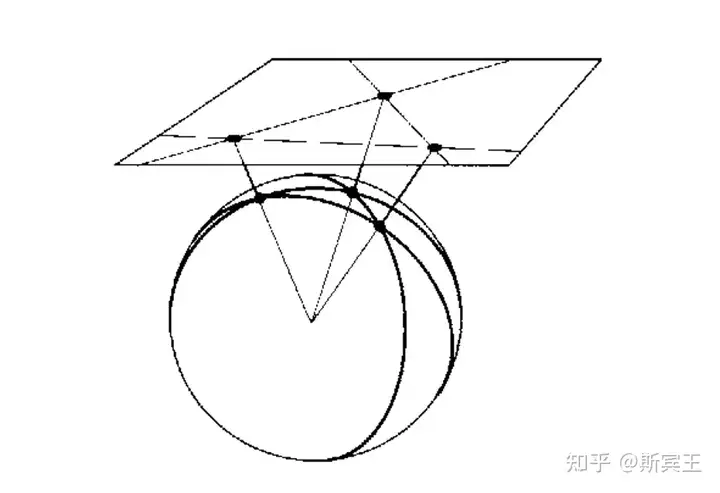
接着，对于每对对径点 ±v\pm v ，我们用与它们所决定的大圆的正交（orthogonal）圆 Cv={w∈S2:⟨v,w⟩=0}C_v=\{w\in S^2:\langle v,w\rangle=0\} 来代替它们. 这样，西尔维斯特-加莱定理可以转化为另一个等价表述：给定球面上任意 n≥3n\ge3 个不共点的大圆，一定存在一个点其中恰好在两个大圆上.

用正交圆代表对径点

将球面 S2S^2 中大圆交点视作顶点，大圆的连接两个交点的部分视作边，我们得到了一个简单平面图. 根据构造，顶点的度数都是偶数，且至少是 44 . 注意，度数为 44 时，顶点恰好在两个大圆上. 根据欧拉公式局部推论的第一个结论，存在一个度数为 44 （最多为 55 ）的顶点.

4 单色线

西尔维斯特-加莱定理关于着色的变式是由Chakerian给出的。

定理 给定平面上任意有限个黑色和白色的不共线的点，一定存在一条单色线（monochromatic line），即经过至少两个同色的点，而不经过另一颜色的点的线.

单色线

证明 类似于西尔维斯特-加莱定理的证明，我们将此定理转换为：给定球面上任意有限个黑色和白色的不共点的大圆，一定存在一个点，只落在白色的大圆上，或只落在黑色的大圆上.

据欧拉公式局部推论的第三个结论，一定存在一个经历 00 次颜色变化的顶点（最多 22 次），因为作为不同颜色的大圆交点的顶点，经历的颜色变化至少是 44 次.

5 皮克定理

皮克定理（Picks theorem）是一个计算多边形（polygon）面积的实用工具，它也是欧拉公式的一个推论。

定理（皮克定理）顶点坐标是整数的多边形 P⊆R2P\subseteq\mathbb{R}^2 的面积是 A(P)=nint+12nbd−1A(P)=n_{\mathrm{int}}+\frac{1}{2}n_{\mathrm{bd}}-1 .

证明 步骤 1 我们首先证明，顶点坐标是整数的三角形 T=conv{p0,p1,p2}⊆R2T=\mathrm{conv}\{p_0,p_1,p_2\}\subseteq\mathbb{R}^2 是 A(T)=12A(T)=\frac{1}{2} .

以 p0,p1,p2,p1+p2−p0p_0,p_1,p_2,p_1+p_2-p_0 为顶点的平行四边形（parallelogram） RR 和格（lattice） Z2\mathbb{Z}^2 对于映射 σ:x↦p1+p2−x\sigma:x\mapsto p_1+p_2-x 是对称的. 此映射是关于 p1,p2p_1,p_2 连线中点的反射（reflection），所以平行四边形 R=T∪σ(T)R=T\cup\sigma(T) 的顶点坐标也是整数. 此外，平行四边形的整点平移（integral translate）可以铺满整个平面.

由三角形通过反射构成平行四边形

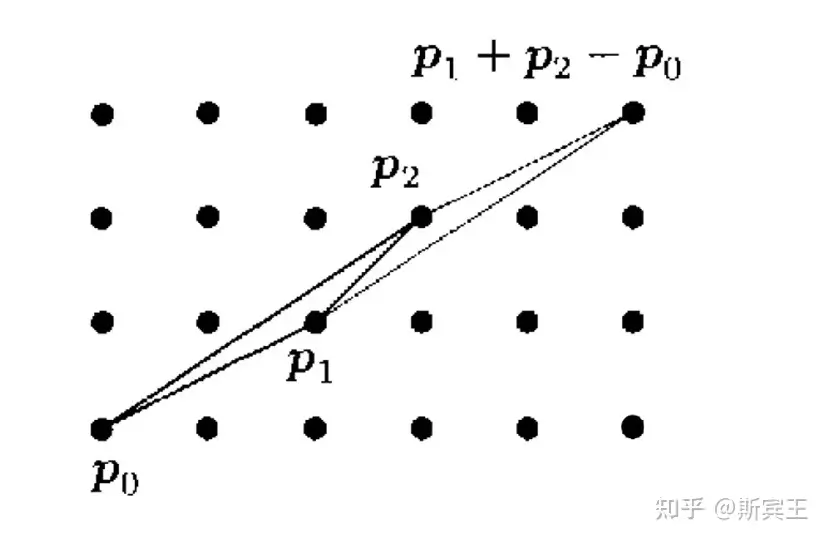
格 Z2\mathbb{Z}^2 的基底（basis）是一对线性独立（linearly independent）的向量 e1,e2e_1,e_2 ，使得 Z2={λ1e1+λ2e2:λ1,λ2∈Z}\mathbb{Z}^2=\{\lambda_1e_1+\lambda_2e_2:\lambda_1,\lambda_2\in\mathbb{Z}\} . 由 e1,e2e_1,e_2 生成的平行四边形的面积是 A(e1,e2)=|det(e1,e2)|A(e_1,e_2)=|\det(e_1,e_2)| ，而所有由基底生成的平行四边形的面积都是 11 . 由于平行四边形 RR 的整点平移可以铺满整个平面， {p1−p0,p2−p0}\{p_1-p_0,p_2-p_0\} 是格 Z2\mathbb{Z}^2 的一个基底. 那么 A(R)=1A(R)=1 ，也就是说， A(T)=12A(T)=\frac{1}{2} .

步骤 2 我们接下来证明，任一多边形都存在三角剖分，即 PP 可以由内部的和边界的格点分成小三角形.

当 n=3n=3 时，多边形是三角形，所以无需证明.

当 n≥4n\ge4 ，我们只需找到一条对角线，将多边形分为两部分，因为根据归纳假设，每部分都可以被三角剖分，也就是说，整个多边形可以被三角剖分.

若一顶点内角小于 180∘180^\circ ，则称此顶点是凸的. 由于 nn 边形内角和为 (n−2)180∘(n-2)180^\circ ，根据鸽笼原理（pigeonhole principle），任意 nn 边形至少存在 33 个凸顶点.

任取一凸顶点 AA ，并考虑其相邻顶点 B,CB,C . 若线段 BCBC 在 PP 中，则线段 BCBC 就是我们所需的对角线. 若线段 BCBC 不在 PP 中，则三角形 ABCABC 包含其他顶点. 将 BCBC 向 AA 平移，会碰到最后一个顶点 ZZ . 连接 AZAZ ，我们也可以得到所需的对角线.

寻找所需的对角线

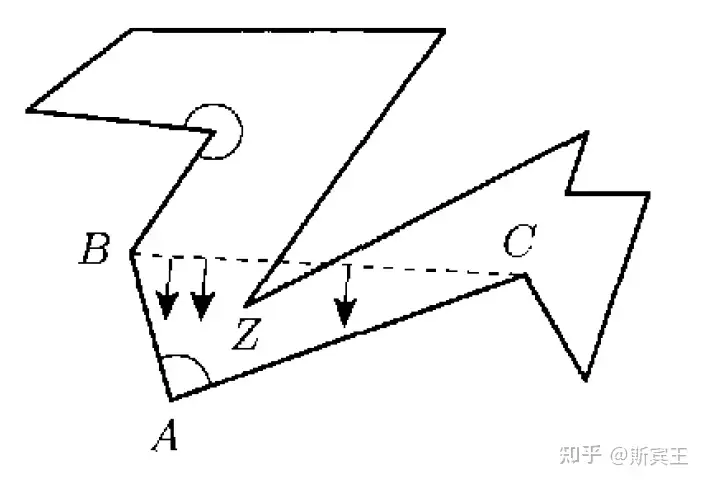
步骤 3 我们用三角剖分和 A(T)=12A(T)=\frac{1}{2} 来证明 A(P)=nint+12nbd−1A(P)=n_{\mathrm{int}}+\frac{1}{2}n_{\mathrm{bd}}-1 .

将三角剖分视作一个平面图，我们有 11 个无边界的面和 f−1f-1 个面积是 12\frac{1}{2} 的三角形，故 A(P)=12(f−1)A(P)=\frac{1}{2}(f-1) .

多边形的三角剖分

每个三角形有 33 条边，且 einte_\mathrm{int} 条内部边的每一条是两个三角形的边界，而 ebde_\mathrm{bd} 条边界边的每一条是一个三角形的边界，所以 3(f−1)=2eint+ebd3(f-1)=2e_\mathrm{int}+e_\mathrm{bd} ，故 f=2(e−f)−ebd+3f=2(e-f)-e_\mathrm{bd}+3 . 另外，边界上的顶点数等于边数，即 nbd=ebdn_\mathrm{bd}=e_\mathrm{bd} .

根据欧拉公式， f=2(e−f)−ebd+3=f=2(n−2)−nbd+3=2nint+nbd−1f=2(e-f)-e_\mathrm{bd}+3=f=2(n-2)-n_\mathrm{bd}+3=2n_\mathrm{int}+n_\mathrm{bd}-1 ，所以 A(P)=12(f−1)=nint+12nbd−1A(P)=\frac{1}{2}(f-1)=n_{\mathrm{int}}+\frac{1}{2}n_{\mathrm{bd}}-1 .

参考文献

[I] G. D. Chakerian. Sylvesters problem on collinear points and a relative, Amer. Math. Monthly 77 (1970), 164-167.

[2] G. Pick. Geometrisches zur Zahlenlehre, Sitzungsberichte Lotos (Prag), Natur-med. Verein fur Bohmen 19 (1899), 311-319).

[3] K. G. C. Von Staudt. Geometrie der Luge, Verlag der Fr. Kornschen Buchhandlung, Nurnberg 1847.

[4] N. E. Steenrod. Solution 4065/Editorial Note, Amer. Math. Monthly 51 (1944), 170-171.

[5] Martin Aigner, Gutner M. Ziegler. Proofs from the Book.