PageRank的简单理解-什么是pagerank算法
前言
PageRank 算法
是 Google 创始人于1997年构建早期的搜索系统原型时提出的链接分析算法,是 Google 用于用来标识网页的等级/重要性的一种方法,是 Google 用来衡量一个网站的好坏的唯一标准。例如:一个 PR 值为1的网站表明这个网站不太具有流行度,而 PR 值为7到10则表明这个网站非常受欢迎(或者说极其重要)。一般 PR 值达到4,就算是一个不错的网站了。
如果跳出网页推荐这一具体应用来看,我们可以将网页看成图中的节点,进而可以将PageRank 看成是图分析中的重要算法。在实际应用中许多数据都以图(graph)的形式存在,比如,互联网、社交网络都可以看作是一个图。图数据上的机器学习具有理论与应用上的重要意义。 PageRank 是图的链接分析(link analysis)的代表性算法,属于图数据上的无监督学习方法。
1. 什么是 PageRank
PageRank 算法的基本想法是在有向图上定义一个随机游走模型,即一阶马尔可夫链,描述随机游走者沿着有向图随机访问各个结点的行为。在一定条件下,极限情况访问每个结点的概率收敛到平稳分布,这时各个节点的平稳概率值就是其 PageRank 值,表示结点的重要度。PageRank 是递归定义的,可以通过迭代算法进行。
假设互联网是一个有向图,在其基础上定义随机游走模型,即一阶马尔可夫链,表示网页浏览者在互联网上随机浏览网页的过程。假设浏览者在每个网页依照连接出去的超链接以等概率跳转到下一个网页,并在网上持续不断进行这样的随机跳转,这个过程形成一阶马尔可夫链。PageRank 表示这个马尔可夫链的平稳分布。每个网页的 PageRank 值就是平稳概率。
2. PageRank 算法推导
PageRank 的提出是为了解决基于网页的搜索推荐问题,它的提出基于两个假设,分别是数量假设 和 质量假设。
数量假设:在网页模型图中,一个网页接收到的其他网页指向的入链(in-links)越多,说明该网页越重要。
质量假设:当一个质量高的网页指向(out-links)一个网页,说明这个被指向的网页质量也高。
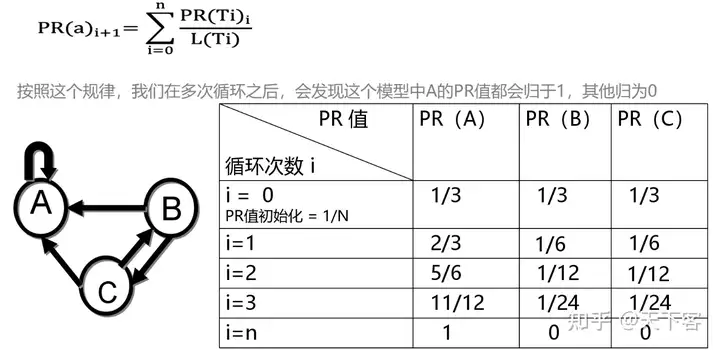
基于此,我们给出迭代的计算每个网页(节点)的 PR 值计算公式:
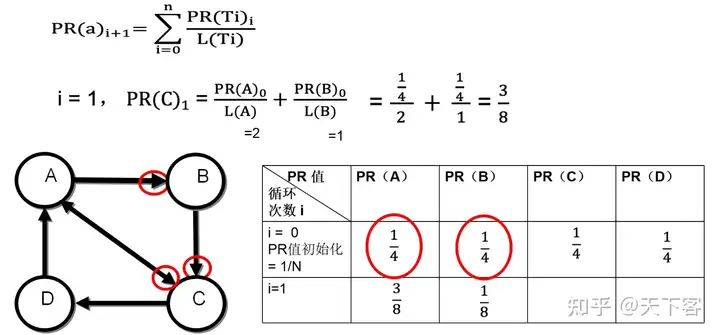
(1)PR(a)i+1=∑i=0nPR(Ti)iL(Ti)PR(a){i+1} = \sum{i = 0}^n \frac{PR(T_i)_i}{L(T_i)} \tag{1}
其中, PR(Ti)iPR(T_i)_i 代表的是在第 ii 次迭代中其他节点(指向节点a的节点)的PR值, L(Ti)L(T_i) 代表的是其他节点(指向节点a的节点)的出链数。(数量假设和质量假设)
在算法开始迭代之前,初始化每一个网页(图中节点)的 PR 值,一般情况下,所有结点的 PR 值初始化为 1N\frac{1}{N} ,其中 N N 为所有网页的数量。
基于此,我们可以看出 PageRank 其实是一种无监督的迭代算法,基于网页之间已知的超链接跳转关系可以不断迭代计算每个网页的重要程度直至收敛。
3. PageRank 的矩阵化分析
前面说过 PageRank 算法的基本思想是在有向图上定义一个随机游走模型,即一阶马尔可夫链,描述随机游走者沿着有向图随机访问各个结点的行为。这个随机游走模型即一阶马尔可夫链的详细定义如下,可以辅助理解 PageRank 的矩阵化推导。
随机游走模型(一阶马尔可夫链):
给定一个含有 nn 个节点的有向图,在有向图上定义随机游走(random walk)模型,即一阶马尔可夫链,其中节点表示状态,有向边表示状态之间的转移,假设从一个节点到通过有向边相连的所有节点的转移概率相等。具体地,转移矩阵是一个 nn 阶矩阵。
(2)M=[mij]n×nM = [m_{ij}]_{n \times n} \tag{2}
第 ii 行第 jj 列的元素 mijm_{ij} 取值规则如下:如果节点 jj 有 k k 个有向边连出,并且节点 i i 是其连出的一个节点,则 mij=1km_{ij} = \frac{1}{k} ,否则 mij=0,i,j=1,2,…,n m_{ij} = 0,i,j=1,2,\dots,n 。
转移矩阵 M M 具有如下性质
(3)mij≥0m_{ij}\ge0\tag{3}
(4)∑i=1nmij=1\sum_{i = 1}^nm_{ij} = 1\tag{4}
每个元素非负,每列元素之和为 1。即 转移矩阵 MM 为随机矩阵(stochastic matrix)。
在有向图上的随机游走形成马尔可夫链。也就是说,随机游走者每经一个单位时间转移一个状态,如果当前时刻在第 jj 个结点(状态),那么下一个时刻在第 i i 个结点(状态)的概率是 mijm_{ij} 这一概率只依赖于当前的状态,与过去无关,具有马尔可夫性。
PageRank 的矩阵化分析
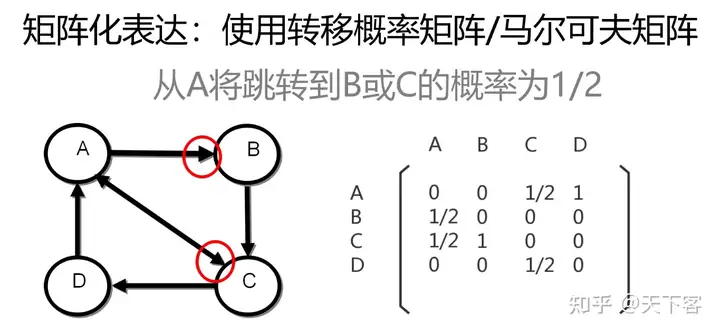
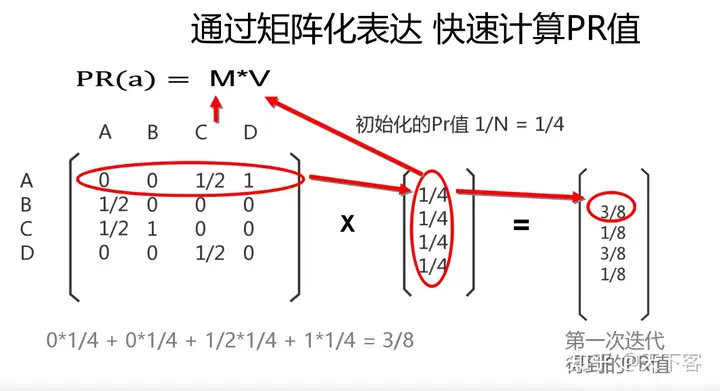
其中 PR(a)=M∗VPR(a) = M * V 中 MM 是根据网页之间的连接关系得到的一阶马尔可夫矩阵, VV 是每一次迭代计算出的每个网页的 PR 值。
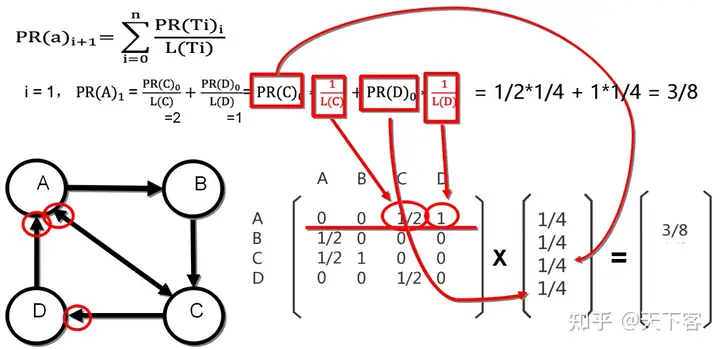
4. PageRank 可能存在的问题
问题一:Dead Ends
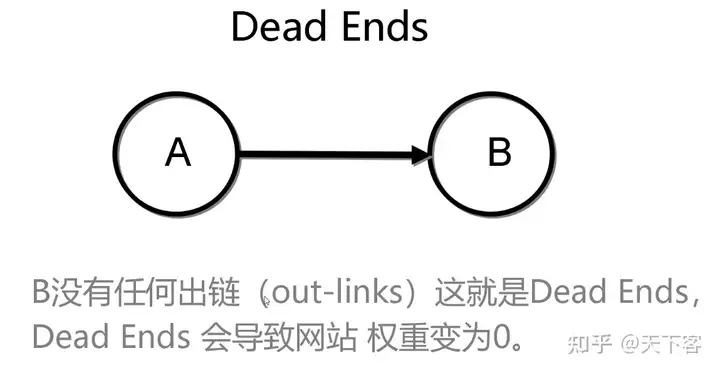
Dead Ends 问题的修正
Teleport——将节点图转化成列转移概率矩阵,再修正马尔科夫矩阵M :
(5)PR=(M+aT(en)∗V)PR = (M+a^T(\frac{e}{n})*V)\tag{5}
a=[a0,a1,…,an]a = [a_0,a_1,\dots,a_n] ,当有一列全为 0 时(该节点无出链),替换为 ai=1 a_i = 1 ee 为由 1 填满的列矩阵nn 为 M M 矩阵的行数/列数VV 为 PR 值矩阵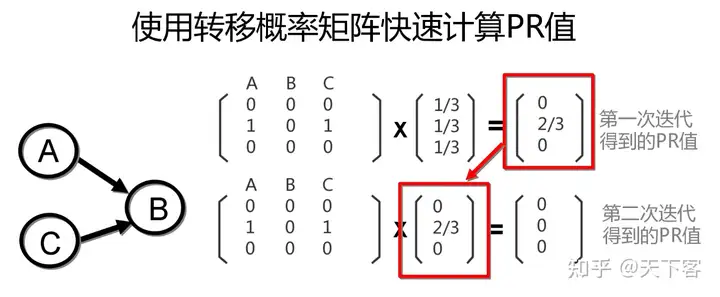
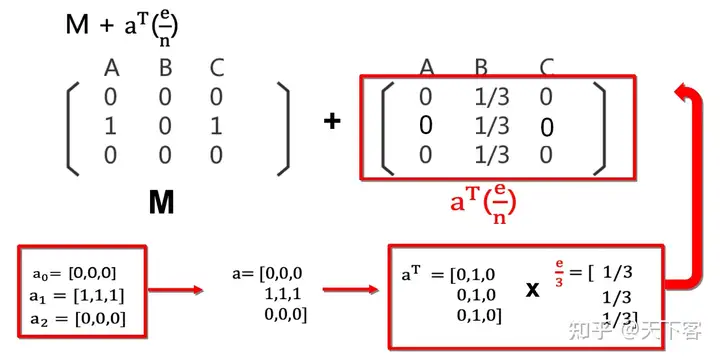
问题二:Spider Traps
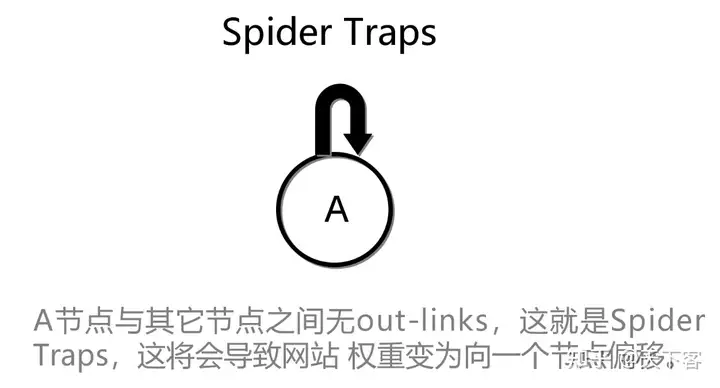
Spider Traps 问题的修正
Random Teleport——将节点图转化成列转移概率矩阵,再修正马尔科夫矩M(随机浏览模型) :
(6)PR=[βM+(1−β)eeTn]∗VPR = [\beta M+(1-\beta)\frac{ee^T}{n}]*V\tag{6}
nn 为概率转移矩阵 MM 的行数/列数β\beta 表示跟随出链(out-links)打开网页的概率1−β1-\beta 表示随机跳到其他网页的概率,例如:浏览 a 的时候有一定概率打开 b 和 ceeTee^T 表示由 1 填满的 n×n n \times n 矩阵VV 表示 PR 值的矩阵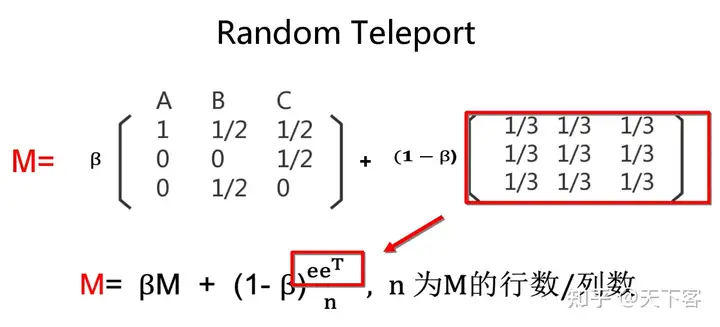
5. PageRank 的优缺点
优点
(1)通过网页之间的链接来决定网页的重要性,一定程度消除了对认为排名结果的影响;
(2)离线计算PageRank值,提升了查询效率。
缺点
(1)存在时间长的网站,PageRank值会越来越大(因为其入链会越来越多);新生的网站,PageRank值增长慢(因为其初始入链相对较少且增长慢);
(2)非查询相关的特性,查询结果会偏离搜索内容;
(3)可以通过“僵尸网站”或链接,人为刷PageRank值;
6. 参考
算法通俗易懂
以上就是关于《PageRank的简单理解-什么是pagerank算法》的全部内容,本文网址:https://www.7ca.cn/baike/18732.shtml,如对您有帮助可以分享给好友,谢谢。
