拉普拉斯变换速通（拉普拉斯变换）

 

注：本文仅对工科应试有一定帮助，对您深入了解拉普拉斯变换毫无用途拉普拉斯变换的定义： L[f(t)]=∫0+∞f(t)estdt=F(s)\mathcal L[f(t)]=\int_0^{+\infty}f(t)e^{st}\mathrm dt=F(s)。

，其中 t≥0t\ge0 .给出以下常用变换：

拉普拉斯变化是一个线性变换eg1:计算 f(t)=t2−2t+1f(t)=t^2-2t+1 的拉普拉斯变换L[t2−2t+1]=L[t2]−2L[t]+L[1]=2!s3−2⋅1s2+1s\mathcal L[t^2-2t+1]=\mathcal L[t^2]-2\mathcal L[t]+\mathcal L[1]=\frac{2!}{s^3}-2\cdot\frac 1{s^2}+\frac1s。

eg2:证明公式8.L[f′]=limb→∞∫0bf′(t)e−stdt=limb→∞[f(t)e−st+∫sf(t)estdt]t=0t=b\mathcal L[f]=\lim _{b\to\infty}\int_0^bf(t)e^{-st}\mathrm d t= \lim _{b\to\infty}[f(t)e^{-st}+\int sf(t)e^{st}\mathrm dt]_{t=0}^{t=b}

=limb→∞[f(b)e−sb−f(0)]+slimb→∞∫0bf(t)e−stdt=−f(0)+sL[f]=\lim _{b\to\infty}[f(b)e^{-sb}-f(0)]+s\lim _{b\to\infty}\int_0^bf(t)e^{-st}\mathrm dt=-f(0)+s\mathcal L[f]

推广至n阶导数有： L[f(n)]=snL[f]−sn−1f(0)−sn−2f′(0)−⋯−f(n−1)(0)\mathcal L[f^{(n)}]=s^n\mathcal L[f]-s^{n-1}f(0)-s^{n-2}f(0)-\cdots-f^{(n-1)}(0)

拉普拉斯逆变换： f(t)=L−1[F]=12πi∫c−i∞c+i∞F(s)estdsf(t)=\mathcal L^{-1}[F]=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(s)e^{st}\mathrm ds

实际运用中把右边的往左边对着看就行，至于怎么证明，我不会（理直气壮）eg3:求解 x″−x=1,x(0)=1,x′(0)=2x-x=1, x(0)=1,x(0)=2s2L[x]−s−2−L[x]=1ss^2\mathcal L[x]-s-2-\mathcal L[x]=\frac 1s

L[x]=1s+1−1s+1s+1\mathcal L[x]=\frac1{s+1}-\frac1s+\frac1{s+1} ,运用逆变换就可以得到 x(t)=2e−t−1x(t)=2e^{-t}-1 .

s位移性质：若有 L[f(t)]=F(s)\mathcal L[f(t)]=F(s) ，则有 L[e−atf(t)]=F(s+a)\mathcal L[e^{-at}f(t)]=F(s+a)或者说 L−

1[F(s+a)]=e−atf(t)\mathcal L^{-1}[F(s+a)]=e^{-at}f(t)eg4:求 g(t)=e−4tt2g(t)=e^{-4t}t^2 的拉普拉斯变换.套公式就行：

L[g]=2!(s+4)3\mathcal L[g]=\frac{2!}{(s+4)^3}eg5: 求F(s)=4s−12s2−6s+18F(s)=\frac{4s-12}{s^2-6s+18} 的逆变换；

F(s)=4(s−3)(s−3)2+9=L[e3tg(t)]F(s)=\frac{4(s-3)}{(s-3)^2+9}=\mathcal L[e^{3t}g(t)]查表得 L−1[F(s)]=4e3tcos

⁡3t\mathcal L^{-1}[F(s)]=4e^{3t}\cos3tt位移定理：若 ff 拉普拉斯变换为 FF ，则 g(t)={0t

的拉普拉斯变换为 L[g(t)]=e−asF(s)\mathcal L[g(t)]=e^{-as}F(s) （其中 0">a>0a>0 )单位阶跃函数：u(t−a)={0t

（要求 a≥0a\ge0 ）图像就是这个样子：

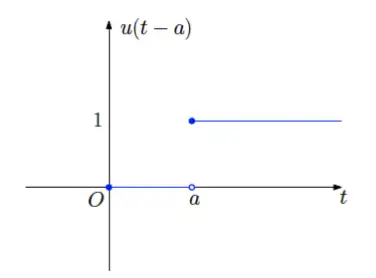
这样我们就有 L[f(t−a)u(t−a)]=e−asF(s)\mathcal L[f(t-a)u(t-a)]=e^{-as}F(s)或者： L[e−asF(s)]=f(t−a)u(t−a)\mathcal L[e^{-as}F(s)]=f(t-a)u(t-a)

eg6: G(s)=e−2ss5G(s)=\frac{e^{-2s}}{s^5} ，求其逆变换套公式即有 L−1[G(s)]=u(t−2)⋅(t−2)44!\mathcal L^{-1}[G(s)]=u(t-2)\cdot\frac{(t-2)^4}{4!}

eg7:求 g(t)={20≤t<π0π≤t<2πsin⁡tt≥2πg(t)=\begin{cases} 2&0\le t<\pi\\ 0&\pi\le t<2\pi\\ \sin t&t\ge2\pi \end{cases}

的拉普拉斯变换.这个函数是分三段的，但是我们可以用多段单位阶梯函数把它们一段一段“拼”起来，如下图：

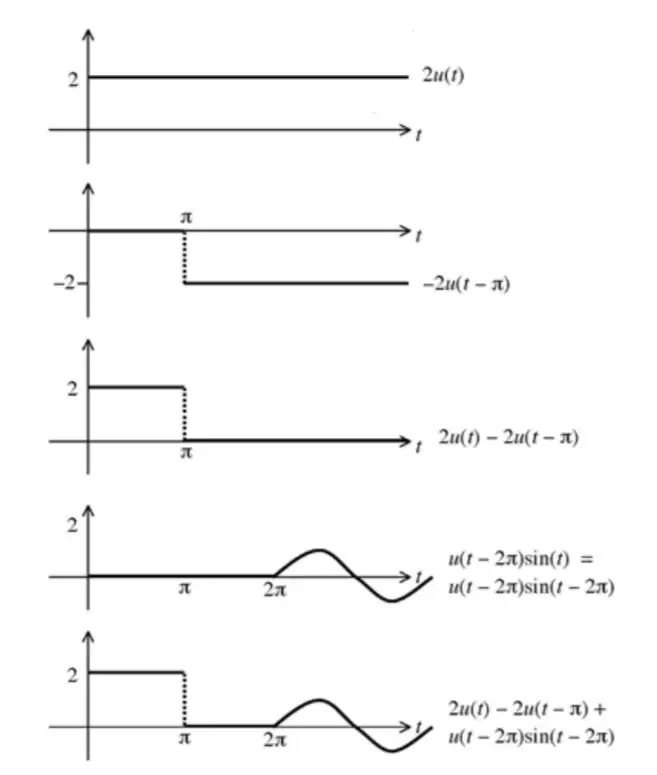
最后就变为求 g(t)=2u(t)−2u(t−π)+u(t−2π)sin⁡(t−2π)g(t)=2u(t)-2u(t-\pi)+u(t-2\pi)\sin(t-2\pi) 的拉普拉斯变换，这就非常容易了。

脉冲:对任意 a≥0a\ge0 与 0">ϵ>0\epsilon>0 ，令 fϵ(t−a)={1ϵa≤t≤a+ϵ0otherwisef_{\epsilon}(t-a)=\begin{cases} \frac1{\epsilon}&a\le t\le a+\epsilon\\ 0 &otherwise \end{cases}

图像就是这样：

脉冲 Iϵ=∫0∞fϵ(t−a)dt=1I_{\epsilon}=\int_0^{\infty}f_{\epsilon}(t-a)\mathrm dt=1 .狄拉克δ\delta函数：a≥0a\ge0

， δ(t−a)=limϵ→0fϵ(t−a)={0t≠a∞t=a\delta(t-a)=\lim_{\epsilon\to0}f_{\epsilon}(t-a)=\begin{cases} 0&t\neq a\\ \infty&t=a \end{cases}

然后有 ∫0tδ(τ−a)dτ=u(t−a)={0t

.∫0tδ(τ−a)dτ=1\int_0^t\delta(\tau-a)\mathrm d\tau=1 .对积分上限函数进行拉普拉斯变换：若 L[f(t)]=F(s)\mathcal L[f(t)]=F(s)

，则有 L[∫0tf(t)dt]=F(s)s\mathcal L[\int_0^tf(t)\mathrm dt]=\frac{F(s)}seg8: y(t)−∫0ty(τ)dτ=3y(t)-\int_0^ty(\tau)\mathrm d\tau=3

,求 y(t)y(t) .不妨设 L[y]=F(s)\mathcal L[y]=F(s) ，则有 F(s)−F(s)s=3sF(s)-\frac{F(s)}s=\frac3s .F(s)=3s−1F(s)=\frac3{s-1}

, y=3ety=3e^t .（拉普拉斯）卷积： 我们规定函数 ff 与 gg 的（拉普拉斯）卷积为 (f∗g)(t)=∫0tf(τ)g(t−τ)dτ(f*g)(t)=\int_0^tf(\tau)g(t-\tau)\mathrm d\tau

.其符合交换律： f∗g=g∗ff*g=g*f (利用区间再现).（拉普拉斯）卷积定理：若 L[f(t)]=F(s)\mathcal L[f(t)]=F(s) ， L[g(t)]=G(s)\mathcal L[g(t)]=G(s)

，则 L[(f∗g)(t)]=F(s)G(s)\mathcal L[(f*g)(t)]=F(s)G(s)或者 (f∗g)(t)=L−1[F(s)G(s)](f*g)(t)=\mathcal L^{-1}[F(s)G(s)]

.eg9:求 F(s)=1(s+1)(s−3)F(s)=\frac1{(s+1)(s-3)} 的拉普拉斯逆变换.L−1[1s+1]=e−t\mathcal L^{-1}[\frac1{s+1}]=e^{-t}

, L−1[1s−3]=e3t\mathcal L^{-1}[\frac1{s-3}]=e^{3t}由卷积定理： L−1[1(s+1)(s−3)]=∫0tf(τ)g(t−τ)dτ=∫0te−τe3(t

−τ)dτ\mathcal L^{-1}[\frac1{(s+1)(s-3)}]=\int_0^tf(\tau)g(t-\tau)\mathrm d\tau=\int_0^te^{-\tau}e^{3(t-\tau)}\mathrm d\tau

=e3t∫0te−4τdτ=−14e−t+14e3t=e^{3t}\int_0^te^{-4\tau}\mathrm d\tau=-\frac14e^{-t}+\frac14e^{3t}