真实的谎言——辛普森悖论面面观（辛普森悖论实例）

 

世界上有三种谎言：谎言、可恶的谎言和统计数据。——马克•吐温

马云曾经在一次演讲中说道：“人类正从IT时代走向DT时代”。

IT，我们已经非常熟悉了，英文Information Technology的缩写，即信息技术。

DT，是英文Data Technology的缩写，即数据技术。DT是对数据进行存储、清洗、加工、分析、挖掘，从数据中发掘规律的技术。DT技术让我们能够借助计算机的计算能力认知这个世界，提升我们认知的同时，影响我们思考、帮助我们决策。DT技术是以服务大众、激发生产力为主的技术。DT时代，社会将以数据作为核心和内在驱动力。

在这个大时代里，大数据（Big Data）和海量资讯（Information）扮演着重要的角色。大数据相当于21世纪的石油，数据是新经济的燃料，未来最大的能源是数据。如果能够妥善应用大数据，我们可以拥抱更为美好的未来。政府和企业目前十分关注大数据、互联网产业，并把它们打造成经济发展新引擎。近些年来，随着大数据行业的蓬勃发展，数据驱动（Data-Driven）受到越来越多的追捧。越来越多场景的数据采集、越来越成熟的分析模型、越来越强大的分析效率，这些无疑都为我们精细分析、优化决策助益良多，是为数据智能。

然而在数据背后，往往隐藏着一些似是而非的谬误。

我们每天看到海量的资讯，在这些纷繁复杂的信息中，如何做出准确的判断，如何避免被误导，如何保持独立的思考，这些能力都显得无比重要。

数据驱动人生，数据决定一切。也许你会说，我只相信我的眼睛！我只相信数据！

真的是这样的吗？

你知不知道，数据也会说谎？

就像我说，马化腾真有钱，我和刘强东加起来还没有他多；我和马化腾的平均财富超过了2000亿……你相信吗？实质是，我搬砖的收入远远不够还债……

不说谎的数据也能欺骗人，这是真实的谎言。

今天，我们一起来聊一聊统计数据中的辛普森悖论。

1

多歧路，今安在？

——李白《行路难》

如果我给你一组数据——一中的高考升学率为75%，二中的升学率为70%，你会把你的孩子送到哪个学校读书呢？

参加高考全部人数升学率

参加高考人数升学人数升学率一中100075075%二中100070070%

当然是一中了！

对不起，也许你选错了！看一看下面这两张表。

理科高考升学率

参加高考人数升学人数升学率一中80070087.5%二中50045090.0%

文科高考升学率

参加高考人数升学人数升学率一中2005025.0%二中50025050.0%

虽然一中的总体升学率高于二中，但是不管是文科升学率还是理科升学率，一中都没有二中高！

不会吧？

揉揉眼睛再看一看。你没看错，数据就是这么神奇！

数据可不会是骗人的，不信可以自己动手验算一下，真的出现了这种违背常理的情况！

可能有些人还是一头雾水，虽然数据是如此没错，可还是不能理解到底发生了什么，这个结论如此古怪！

难道数据有魔法？

这其实就是著名的辛普森悖论（Simpsons Paradox）：同一组数据，从整体和分组来看，得到的结果竟然截然相反！

2

拔剑四顾心茫然

——李白《行路难》

辛普森悖论在日常生活中司空见惯。为了便于理解，我们再举一个餐馆选择的实例。

选餐馆的时候，在手机软件上根据就餐者的点评选择两家餐厅就餐，发现餐馆A总体好评率高，但是B餐厅却在分别看男性和女性各组的评分中拔得头筹。该选哪一家呢？

人们逢年过节或朋友聚会常常会到餐馆聚餐。作为主人的你找了两家餐馆，感觉好像都不错，进一步通过手机软件了解餐馆的好评率调查。

如果A餐馆400名顾客中的好评率是80％，B餐馆400名顾客中的好评率是75％，想一想，你会选择哪一家餐馆消费呢？

A餐馆和B餐馆的总体好评率

总人数好评人数好评率A餐馆40032080%B餐馆40030075%

A餐馆分男女好评率统计

性别人数好评人数好评率男1006060%女30026087%整体40032080%

B餐馆分男女好评率统计

性别人数好评人数好评率男25016566%女15013590%整体40030075%

总体好评率80％＞75％，看起来应该毫不犹豫选择A餐馆。但是，如果进一步用性别分组，各自显示好评率瞧一瞧。男顾客对于B餐馆的好评率66％比A餐馆的60％高；女顾客对于B餐馆的好评率90％同样比A餐馆的87％高。以性别区分，不管怎么看都应该选择B餐馆，但以整体好评率来看却应选择A餐馆！

这是怎么一回事呢？

还是辛普森悖论在作怪！

3

闲来垂钓碧溪上

——李白《行路难》

辛普森悖论（Simpson’s Paradox）也称辛普森诡论，在统计学中亦有人称为“逆论”，甚至有人视之为“魔术”，即在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑（整体），却又不尽相同，甚至是完全相反的结论。

很早之前，George Udny Yule（1903）及Karl Pearson（1899）都曾撰文描述此现象。

1951年英国统计学家E.H.辛普森（Edward H. Simpson）发表了一篇论文，其中讨论到“两个类型变量之间的相关性，可能因为加入第三个类型变量而得到不同的结果”。后来就以他的名字命名该悖论。从此之后，辛普森悖论开始广为人知。

简而言之，根据您对数据的分析方式，相同的数据可能会产生相互矛盾的结果。这其中存在令人难以置信和违反直觉的现象。

辛普森悖论：同一组数据，整体的趋势和分组后的趋势完全不同。如下图所示，因变量y和自变量x的关系，在整体上看是正相关的；但是，当把数据拆开细看的时候（图中分为A、B、C三组），y和x却是负相关的。

数学上，假如下面这两个式子成立：

A / B> a / b

C / D> c / d

但是将它们分别加起来的比例式并非总是成立：

（A + C）/（B + D）>（a + c）/（b + d）

人们总是想当然或者直觉地认为这个和式成立，事实上，这是不对的。

当实际出现相关性反转时，即在分组比较中都占优势的一方，在总评中有时反而是失势的一方，这种现象就是所谓的“辛普森悖论”。其实，这里称为悖论是不准确的。这不是一个真正的悖论，它内部没有包含逻辑上的矛盾，而是复杂的系统所产生的有趣的现象，只是有些违背人们的常理罢了。

4

欲渡黄河冰塞川

——李白《行路难》

再来看一看举世瞩目的2016美国总统大选。特朗普和希拉里分别代表共和党和民主党角逐总统大位。

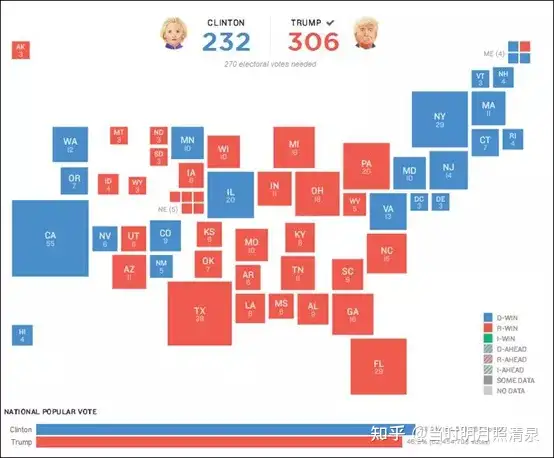
选票最终开票结果显示，希拉里在全美普选选票上大胜特朗普200多万张，但是最终问鼎白宫的却是特朗普。为什么低票数的人反而获得了选举的成功呢？

美国的选举制度并没有我们想象那么简单。

总统由各州选出的选举人团投票产生，选举人代表选民意愿投票。总统候选人获得超过半数选举人票（至少270张）即可获胜。美国大选一州为一个选举人团单位，根据“胜者全得”原则，美国全体选民在总统候选人之间投票，随后各州统计每名候选人在本州所获实际选票数，超过半数的候选人即获得本州全部选举人票（注：除缅因和内布拉斯加两个州是按普选票得票比例分配选举人票外，其余48个州和华盛顿特区均实行“胜者全得”制度）。在选举人票方面，希拉里仅仅拿下232张，远不及特朗普的306张。74张票的落差，让希拉里无力可回天。希拉里赢得比特朗普更多的民众投票。她获得了超过6500万张选票，是此前美国历史上总统大选第二多的选票，仅次于奥巴马。但因为特朗普赢得了30个州的胜利，在选举人团票上，特朗普却占据了优势，最终逆袭赢得大选。

我们看到，辛普森悖论现象在2016年美国大选上出现了。

5

忽复乘舟梦日边

——李白《行路难》

辛普森悖论主要两个体现：权重扭曲和遗漏变量。

简单看，之所以会出现辛普森悖论，是因为数据的总体和部分在结构上呈现了较大的差异，而且存在潜在变量或者混杂因素的影响。

例如，前面一中和二中升学率的实例中，文科和理科升学率有区别，文科生和理科生在一中和二中的比例有很大的差别。学生按照文科和理科分科，这里科别就是一个潜在变量。科别会影响学生比例，也会引起升学率的变化。

另一个餐馆选择的例子中，导致辛普森悖论的原因是因为两个餐馆男、女顾客比例相差很大，A餐馆的女顾客人数非常多，好评率也高，虽然B餐馆女顾客好评率略高，但以整体来说，A餐馆好评率还是会比较高。在这里，性别是一个潜在变量。

我们再来看一看。

假设我们调查了A、B 两个城市的房价，A 城市的均价为21000 元，B 城市的均价为16000 元，于是很快得出结论：A 城市的房价高于B 城市。

事实真是这样吗？

如果考虑到地段，发现A 城市大部分房子在内环，小部分在外环；而B 城市正好正好相反，内环只有少部分房子，大部分在外环。将A、B 两个城市的房价进一步按照地段划分，得到下面这张统计表。

A和B城房价统计

内环外环A城2300011000B城2500012000

可以看出：无论是内环还是外环，B 城市的房价都是高于A 城市，这与全样本分析结果刚好相反。数据分析人员经常会犯这样的错误，主要原因就是遗漏了潜在变量（关键变量、混杂因素），这里“地段”就是潜在变量。如果在将户型、是否学区房、是否靠近地铁变量考虑进去，还会得到其他的结论。

6

将登太行雪满山

——李白《行路难》

当辛普森悖论发生的时候，对潜在变量，特别是直接影响被解释变量的变量，一定要对其进行细分，然后才能得到正确的结论！否则结论往往可能是错的！

那么，发生辛普森悖论的时候，是不是我们就直接摒弃根据整体数据分析得到的结论呢？

不尽然。

看看下面的例子。

A在测试中连续赢得两场比赛。但是B的总分是否更高？

A和B在第一次和第二次共同解决100个问题的测验中相遇。

在第一次测试中，A先生的正确回答率为90％，B先生的正确回答率为80％。

在第二项测试中，A先生的正确回答率为50％，B先生的正确回答率为40％。

无论您如何看，它看起来都像A赢了。两次测试，2：0完胜！

但是，结论是很让人吃惊的。

如果仔细分析A和B两次测验的总体数据：

在第一次测试中，A正确率为90％（9/10个问题），B正确率为80％（72/90个问题）。

在第二个测试中，A的正确率为50％（45/90个问题），B的正确答案为40％（4/10个问题）。

如果将两个测试的分数相加，则A将获得54/100正确答案，B将获得76/100正确答案。

很明显，A在第一次和第二次的测验中都获得了胜利，但是总体数据却输给了B。辛普森悖论出现。

到底是A优秀还是B优秀呢？显然，这里要看整体数据，最终胜出的应该是B。

值得注意的是，这里第一次和第二次测试并不是一个潜在变量（混杂因素），因此，我们分析的时候要看整体数据。

7

长风破浪会有时

——李白《行路难》

如何避免辛普森悖论？

我们平时在选取数据分析数据的时候，一定要注意各组数据的权重（各组数据在整体评价中占的比例），以一定的系数去消除以分组资料基数差异所造成的影响，另外，还要留意该情景是否存在其它潜在变量的影响，仔细分析因果关系。

例如，一个有效的解决方法：对于占总体少数比例的样本加以更高的权重，也就是 “逆概加权”（Inverse probability weighting）。前面关于一中和二中升学率的例子，我们对每个子群体加权（理科和文科），权重为该子群体在总群体里出现的概率的倒数。

这样处理后，我们确实得出二中的升学率明显高于一中！

加权前升学率

理科文科升学率一中75%二中70%

加权后升学率

理科文科升学率一中56.25%二中70%

如果有潜在变量存在，牢记：整体数据未必可靠，要通过科学合理的分组来查看具体细致的数据。

辛普森悖论反映了数据结构局部和整体的差异，局部上的弱势在整体上并不代表就是劣势，有时可以以弱胜强，反败为胜。

有时候，我们却要考虑整体数据。

总之，辛普森悖论要求我们具备科学辩证思维，客观看待关联现象。

数据分析是一门技术，也是一门艺术。

8

行路难！行路难！

——李白《行路难》

辛普森悖论现象，放眼古今中外，还有我们的日常生活，举不胜数。

田忌赛马的故事家喻户晓：田忌的各个等级的马都不如齐威王，如何战胜齐威王？

孙膑献计田忌，用下等的马对齐威王的上等马，中等马对齐威王的下等马，上等马对齐威王的中等马，从而三局两胜赢了齐威王。

NBA的著名球星库里以擅射而闻名，但是有人却总结了库里与另一球星詹姆斯的若干场对战数据，发现库里的投篮命中率不及詹姆斯，因而质疑库里的神射之名。

事实上，虽然在这若干场比赛中，詹姆斯的总体投篮命中率是要高于库里的，但是无论是詹姆斯的两分球命中率，还是三分球命中率都要明显低于库里！库里之所以总的命中率低于詹姆斯，是因为其投了更多难度更大的三分球。库里射术精于詹姆斯，这不是浪得虚名，而是实至名归！

阿拉斯加航空公司在五个存在竞争的主要机场，拥有优于另一家航空公司的准点运行记录，但其总体准点记录则不如竞争对手，为什么？

因为阿拉斯加航空拥有许多飞往西雅图的航班，而西雅图的天气问题经常导致飞机延误。

2021年8月，根据英格兰公共卫生局（PHE）最近发布的一份报告，接种疫苗后死于COVID-19的人比未接种疫苗的人多，国外有网友在Facebook发文得出covid-19疫苗充分地增加了Delta感染者的住院死亡风险。

事实上，脸书此文对接种人群分析有误，英国的疫苗接种策略是首先为年龄较大、较脆弱的人接种疫苗，计算比例时忽略了数据的年龄组别，仅使用不分年龄的全体数字，由于不同年龄组别的接种比例有显著差异，导致辛普森悖论出现，令其得出与数据不符的结论。

对于每个年龄群体，瑞典的女性死亡率都要低于哥斯达黎加，但瑞典拥有更高的女性总体死亡率，为什么？

因为瑞典拥有更多的老年女性（老年人拥有相对较高的死亡率）。

一项医学研究发现，一种手术对于小型和大型肾结石的治疗成功率均高于另一种手术，但其总体成功率却不如另一种手术，为什么？

因为它经常被用于治疗大型肾结石（大型肾结石的治疗成功率相对较低）。

某大学录取率，女生整体录取率要显著低于男生，该大学的招生政策，是否存在性别歧视？到底是歧视男生还是女生？

仔细观察，女生录取率居然在每一个学院均高于男生录取率！造成这个现象的原因，是因为较多女性申请“录取率低的学院”。 打成都麻将的时候，把把都赢小钱，造成赢钱的假象，其实不如别人赢一把大的。

高校教师，B教师人称“许三多”：论文多项目多经费多，真的他就比A优秀吗？

你男票，这里比别人差，那里比别人差，但是其实他真的比别的男生差吗？

各种大学排行榜层出不穷，评价标准也是五花八门，但是你真的了解这些排行榜吗？还有各种别人家的孩子，别人家的老公，别人家的老婆…..

我们生活在各种各样的比较中：比高矮，比胖瘦，比快慢，比长短，比分数，比论文，比业绩，比职级，比薪水，比横向，比纵向，比总量，比人均，……然而很多人经常不知不觉中陷入各种不可自拔的比较的误区。

你在比较的同时，是否意识到，自己可能已经毫无察觉地掉进了辛普森陷阱……

人生苦短，何必计较太多！

只是芸芸世间俗人，往往难言洒脱！

叶倩文歌曲《真心真意过一生》

9

金樽清酒斗十千

——李白《行路难》

辛普森悖论很重要，因为它提醒我们，很多时候展示在我们面前的数据并非事实的全貌。经验告诉我们，数据从来都不是完全客观的！

数据是一个有力的武器，它既能被用来澄清现实，也能被用来混淆是非。

对那些不怀好意的人来说，他们很容易对数据进行拆分或者归总，得到一个对自己有利的指标，从而来迷惑甚至操纵他人。医学和社会学的研究者也常常会遇到辛普森悖论，从而得出错误的结论。

数据分析人员往往只关心数据，而忽视了数据产生的过程（因果）：数据是如何产生的？有哪些我们没看到的因素在影响结果？

一旦我们理解了数据生成的机制，我们就可以寻找影响结果的其他因素，跳出数据之外看数据，而统计图表一般不会告诉你这些。

很多时候，我们选择相信直觉，因为我们的直觉往往很准。但是，在信息不全或者信息非对称的情况下，直觉常常是是值得怀疑的。

我们应当使用理性而迟缓的思考，挖掘数据更深层次的东西：是否有漏掉重要因素或是错误归因的可能，用因果关系去理解数据，区分现象与本质，不要只看事物的表面。

辛普森悖论的出现是因为人们忽略了研究的因果关系；当因果关系变得明确时，这些看似自相矛盾的现象就会自动消失。也因此，数据分析者需要具有足够的背景知识，以便正确地识别问题的因果结构，最终做出明智的决策。

学会思考因果关系并建立思维模型，对现象进行正确的解读，对防止我们从数字中得出错误或者片面的结论至关重要。只有这样，我们在工作中才能具有明辨是非的能力，生活中也可以减少被骗、吃亏上当的可能性。

最近，因果关系在学术界也掀起了研究高潮。

朱迪亚·珀尔（Judea Pearl）是一名以色列裔美籍计算机科学家和哲学家，以倡导人工智能（AI）的概率方法和贝叶斯网络的发展而闻名，被称为贝叶斯网络之父。他还因在结构模型的基础上发展出因果和反事实推论而受到广泛称赞。2011年，国际计算机协会（ACM）授予Judea Pearl图灵奖，以表彰他“通过发展概率和因果推理演算对人工智能做出的基础性贡献”。图灵奖是计算机领域的国际最高奖项，被誉为“计算机界的诺贝尔奖”。Judea Pearl 期望能掀起一场“因果革命”，采用因果推理模型，从因果而非单纯的数据关联角度去研究人工智能。Judea Pearl认为因果推理有助于实现强人工智能。

约书亚·本吉奥（Yoshua Bengio）因深度学习工作与Geoffrey Hinton和Yann LeCun共同分享了2018年图灵奖，被公认为世界领先的人工智能专家和深度学习先驱。正是深度学习技术掀起了人工智能的复兴浪潮，也一步步推动了无人驾驶汽车、即时语音翻译以及人脸识别成为可能。最近，本吉奥认为深度学习擅长在大量数据中发现模式，但无法解释它们之间的联系。他指出深度学习已经走到了瓶颈期，如果无法推理出因果关系，人工智能就无法接近人类的智力水平，“将因果关系整合到AI当中已经成为目前的头等大事”。

美国经济学家乔舒亚·D·安格里斯特（Joshua D. Angrist）和吉多·W·因本斯（Guido W. Imbens），因为在因果关系分析方面的方法论的卓越贡献，荣膺2021年诺贝尔经济学奖。David Card把因果推断应用于劳动经济学，研究了教育年限对收入的影响，与他们分享了该奖项。

计算机和人工智能学界关于因果关系的创新研究，加之今年相关成果又荣获诺贝尔经济学奖，无疑，因果关系异常瞩目！

10

直挂云帆济沧海

——李白《行路难》

辛普森悖论这种“整体趋势与个别趋势不同”的现象，其原因本质上其实非常简单：我们一般在分析数据的时候，要考虑“质”和“量”两个维度，量与质往往是不等价的，无奈的是量比质来得容易量测，所以人们总是习惯用量来评定好坏。

说得再直白一点就是，我们在求“平均”的时候没有自觉考虑权重。

数据是一个有力的武器，它既能被用来澄清现实，也能被用来混淆是非。

统计数据需要谨慎对待，如果处理不慎，统计数据显示的情况可能与事实相悖。

人生思考：当个人各项能力都比其他人差的时候，并不一定总体劣于对手；当个人总体能力比别人强的时候，注意深思单项能力可能居于劣势。

总之，数据并不是魔法！只要洞悉数据背后隐藏的秘密，一切悖论必将迎刃而解！

关注我的微信公众平台，请搜索“当时明月照清泉”。