关于sin10°，cos10°值的求法-如何求tan15°的值

 

我们可以通过一些特殊的方法计算出某些特殊角度的三角函数值。

45°时的值：

在正方形中我们可以做出45°角并求出各边的长度分别为1,1和根号2/2，于是sin45°= 22\frac{\sqrt{2}}{2}

30°及60°的值：

通过几何手段我们可以构造出两个锐角分别为30°和60°的直角三角形并可以求出该三角形的三个边长分别为1,2和根号3，于是可求得sin30°= 12\frac{1}{2} cos30°= 32\frac{\sqrt{3}}{2}

再通过和差化积公式我们就得到了sin15°=sin（45°-30°）= (6−2)4\frac{\left(\sqrt{6} -\sqrt{2}\right)}{4} cos15°= (6+2)4\frac{\left(\sqrt{6} +\sqrt{2}\right)}{4}

我们还可以通过三角函数的变换公式求得18°时的值：

sin18°3=sin54°=sin（90°-36°）=cos36°=1-2sin18°^2

设sin18°=x 于是得到如下方程：

4x3+2x2−3x−1=04x^{3}+2x^{2}-3x-1=0

因式分解： （）（）（x+1）（4x2−2x−1）=0（x+1）（4x^{2}-2x-1）=0

解得x=sin18°= 5−14\frac{\sqrt{5}-1}{4}

但是以上似乎都只是幸运，剩下的三角函数值几乎都不能利用上述方法求出了。

例如sin10°或cos10°的值，你可以用三倍角公式来建立如下的方程：

sin30°=sin3∗10°=3sin10°−4sin10°3=12sin30°=sin3*10°=3sin10°-4sin10°^{3}=\frac{1}{2}

设sin10°=x 则我们得到了如下的三次方程：

x3−34x+18=0x^{3}-\frac{3}{4}x+\frac{1}{8}=0

先观察该三次方程的判别式：

Δ=(q2)2+(p3)3=(116)2+(−14)3=−3256<0\Delta=\left( \frac{q}{2} \right)^{2}+\left( \frac{p}{3} \right)^{3}=\left( \frac{1}{16} \right)^{2}+\left( -\frac{1}{4} \right)^{3}=-\frac{3}{256}<0

这表明该方程的有三个实数解，为了求出这三个解我们必须求出共轭虚根的表达式：

因为x= −q2+Δ3+−q2−Δ3=a+bi3+a−bi3\sqrt[3]{-\frac{q}{2}+\sqrt{\Delta}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\Delta}}=\sqrt[3]{a+bi}+\sqrt[3]{a-bi}

则本题中a= −q2-\frac{q}{2} = −116-\frac{1}{16} b= Δ=316\sqrt{\Delta}=\frac{\sqrt{3}}{16}

于是我们得到：

a+bi=−116+316ia+bi=-\frac{1}{16}+\frac{\sqrt{3}}{16}i = （）（）=18（−12+32i）=18（cos120°+isin120°）=\frac{1}{8}（-\frac{1}{2}+\frac{\sqrt{3}}{2}i）=\frac{1}{8}（cos120°+isin120°）

求出该复数的立方根：

x1= （）（）（）a+bi3=18（cos120+isin120°）3=12（cos120°3+isin120°3）=12（cos40°+isin40°）\sqrt[3]{a+bi}=\sqrt[3]{\frac{1}{8}（cos120+ i sin120°）}=\frac{1}{2}（cos\frac{120°}{3}+ isin\frac{120°}{3}）=\frac{1}{2}（cos40°+ isin40°）

根据虚根成对出现的原则，与之共轭的虚根为：

x2 （）=12（cos40°−isin40°）=\frac{1}{2}（cos40°- isin40°）

根据共轭虚根在复平面单位圆上均匀分布的原则，我们知道该方程的其他两对共轭虚根为：

x34 （（）（）（）=12（cos（40°+120°）±isin（40°+120°）=12（cos160°±isin160°）=\frac{1}{2}（cos（40°+120°）\pm isin（40°+120°）=\frac{1}{2}（cos160°\pm isin160°）

x56 （（）（）（）=12（cos（160°+120°）±isin（160°+120°）=12（cos280°±isin280°）=\frac{1}{2}（cos（160°+120°）\pm isin（160°+120°）=\frac{1}{2}（cos280°\pm isin280°）

具体分布情况如下图：

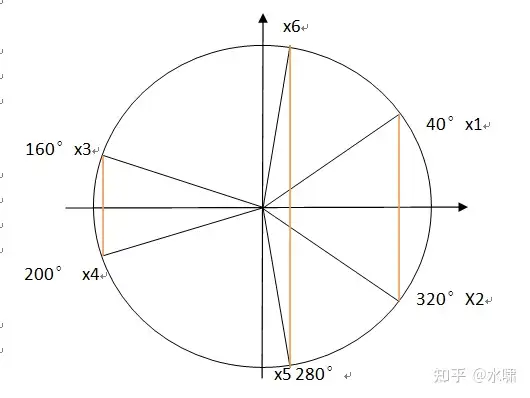
观察其中的第三对根x56：

（）（（）（）=12（cos280°±isin280°）=12（−cos（180°+100°）∓isin（180°+100°）=\frac{1}{2}（cos280°\pm isin280°）=\frac{1}{2}（-cos（180°+100°）\ \mp isin（180°+100°）

（）（）=12（−cos100°∓isin100°）=12（sin10°∓icos10°）=\frac{1}{2}（-cos100°\ \mp isin100°）=\frac{1}{2}（sin10°\ \mp icos10°）

这对虚根的实部正是我们所需要的解：

x实数解1= （（）（））2∗（12（sin10°+icos10°）+12（sin10°−icos10°））=sin10°2*（\frac{1}{2}（sin10°\ + icos10°）+\frac{1}{2}（sin10°\ -icos10°））=sin10°

这正是我们要求的方程 x3−34x+18=0x^{3}-\frac{3}{4}x+\frac{1}{8}=0 的解，可惜它不是一个数值，而是一个三角函数，这真是一个奇怪的现象，，，我们只能说，上帝认定我们已经会手工计算sin10°的值了。

但是仔细观察该方程，我们并没任何逻辑和计算上的错误，剩下的方法只能是用尝试法，也就是所谓的“手撕”法来求出sin10°的值了。

首先我们利用Excel表格作出该三次方程的大致的图像如下：

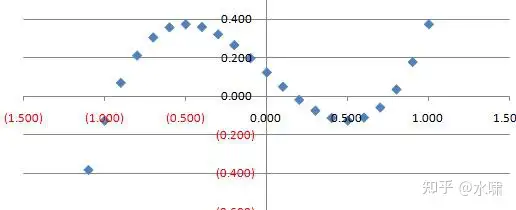
可以看到该方程有三个根，首先观察0附近的那个根，其大致范围如下：

也就是在0.1与0.2之间，缩小x的间距继续逼近得：

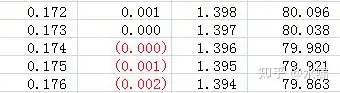
可见根的值应该在0.174~0.175之间，表格中的数据从左至右依次为x的值，函数的值，x值对应的弧度及角度值。

继续缩小x的变动范围得到如下结果：

x值在0.1736~0.1737之间，所对应的角度为80±0.003°。

查表得cos80°=0.17365=sin10°

可见这个根正是我要求的的sin10°的值，这这证明了该方程是没有问题的。同理该方程的另两个实根的值该分别是sin160°，sin40°的值，也就是sin20°和sin40°的值。

实际上数学天才拉马努金还曾经找到了一个表示cos10°的连根式如下：

cos10°=123(1+8−8−8+8−……)cos10°=\frac{1}{2\sqrt{3}}\left( 1+\sqrt{8-\sqrt{8-\sqrt{8+\sqrt{8-……}}}}\right)

用这个公式特点是收敛快可以迅速手撕，开七次方后即可精确到小数点后4位。

另一个方法是利用万能的泰勒级数展开式来求该值，已知正弦函数的展开式为：

sinx ！！！=x−x33！+x55！−x77！+……=x-\frac{x^{3}}{3！}+\frac{x^{5}}{5！}-\frac{x^{7}}{7！}+……

还行利用Excel表格我们计算到第3项时，把10°换算为弧度制的0.17453278代入上述就得到了sin10°=0.17364083而真值为0.173648

！！=0.17453278−0.1745327833！+0.1745327855！=0.17364083=0.17453278-\frac{0.17453278^{3}}{3！}+\frac{0.17453278^{5}}{5！}=0.17364083

并不像想象的收敛的那么慢。

结论是我们无法通过解三次方程的形式求得sin10°及cos10°的具体的实数值，而只能用近似法或级数展开法来求得。