圆锥曲线系列（八）【焦半径公式与焦点弦公式(2)】-圆锥曲线的焦半径公式推导

 

最近在重新学习圆锥曲线的过程中，感觉有很多东西非常有意思，我打算花费一些时间整理一下这部分的知识，如有错误、认识不足、缺漏，还请大家不吝赐教。这是本系列的第八篇，我们介绍焦半径与焦点弦的倾斜角形式的计算公式。这一篇与上一篇紧密相关，建议先看上一篇。

接下来我们直接给出倾斜角形式的焦半径公式与焦点弦公式：

【焦半径公式与焦点弦公式（倾斜角形式）】

（1）椭圆b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)中，设A,BA,B 为椭圆上的点（点A在x轴上方，点B在x轴下方），且直线ABAB 的倾斜角为 θ\theta ，设椭圆的离心率为 e=cae=\frac{c}{a} ，焦准距为 p=b2cp=\frac{b^{2}}{c}

，

(i) 如果直线 ABAB 过左焦点 F1F_1 ，那么 |AF1|=ep1−ecosθ|AF_1|=\frac{ep}{1-ecos\theta} ，|BF1|=ep1+ecosθ |BF_1|=\frac{ep}{1+ecosθ }

，

(ii) 如果直线 ABAB 过右焦点 F2F_2 ，那么 |AF2|=ep1+ecosθ|AF_2|=\frac{ep}{1+ecos\theta} ，|BF2|=ep1−ecosθ |BF_2|=\frac{ep}{1-ecosθ }

，

在这两种情况下，都有 1|AF|+1|BF|=2ep\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{ep} （弦AB经过焦点F），|AB|=2ep1−e2cos2θ|AB|=\frac{2ep}{1-e^{2}cos^{2}\theta}

；

（2）抛物线0)">y2=2px(p>0)y^2=2px(p>0)中，设A,BA,B 为椭圆上的点（点A在x轴上方，点B在x轴下方），且直线ABAB 的倾斜角为 θ\theta ，如果直线 ABAB 过焦点 FF ，那么 |AF|=p1−cosθ|AF|=\frac{p}{1-cos\theta} ，|BF|=p1+cosθ |BF|=\frac{p}{1+cosθ } ，且有 1|AF|+1|BF|=2p\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p} ，|AB|=2psin2θ|AB|=\frac{2p}{sin^{2}\theta}

；

（3）双曲线0)">x2a2−y2b2=1(a,b>0)\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)中，设A,BA,B 为椭圆上的点，且直线ABAB 的倾斜角为 θ\theta ，设椭圆的离心率为 e=cae=\frac{c}{a} ，焦准距为 p=b2cp=\frac{b^{2}}{c}

，

(i) 如果直线 ABAB 过左焦点 F1F_1，且 A,BA,B 都在左支上，点A在x轴上方，点B在x轴下方，那么 |AF1|=ep1+ecosθ|AF_1|=\frac{ep}{1+ecos\theta} ，|BF1|=ep1−ecosθ |BF_1|=\frac{ep}{1-ecosθ }

，

(ii) 如果直线 ABAB 过右焦点 F2F_2 ，且 A,BA,B 都在右支上，点A在x轴上方，点B在x轴下方，那么 |AF2|=ep1−ecosθ|AF_2|=\frac{ep}{1-ecos\theta} ，|BF2|=ep1+ecosθ |BF_2|=\frac{ep}{1+ecosθ }

，

上述两种情况，都有1|AF|+1|BF|=2ep\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{ep} （弦AB经过焦点F），|AB|=2ep1−e2cos2θ|AB|=\frac{2ep}{1-e^{2}cos^{2}\theta}

，

(iii) 如果直线 ABAB 过左焦点 F1F_1，且 AA 在左支上，BB 在右支上，那么 |AF1|=epe|cosθ|+1|AF_1|=\frac{ep}{e|cos\theta|+1} ，|BF1|=epe|cosθ|−1 |BF_1|=\frac{ep}{e|cos\theta|-1}

，

(iv) 如果直线 ABAB 过右焦点 F2F_2 ，且 AA 在左支上，BB在右支上，那么|AF1|=epe|cosθ|−1|AF_1|=\frac{ep}{e|cos\theta|-1}，|BF1|=epe|cosθ|+1 |BF_1|=\frac{ep}{e|cos\theta|+1}

，

上述两种情况，都有|AB|=2epe2cos2θ−1|AB|=\frac{2ep}{e^2cos^{2}\theta-1}

，

上述四种情况的焦点弦公式可以合并为|AB|=2ep|e2cos2θ−1||AB|=\frac{2ep}{|e^2cos^{2}\theta-1|}。

上述公式也是比较多，而且很相似，很容易记混淆了，另外还有椭圆b>0)">x2b2+y2a2=1(a>b>0)\frac{x^2}{b^2}+\frac{y^2}{a^2}=1(a>b>0)，抛物线0)">y2=−2px(p>0)y^2=-2px(p>0)，抛物线0)">x2=2py(p>0)x^2=2py(p>0)中抛物线0)">x2=−2py(p>0)x^2=-2py(p>0)，双曲线0)">y2a2−x2b2=1(a,b>0)\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a,b>0)中的焦半径公式和焦点弦公式我们还没有给出，所以还是要学会推导方法。

接下来我们以椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 为例来推导焦半径公式与焦点弦公式：

如图1，设 A,BA,B 在椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)上（点A在x轴上方，点B在x轴下方），且直线ABAB 的倾斜角为 θ\theta ，如果直线 ABAB 经过左焦点F1F_1，求 |AF1|,|BF1||AF_1|,|BF_1|

。

设左准线为 ll ，交x轴于点E，则 |EF1|=p|EF_1|=p ，过点 AA 作 AC⊥lAC\bot l ，则 |AF1||AC|=e\frac{|AF_1|}{|AC|}=e ，其中 |AC|=|EF1|+|AF1|cosθ=p+|AF1|cosθ|AC|=|EF_1|+|AF_1|cos\theta=p+|AF_1|cos\theta ，所以|AF1|p+|AF1|cosθ=e\frac{|AF_1|}{p+|AF_1|cos\theta}=e，解得 |AF1|=ep1−ecosθ|AF_1|=\frac{ep}{1-ecos\theta} ，同理|BF1|=ep1+ecosθ |BF_1|=\frac{ep}{1+ecosθ } ，所以1|AF1|+1|BF1|=2ep\frac{1}{|AF_1|}+\frac{1}{|BF_1|}=\frac{2}{ep} ，|AB|=|AF1|+|BF1|=2ep1−e2cos2θ|AB|=|AF_1|+|BF_1|=\frac{2ep}{1-e^{2}cos^{2}\theta}。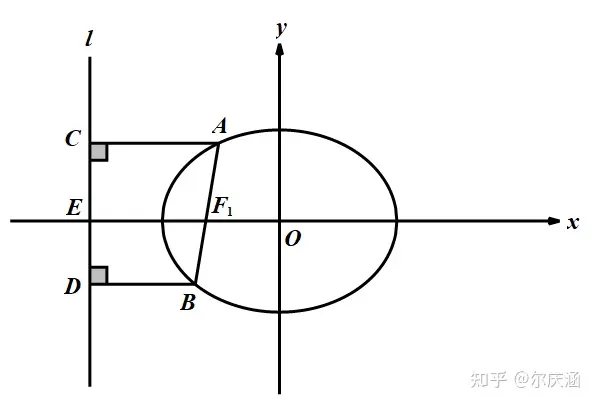 图1

老规矩，为了学以致用，接下来还是看一个例题：

【例题】（2022上海交通大学强基）点 F1,F2F_1,F_2 为双曲线的两个焦点（焦点在 xx 轴上），直线 ABAB 经过 F1F_1 ，且与双曲线左右两支分别交于点 AA 、 BB ， 2|AF1|=|AB|2|AF_{1}|=|AB| ， ∠F1AF2=120°\angle F_1AF_2=120° ，求双曲线的离心率．

【解析】设直线ABAB与x轴的夹角为 θ\theta ，那么 |AF1|=epecosθ+1|AF_{1}|=\frac{ep}{ecos\theta+1} ，|BF1|=epecosθ−1|BF_{1}|=\frac{ep}{ecos\theta-1} ，又因为 |BF1|=|AF1|+|AB|=3|AF1||BF_{1}|=|AF_{1}|+|AB|=3|AF_{1}| ，所以 epecosθ−1=3epecosθ+1\frac{ep}{ecos\theta-1}=\frac{3ep}{ecos\theta+1} ，解得 ecosθ=2ecos\theta=2 ，所以|AF1|=ep3=b23a=c2−a23a|AF_{1}|=\frac{ep}{3}=\frac{b^2}{3a}=\frac{c^2-a^2}{3a}，所以|AF2|=|AF1|+2a=c2−a23a+2a=c2+5a23a|AF_{2}|=|AF_{1}|+2a=\frac{c^2-a^2}{3a}+2a=\frac{c^2+5a^2}{3a}，又 |F1F2|=2c|F_1F_2|=2c ，根据余弦定理，有 cos∠F1AF2=|AF1|2+|AF2|2−|F1F2|22|AF1||AF2|=cos120°=−12cos\angle F_1AF_2=\frac{|AF_{1}|^2+|AF_{2}|^2-|F_1F_2|^2}{2|AF_{1}||AF_{2}|}=cos120°=-\frac{1}{2} ，所以 (c2−a2)2+(c2+5a2)2−36a2c22(c2−a2)(c2+5a2)=−12\frac{(c^2-a^2)^2+(c^2+5a^2)^2-36a^2c^2}{2(c^2-a^2)(c^2+5a^2)}=-\frac{1}{2} ，所以 (e2−1)2+(e2+5)2−36e22(e2−1)(e2+5)=−12\frac{(e^2-1)^2+(e^2+5)^2-36e^2}{2(e^2-1)(e^2+5)}=-\frac{1}{2} ，解得e2=7e^2=7，所以 e=7e=\sqrt{7} 。

图2

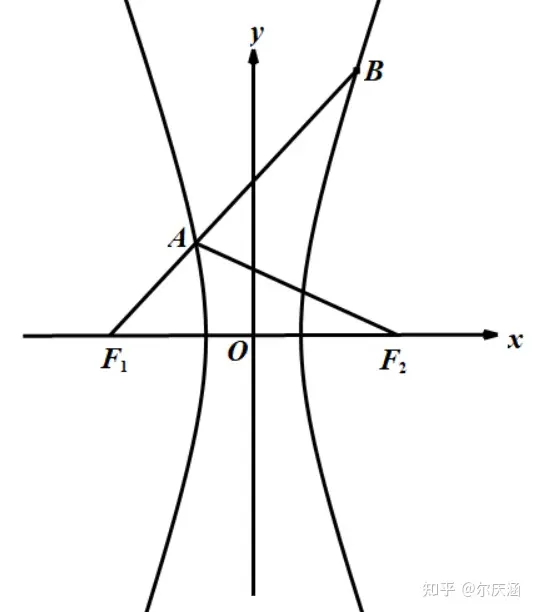
另外，上一讲的例题也可以使用这个方法来计算，而且这个方法会更加快捷，有兴趣的朋友可以试试看。

以上就是圆锥曲线系列的第八篇——焦半径公式与焦点弦公式(2)。注意本文提到的公式千万不能滥用，一定要直线过焦点才能用！！！另外本文中的公式在高考中可以直接用，不必先证后用。