高中数学：集合（高中数学集合知识点全总结）

2023-06-01 04:17:28

集合的概念与表示

现代数学中，最基础的东西不是数，也不是图形，而是集合与逻辑。数字、图形都可以用集合与逻辑来定义（不过这种定义不在高中数学的范围内）。由此可见集合与逻辑的重要性。

集合很容易理解。顾名思义，集合就是一些东西。可以把集合理解为一个盒子，它里面可以有各种各样的东西，可以有无穷多个东西，也可以什么都没有。我们把集合里面的东西叫做这个集合的元素。如果一个元素 $a$ a 在一个集合 $A$ A 中，我们说“ $a$ a 属于 $A$ A"，用符号记作 $a\inA$ a\in A。例如，这是一个集合，它的元素是 $2$ 2、 $3$ \sqrt{3}、 $π$ \pi：

没有东西也是一个集合，这个集合叫做”空集“，记作 $\emptyset$ \varnothing：

有一些常见的集合有特殊的名字。以所有非负整数（自然数）为元素的集合叫做 $N$ \mathbb{N}；以所有正整数为元素的集合叫做 $N*$ \mathbb{N}^* 或 $N+$ \mathbb{N}_+；以所有整数为元素的集合叫做 $Z$ \mathbb{Z}；以所有有理数为元素的集合叫做 $Q$ \mathbb{Q}；以所有实数为元素的集合叫做 $R$ \mathbb{R}。

数学中的集合还有一些性质。这两个集合 $A$ A、 $B$ B 的元素完全一样， $A$ A 的元素都属于 $B$ B， $B$ B 的元素都属于 $A$ A，只是我们画的顺序不一样。这种情况下，我们认为 $A$ A 和 $B$ B 是相同的：

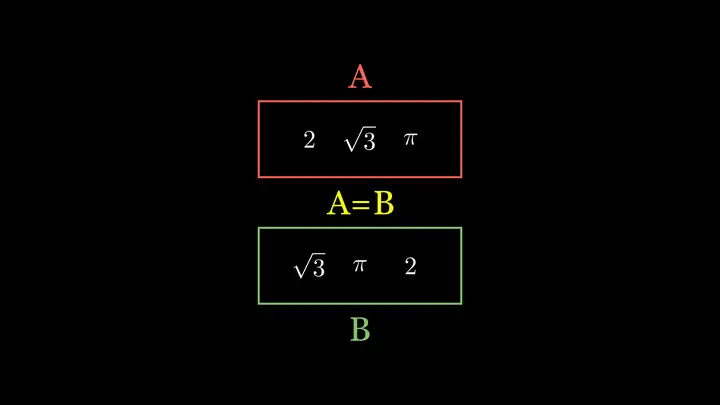
集合中，同一个元素不能重复出现多次。例如，这不是一个集合：

到目前为止，我们通过画画来表示一个集合。但数学家们觉得这样表示太麻烦了，就创造了一种集合的表示方式，叫做列举法。它本质上和画画没有区别。例如，我们刚才画出的第一个集合用列举法表示为 ${2,3,π}$ \{ 2,\sqrt{3},\pi \}。

用列举法能表示很多集合。我们画画能画出来的，列举法都能表示出来。但列举法不能表示所有集合。例如一个以所有正实数为元素的集合，列举法就无法表示。不可能把所有正实数一个个列举出来，因为正实数有无穷多个。那么怎么办呢？

我们说“以所有正实数为元素的集合”这句话，就已经表示出了一个集合，只不过是用中文表示的，而不是用严谨的数学语言表示的。如果我们把这句话翻译成数学语言，就得到集合的另一种表示方法：描述法。我们要翻译”以所有正实数为元素的集合“，首先给这个集合的元素取一个名字，这里叫 $x$ x。然后， $x$ x 为实数，也就是 $x\inR$ x\in \mathbb{R}。最后， $x$ x 为正数，也就是 0"> $x>0$ x>0。再加上一些符号，得到”以所有正实数为元素的集合“用描述法表示为 0\}"> ${x|x\inR,x>0}$ \{x|x\in \mathbb{R},x>0\}。两边的大括号代表这是一个集合，竖线左边是我们为集合中的元素取的名字，右边是这个元素需要满足的条件。

为了方便，有时把条件 $x\inR$ x\in \mathbb{R} 写在竖线左边，所以 0\}"> ${x|x\inR,x>0}$ \{x|x\in \mathbb{R},x>0\} 有时简化为 0\}"> ${x\inR|x>0}$ \{x\in \mathbb{R}|x>0\}。除此以外，高中数学中，经常把 $x\inR$ x\in \mathbb{R} 省略，如果没有专门说，就默认 $x\inR$ x\in \mathbb{R}。所以 0\}"> ${x\inR|x>0}$ \{x\in \mathbb{R} | x>0\} 经常再简化为为 0\}"> ${x|x>0}$ \{x | x>0\}。（但如果我们要的不是所有正实数，而是所有正有理数，那还是要写 0\}"> ${x\inQ|x>0}$ \{x\in \mathbb{Q} | x>0\}。）

我们再试试用描述法表示另一个集合：以所有平方数为元素的集合。我们还是设这个集合的元素为 $x$ x。关键就在于如何翻译” $x$ x 为平方数“。” $x$ x 为平方数“的意思就是“有一个整数的平方为 $x$ x“。这样，我们就能得出这个集合用描述法的表示了： ${x|x=n2,n\inZ}$ \{x|x=n^2,n\in \mathbb{Z}\}。这个表示有时简化为 ${n2|n\inZ}$ \{n^2|n\in \mathbb{Z}\}，把 $x=n2$ x=n^2 省略，直接把集合中的元素叫做 $n2$ n^2。

再看一看这个集合： ${x\inN|y=1x}$ \{x\in \mathbb{N}|y=\frac{1}{x}\}。看起来，竖线右边的条件” $y=1x$ y=\frac{1}{x}“似乎没有传达任何信息，因为给出一个 $x$ x，必然存在一个 $y=1x$ y=\frac{1}{x}。但要注意，表达式 $1x$ \frac{1}{x} 必须要有定义，这样才存在 $y=1x$ y=\frac{1}{x}。所以集合 ${x\inN|y=1x}$ \{x\in \mathbb{N}|y=\frac{1}{x}\} 就是非零的非负整数，也就是正整数（ $N*$ \mathbb{N}^*）。所以，在竖线右边的条件中，要注意表达式是否有定义。

最后，要注意不是所有看起来像描述法的表示都能表示一个集合，给出的条件必须有准确的定义。例如， $很大 {x|x很大}$ \{x|x很大\} 不能表示一个集合，因为给出一个 $x$ x，我们不能准确地判断 $x$ x 是否很大， $x$ x 很大这个条件没有准确的定义。

因为像 $\{x|-2<span class=$ \{x|a\le x<b\} 记作 $[a,b)$ [a,b)。总之，如果区间的一端含等号，这一端就用”[“；如果不含等号，就用”(“。还有一些区间，只有一个端点，像 ${x|x\leq1}$ \{x|x\le 1\}。对于这些区间，我们把它的另一个端点规定为正无穷大或负无穷大，且用”(“（因为区间不包括正负无穷大本身）。这样， ${x|x\leq1}$ \{x|x\le 1\} 可以记作 $(-\infty,1]$ (-\infty,1]。同理，4\}"> ${x|x>4}$ \{x|x>4\} 可以记作 $(4,+\infty)$ (4,+\infty)。

集合的关系与运算

如果有两个集合 $A$ A、 $B$ B，且 $A$ A 的元素都属于 $B$ B，那么我们说” $A$ A 是 $B$ B 的子集“，或” $A$ A 包含于 $B$ B“，记作 $A\subseteqB$ A\subseteq B。例如，集合 $东西 {东,西}$ \{东,西\} 包含于集合 $东西南北 {东,西,南,北}$ \{东,西,南,北\}。注意包含于和属于的差异。 $A$ A 属于 $B$ B 意思是” $A$ A 是 $B$ B 的元素“，而不是” $A$ A 的元素都是 $B$ B 的元素“。

空集包含于任何集合，因为空集没有元素，它的所有元素都属于任何一个集合。

根据上述的定义，任何集合包含于它自己，因为它自己的元素都属于它自己。如果 $A\subseteqB$ A\subseteq B，且 $A\neqB$ A\neq B，那么我们说” $A$ A 是 $B$ B 的真子集“，记作 $A⊊B$ A\subsetneq B。例如， $张三李四 \emptyset⊊{张三,李四}$ \varnothing \subsetneq \{张三,李四\}， $张三张三李四 {张三}⊊{张三,李四}$ \{张三\} \subsetneq \{张三,李四\}，但 $张三李四张三李四 {张三,李四}⊊{张三,李四}$ \{张三,李四\} \subsetneq \{张三,李四\} 不成立。

若一个集合有 $n$ n 个元素，它的子集个数为 $2n$ 2^n。这可以这样理解：如果我们要选出一个子集，我们要判断第一个元素是否要属于子集，再判断第二个元素是否要属于子集，等等，直到判断第 $n$ n 个元素是否要属于子集。总共要做 $n$ n 次判断，每次判断的结果有两种可能，所以共有 $2n$ 2^n 组不同的判断；每一组判断对应一个子集，每一个子集对应一组判断，所以子集个数也为 $2n$ 2^n。

如果有两个集合 $A$ A、 $B$ B，那么定义集合 $A\cupB$ A\cup B（读作” $A$ A 与 $B$ B 的并集“，简称” $A$ A 并 $B$ B“）为 $或 {x|x\inA或x\inB}$ \{x|x\in A 或 x\in B\}。意思就是说，如果一个元素属于 $A$ A，或者属于 $B$ B，那么它就属于 $A\cupB$ A\cup B。要注意，如果一个元素属于 $A$ A，也属于 $B$ B，它在 $A\cupB$ A\cup B 中也只出现一次，因为集合中不能出现重复的元素。例如， $(-1.+\infty)\cup(-\infty,1]=R$ (-1.+\infty)\cup (-\infty,1]=\mathbb{R}。

类似，如果有两个集合 $A$ A、 $B$ B，那么定义集合 $A\capB$ A\cap B（读作” $A$ A 与 $B$ B 的交集“，简称” $A$ A 交 $B$ B“）为 $且 {x|x\inA且x\inB}$ \{x|x\in A 且 x\in B\}。意思就是说，如果一个元素既属于 $A$ A，也属于 $B$ B，那么它就属于 $A\capB$ A\cap B。例如， $(-1.+\infty)\cap(-\infty,1]=(-1,1]$ (-1.+\infty)\cap (-\infty,1]=(-1,1]。

最后，如果有一个集合 $U$ U，集合 $A\subseteqU$ A\subseteq U，那么定义集合 $∁UA$ \complement_UA（读作“ $A$ A 关于 $U$ U 的补集，在上下文明确时，可以简称“ $A$ A 的补集”）为 ${x\inU|x\notinA}$ \{x\in U|x\notin A\}（ $\notin$ \notin 指不属于）。意思就是说，在集合 $U$ U 中，那些不在 $A$ A 中的元素就属于 $∁UA$ \complement_UA。例如，如果 $A=[-1,1]$ A=[-1,1]，则 $∁RA=(-\infty,-1)\cup(1,+\infty)$ \complement_{\mathbb{R}}A=(-\infty,-1)\cup (1,+\infty)。

求区间的并、交、补集运算时，应特别注意区间两端应打"("")"还是"[""]"，并根据并、交、补集的定义来判断。例如， $∁R(2,5]=(-\infty,2]\cup(5,+\infty)$ \complement_R(2,5]=(-\infty,2]\cup (5,+\infty)，因为 $2\notin(2,5]$ 2\notin (2,5]， $5\in(2,5]$ 5\in (2,5]，所以 $2\in∁R(2,5]$ 2\in \complement_R (2,5]， $5\notin∁R(2,5]$ 5\notin \complement_R (2,5]。

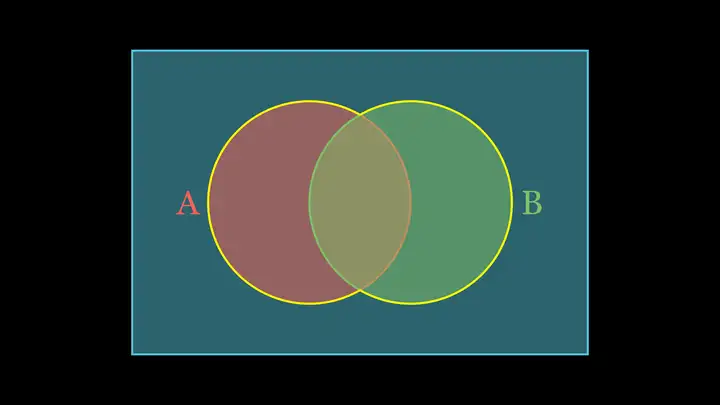
我们可以通过画图，我们可以清晰地看出集合之间的关系以及集合的运算。这种图叫做Venn图。例如这里，红线以内的区域代表集合 $A$ A，绿线以内区域代表集合 $B$ B，蓝线以内的区域代表集合 $U$ U。这样一来，可见黄线以内区域就是 $A$ A 或 $B$ B 中的区域，所以黄线内区域代表集合 $A\cupB$ A\cup B。类似，棕色区域代表集合 $A\capB$ A\cap B，蓝色区域代表集合 $∁U(A\cupB)$ \complement_U(A\cup B)。从Venn图可以看出不少集合的性质，例如 $∁A(A\capB)=∁A\cupBB$ \complement_A (A\cap B)=\complement_{A\cup B}B（因为 $∁A(A\capB)$ \complement_A (A\cap B) 和 $∁A\cupBB$ \complement_{A\cup B}B 都是图中的红色区域），以及若 $A\subseteqU$ A\subseteq U，则 $U\capA=A$ U\cap A=A、 $U\cupA=U$ U\cup A=U 等（具体细节请读者自行补充）。

已知集合的运算

高考中，对集合的考察以考察集合的表示与已知的集合的并集、交集、补集的求法为主。

如果要求用列举法表示的集合的并、交、补，就根据并、交、补的定义，列举出并集、交集、补集中的元素。（像这种黑体字，有不少都是解题方法，看完应该对照下面的例题，观察例题是如何使用这个解题方法的。）

例1.（2020全国II卷理）已知集合 $U={-2,-1,0,1,2,3}$ U=\{-2,-1,0,1,2,3\}， $A={-1,0,1}$ A=\{-1,0,1\}， $B={1,2}$ B=\{1,2\}，则 $∁U(A\cupB)=$ \complement _U (A\cup B)=A. ${-2,3}$ \{-2,3\} B. ${-2,2,3}$ \{-2,2,3\} C. ${-2,-1,0,3}$ \{-2,-1,0,3\} D. ${-2,-1,0,2,3}$ \{-2,-1,0,2,3\}

这道题中，因为 $U$ U、 $A$ A、 $B$ B 都是确定的集合，所有我们直接根据并、补集的定义来求 $∁U(A\cupB)$ \complement _U (A\cup B)。先求 $A\cupB$ A\cup B。那些在 $A$ A 中，或者在 $B$ B 中的元素为 $-1$ -1、 $0$ 0、 $1$ 1、 $2$ 2，所以 $A\cupB={-1,0,1,2}$ A\cup B=\{-1,0,1,2\}。然后求它关于 $U$ U 的补集。那些在 $U$ U 中，但不在 $A\cupB$ A\cup B 中的元素为 $-2$ -2、 $3$ 3，所以 $∁U(A\cupB)={-2,3}$ \complement _U (A\cup B)=\{-2,3\}。故本题选A。

如果要求用描述法表示的集合的并、交、补，就结合集合中元素需要满足的条件求解。 $A\cupB$ A\cup B 中的元素满足 $A$ A 的条件或 $B$ B 的条件； $A\capB$ A\cap B 中的元素同时满足 $A$ A 的条件和 $B$ B 的条件； $∁UA$ \complement_U A 中的元素满足 $U$ U 的条件，但不满足 $A$ A 的条件。如果不好直接看出答案，可以在数轴上标出两个集合，由此得出答案。

例2.（2019全国II卷理）设集合 0\}"> $A={x|x2-5x+6>0}$ A=\{x|x^2-5x+6>0\}， $B=\{x|x-1<span class=$ B=\{x|x-1<0\}，则 $A\capB=$ A\cap B=A. $(-\infty,1)$ (-\infty,1) B. $(-2,1)$ (-2,1) C. $(-3,-1)$ (-3,-1) D. $(3,+\infty)$ (3,+\infty)

这里， $A$ A、 $B$ B 都是确定的集合，所以直接根据交集的定义来求 $A\capB$ A\cap B。我们联立 $A$ A、 $B$ B 中元素需要满足的条件：

$ x2-5x+6>0 x-1<0 $ \begin{align*} x^2-5x+6&>0\\ x-1&<0\\ \end{align*}

解得 $x<span class=$ x<1，所以 $A\capB=(-\infty,1)$ A\cap B=(-\infty,1)。故本题选A。

如果不好直接看出答案，可以在数轴上标出两个不等式的解集：

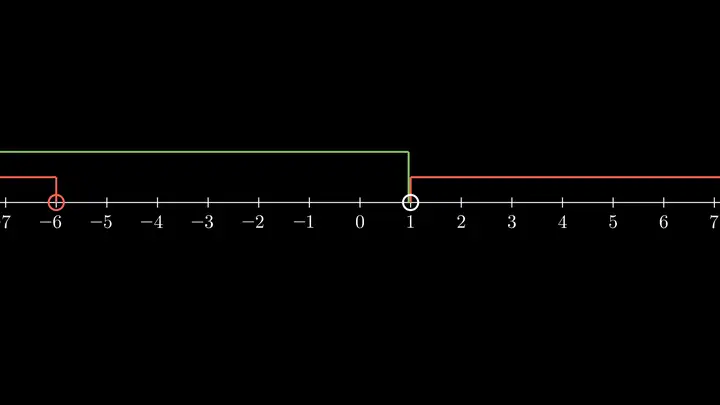
如果集合的含义不清晰，先应该搞清楚这个集合的含义。可以通过代入特殊值来搞清楚集合的含义。

例3.（2021全国乙卷理）已知集合 $S={s|s=2n+1,n\inZ}$ S=\{s|s=2n+1,n\in \mathbb{Z}\}， $T={t|t=4n+1,n\inZ}$ T=\{t|t=4n+1,n\in \mathbb{Z}\}，则 $S\capT=$ S\cap T=A. $\emptyset$ \varnothing B. $S$ S C. $T$ T D. $Z$ \mathbb{Z}

这里， $S$ S、 $T$ T 仍然是确定的集合，但它们的描述没有前面两道题那么清晰。所以，我们先搞清楚 $S$ S、 $T$ T 是什么样子的集合。 $S$ S 的元素是那些能表示为 $2n+1$ 2n+1 形式的数，其中 $n$ n 为整数。如果一眼看不出来，可以代入一些 $n$ n 值，比如代入 $n=-1,0,1$ n=-1,0,1，然后就能发现 $S$ S 的元素是所有奇数： ${...,-3,-1,1,3,5,...}$ \{...,-3,-1,1,3,5,...\}。同理，可以发现 $T$ T 的元素是所有除以 $4$ 4 的余数为 $1$ 1 的数： ${...,-3,1,5,9,...}$ \{...,-3,1,5,9,...\}。

然后再来求 $S\capT$ S\cap T，也就是求那些既在 $S$ S 中，也在 $T$ T 中的元素。容易看出， $T⊊S$ T\subsetneq S， $T$ T 的元素都是 $S$ S 的元素，所以 $S\capT=T$ S\cap T=T。故本题选C。（我们上面用Venn图得到了这个结论：若 $A\subseteqU$ A\subseteq U，则 $U\capA=A$ U\cap A=A、 $U\cupA=U$ U\cup A=U。）

有关集合的关系式的求解

高考中，偶尔会给出含参数的集合，再给出有关集合的关系式，然后需要由此求出参数。对于这一类问题，必须要回到并、交、补、属于、包含于的定义，再考虑一个集合确定时，另一个集合需要满足什么条件，有必要时借助Venn图，由此把集合的关系式化为更容易处理的关系。然后，把每个集合用参数以最简单的形式表示出来（尽量用列举法或区间表示），最终列出有关参数的关系式。此外，如果用Venn图，看见 $A\subseteqB$ A\subseteq B，应特别注意 $A=B$ A=B 的情况，因为此时Venn图会有变化。

例1. 已知全集 $U$ U，集合 $P$ P， $S$ S 是 $U$ U 的非空子集，且 $S\subseteq∁UP$ S\subseteq \complement_U P

，则必有

P\subseteq∁US

P\subseteq \complement_U S B.

P\subseteqS

P\subseteq S C.

∁UP=∁US

\complement_U P=\complement_U S D.

P\cap(∁US)=\emptyset

P\cap (\complement_U S)=\varnothing

看见复杂集合关系，我们就画出Venn图。先画出 $U$ U 和 $P$ P：

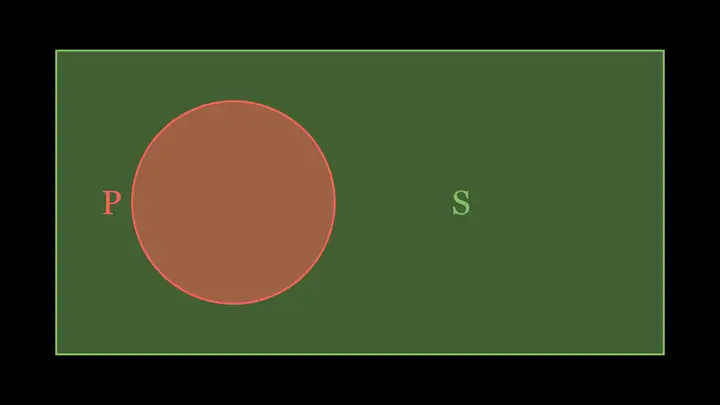
上图中绿色区域就是 $∁UP$ \complement_U P，而 $S\subseteq∁UP$ S\subseteq \complement_U P，所以这是 $U$ U、 $P$ P、 $S$ S：

这样就能看出，选项A正确，B、C、D错误。（具体细节请读者自行补充）但还要再注意 $S=∁UP$ S=\complement_U P 时是什么情况，因为此时Venn图会有变化。此时易知Venn图如图所示，红色区域为 $P$ P，绿色区域为 $S$ S，可见此时A仍然成立。

例2.（2013上海卷）设常数 $a\inR$ a\in \mathbb{R}，集合 $A={x|(x-1)(x-a)\geq0}$ A=\{x|(x-1)(x-a)\ge 0\}， $B={x|x\geqa-1}$ B=\{x|x\ge a-1\}，若 $A\cupB=R$ A\cup B=\mathbb{R}，则 $a$ a

的取值范围为

(-\infty,2)

(-\infty,2) B.

(-\infty,2]

(-\infty,2] C.

(2,+\infty)

(2,+\infty) D.

[2,+\infty)

[2,+\infty)

我们考虑哪些 $B$ B 能使得 $A\cupB=R$ A\cup B=\mathbb{R}。为了使 $A\cupB=R$ A\cup B=\mathbb{R}，需要属于 $R$ \mathbb{R} 的每一个元素都属于 $A$ A 或者属于 $B$ B，也就需要那些不属于 $A$ A 的元素都属于 $B$ B，也就是需要 $∁RA\subseteqB$ \complement_\mathbb{R}A\subseteq B。（这里我们没有用Venn图，不用检验 $∁RA=B$ \complement_\mathbb{R}A=B 的情况）

而 $\complement_\mathbb{R}A=\{x|(x-1)(x-a)<span class=$ a<1，则 $∁RA=(a,1)$ \complement_\mathbb{R}A=(a,1)，又 $B={x|x\geqa-1}$ B=\{x|x\ge a-1\}，所以 $∁RA\subseteqB$ \complement_\mathbb{R}A\subseteq B 恒成立；若 $a=1$ a=1，则 $∁RA=\emptyset\subseteqB$ \complement_\mathbb{R}A=\varnothing \subseteq B；若 1"> $a>1$ a>1，则 $∁RA=(1,a)$ \complement_\mathbb{R}A=(1,a)，此时若 $∁RA\subseteqB$ \complement_\mathbb{R}A\subseteq B，需要 $a\geq2$ a\ge 2。综上所述， $a$ a 的取值范围为 $(-\infty,2]$ (-\infty,2]。（如果不确定右边应该是小括号还是中括号，就代入 $a=2$ a=2，看看是否有 $∁RA\subseteqB$ \complement_\mathbb{R}A\subseteq B。）

对于一些较为复杂的集合关系式，应该像下一道题这样，分步画Venn图，不需要一次性确定所有集合。

例3. 已知集合 $A=\{x|1<x<span class=$ A=\{x|1<x<2\}，集合 $B={x|x\geqm}$ B=\{x|x\ge m\}，若 $A\cap(∁RB)=\emptyset$ A\cap (\complement_{\mathbb{R}} B)=\varnothing，则 $m$ m

的取值范围为

(-\infty,1]

(-\infty,1] B.

(-\infty,2]

(-\infty,2] C.

[1,+\infty)

[1,+\infty) D.

[2,+\infty)

[2,+\infty)

我们画出Venn图。先画出 $R$ \mathbb{R} 和 $A$ A：

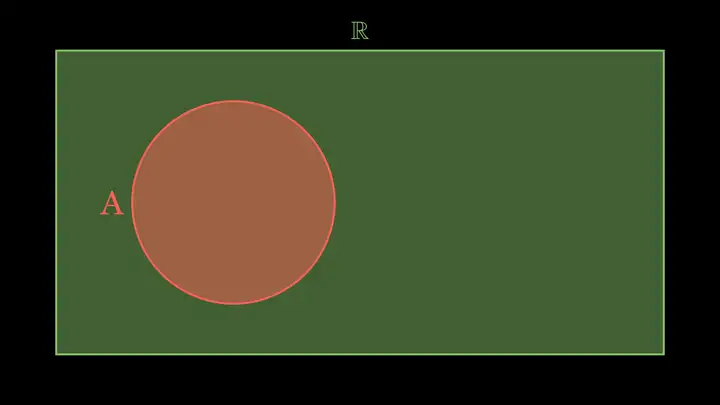
然后，我们考虑哪些 $B$ B 能使得 $A\cap(∁RB)=\emptyset$ A\cap (\complement_{\mathbb{R}} B)=\varnothing。我们不需要直接画出 $B$ B，而是先画出 $∁RB$ \complement_{\mathbb{R}} B，因为这一个条件的意思是 $A$ A 和 $∁RB$ \complement_{\mathbb{R}} B 没有重合，如图所示：

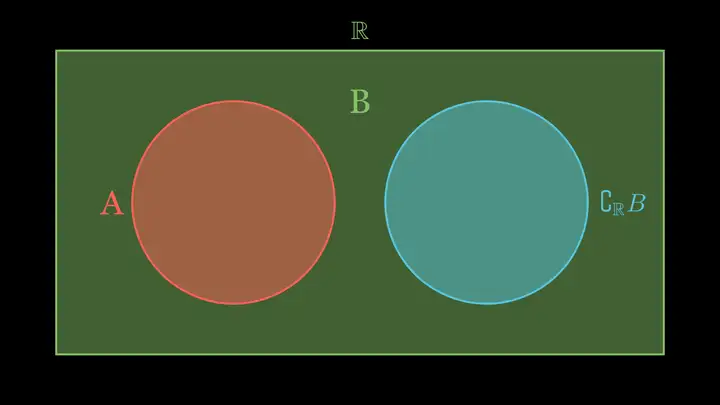
而 $∁RB$ \complement_{\mathbb{R}} B 就是那些属于 $R$ \mathbb{R} 但不属于 $B$ B 的元素，所以可见 $B$ B 就是图中的绿色区域。由此可见， $A\subseteqB$ A\subseteq B。此时应该特别注意 $A=B$ A=B 的情况。容易发现 $A=B$ A=B 时仍然有 $A\cap(∁RB)=\emptyset$ A\cap (\complement_{\mathbb{R}} B)=\varnothing。所以，我们把 $A\cap(∁RB)=\emptyset$ A\cap (\complement_{\mathbb{R}} B)=\varnothing 等价转化为了 $A\subseteqB$ A\subseteq B。

我们已知 $A=\{x|1<x<span class=$ A=\{x|1<x<2\}， $B={x|x\geqm}$ B=\{x|x\ge m\}，所以显然 $A\subseteqB$ A\subseteq B 时， $m$ m 的取值范围为 $(-\infty,1]$ (-\infty,1]。

如果集合是用列举法表示的，在按照上面的方法做完后，要根据集合之间的关系来分类讨论。要注意集合内的元素不能相同。

例4. 已知集合 $A={1,3,a2}$ A=\{1,3,a^2\}， $B={1,a+2}$ B=\{1,a+2\}，若 $A\capB=B$ A\cap B=B，则实数 $a$ a

的值为

1

1 B.

-1

-1 或

2

2 C.

2

2 D.

-1

-1 或

1

给定 $A$ A，我们考虑哪些 $B$ B 能使得 $A\capB=B$ A\cap B=B。 $A\capB=B$ A\cap B=B 的意思就是那些既属于 $A$ A，也属于 $B$ B 的元素就是 $B$ B 的所有元素，也就是 $B$ B 的所有元素都也属于 $A$ A，也就是 $B\subseteqA$ B\subseteq A。所以我们来观察 $A$ A、 $B$ B 的元素。我们发现， $B$ B 的元素 $1$ 1 也属于 $A$ A，所以需要 $a+2\inA$ a+2\in A。

我们得出了 a+2 是 A 的元素，但我们不知道 a+2 是 A 的哪个元素，所以我们分类讨论。若 a+2=1，则 a=-1。若 a+2=3，则 a=1。若 a+2=a^2，则 a=-1 或 2。综上所述，我们得到 a 为 -1 或 1 或 2。

但我们还要检验集合内元素是否相同。若 a=-1，A=\{1,3,1\}，元素有重复，这是不行的。若 a=1，也有 A=\{1,3,1\}，元素有重复，也是不行的。若 a=2，则 A=\{1,3,4\}，B=\{1,3\}，没有重复。故答案为 a=2。

集合新定义问题

集合题目可以出得很难。这一类难题一般会要求探究满足某些性质的集合，或者某种新的运算等，题目五花八门，所幸全国除北京外，高考很少考这一类题目。这一类题目，我们这里统称“集合新定义问题”。

对于集合新定义问题，最好的办法就是探索。探索时，应该从简单的情况开始，然后再借鉴处理简单的情况的方法，去处理复杂的情况；从特殊的情况开始，然后再参考探索特殊的情况归纳出的结论，去处理一般的情况。探索的过程中要注意充分利用已知条件。

例1.（2020浙江卷）设集合 S、T，S\subseteq N^*，T\subseteq N^*，S、T 中都至少有两个元素，且 S、T 满足：（1）对于任意 x,y\in S，若 x\neq y，都有 xy\in T；（2）对于任意 x,y\in T，若 b>a=1，所以 c>b，所以 1=a">\frac{c}{b}>1=a，所以必然 \frac{c}{b}=b，即 c=b^2。这样一来，S=\{1,b,b^2\}，因为 ab,ac,bc\in T，所以 \{b,b^2,b^3\}\subseteq T。容易发现，T 中不可能还有其它元素，否则就不能满足条件（2）（具体细节请读者自行补充），所以 T=\{b,b^2,b^3\}，S\cup T=\{1,b,b^2,b^3\}，有四个元素。

若 1">a>1，\frac{b}{a}=a，所以 b=a^2。用 \frac{b}{a} 得不出更多的信息了，所以接下来，我们换一个，分析 \frac{c}{a}。我们知道，\frac{b}{a}=a">\frac{c}{a}>\frac{b}{a}=a，a>1 的情况。

若 a=1，\frac{b}{a}=b，\frac{c}{a}=c，\frac{d}{a}=d，\frac{d}{b}>\frac{c}{b}=b，a>1，有 \frac{b}{a}=a，所以 b=a^2。因为 \frac{b}{a}=a">\frac{c}{a}>\frac{b}{a}=a，\frac{d}{a}>\frac{c}{a}=b，本文使用 Zhihu On VSCode 创作并发布

以上就是关于《高中数学：集合（高中数学集合知识点全总结）》的全部内容，本文网址：https://www.7ca.cn/baike/41848.shtml，如对您有帮助可以分享给好友，谢谢。

标签:

声明