手撕CFD求解器之QUICK格式(1)-手撕hard

QUICK格式全称Quadratic Upwind Interpolation of the Convective Kinematics，即对流项的二次迎风插值。为什么要提出QUICK格式呢？因为之前的FUD和HS都只具有一阶截差，不够精确，容易数值扩散。QUICK格式提出就是为了提高精度，同时还想保持迎风的性质。

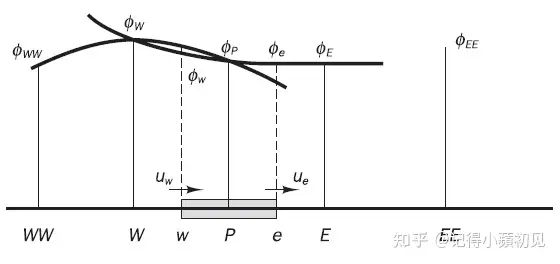
QUICK格式是一种五点格式，一个控制体会牵涉到五个点：WW、W、P、E、EE。在确定某个面上的界面函数时，要用到面左右的两个点和其上游的一个点。

这次先讲QUICK种内节点的离散。

理论部分

QUICK格式是二次插值，比如 ww 面，要用WW、W、P三个点确定一个二次函数曲线，然后把曲线上 ww 面处的值作为 ϕw\phi_w。确定 ϕw\phi_w的方法有很多，初中方法就能做，不过这里最快最简便的方法是用拉格朗日插值。任给三个点 (x1,y1)(x_1,y_1)，(x2,y2)(x_2,y_2)，(x3,y3)(x_3,y_3)，可确定一条二次曲线 P2(x)P_2(x)：

P2(x)=y1(x−x2)(x−x3)(x1−x2)(x1−x3)+y2(x−x1)(x−x3)(x2−x1)(x2−x3)+y3(x−x1)(x−x2)(x3−x1)(x3−x2)P_2(x)=y_1 \frac{\left(x-x_2\right)\left(x-x_3\right)}{\left(x_1-x_2\right)\left(x_1-x_3\right)}+y_2 \frac{\left(x-x_1\right)\left(x-x_3\right)}{\left(x_2-x_1\right)\left(x_2-x_3\right)}+y_3 \frac{\left(x-x_1\right)\left(x-x_2\right)}{\left(x_3-x_1\right)\left(x_3-x_2\right)} \\

在我们的情境中，假定P的横坐标为0，则三个点的坐标是 P(0,ϕP)P(0,\phi_P)，W(−Δx,ϕW)W(-\Delta x,\phi_W)，WW(−2Δx,ϕWW)WW(-2\Delta x,\phi_{WW})，界面 ww 位于 w(−Δx/2,ϕw)w(-\Delta x/2,\phi_w)，代入插值公式：

ϕw=ϕP(Δx/2)(3Δx/2)(Δx)(2Δx)+ϕW(−Δx/2)(3Δx/2)(−Δx)(Δx)+ϕWW(−Δx/2)(Δx/2)(−2Δx)(−Δx)=3ϕP+6ϕW−ϕWW8\begin{align} \phi_w&=\phi_P\frac{(\Delta x/2)(3\Delta x/2)}{(\Delta x)(2\Delta x)}+\phi_W\frac{(-\Delta x/2)(3\Delta x/2)}{(-\Delta x)(\Delta x)}+\phi_{WW}\frac{(-\Delta x/2)(\Delta x/2)}{(-2\Delta x)(-\Delta x)}\notag\\ &=\frac{3\phi_P+6\phi_W-\phi_{WW}}{8}\notag \end{align}\\

同理，对于 ee 面，使用W、P和E三个点。那什么时候会用EE呢？就是当 ue<0u_e<0的时候 ee 面会用了。这个是界面上的 ϕ\phi 值。那么一阶导数值如何确定呢？一般仍然使用中心差分，即

(dϕdx)e=ϕE−ϕPΔx\left(\frac{\mathrm{d}\phi}{\mathrm{d}x}\right)_e=\frac{\phi_E-\phi_P}{\Delta x} \\

并且有个很有意思的事情是，我们可以证明：抛物线上的任意两点间的割线斜率，恰等于这两点的中点的切线斜率。这进一步说明了用中心差分获取界面一阶导数值完全没问题。

通用的离散方程V&M上面有，我就不推了。

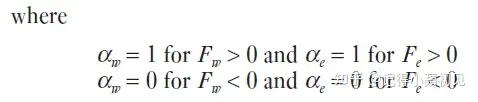
在代码实现的时候，我们认为 Fe=Fw=FF_e=F_w=F，De=Dw=DD_e=D_w=D。

代码部分