通信电子线路-高频功率放大器

 fangda高频功率放大器是一种能量转换器件，将电源供给的直流能量转换成高频交流输出按照工作频带的宽窄划分：窄带高频功率放大器常常用谐振回路作为输出回路——又称调谐功率放大器宽带高频功率放大器输出电路是传输线变压器或者其他宽带匹配电路——非调谐功率放大器

(回顾)小信号功率放大器：

输入信号很小，在微伏到毫伏数量级晶体管工作于线性放大区功率很小，通过阻抗匹配可以获得比较大的增益(30~40dB)一般工作在甲类状态（导通角 θ=180°\theta = 180° )效率比较低

调谐功率放大器：

输入信号大得多工作区域延伸到非线性区域——截止区和饱和区输出功率大一般工作在丙类（导通角 θ<90°\theta < 90° )

调谐功率放大器

调谐功率放大器原理电路

调谐功率放大电路如上图所示：

输入信号（也成为激励信号）经过变压器 T1T_1 耦合到晶体管的基-射极EcE_c 是直流电源电源电压——给集电极提供反向偏置EbE_b 是基极偏置电源电压——提供反向偏置，让晶体管工作在丙类状态LC组成并联谐振回路，称为槽路放大后的信号经过变压器T2T_2 耦合到负载 RLR_L 上

晶体管特性的折线化

三极管的输入特性曲线，来源：https://gss0.baidu.com/7Po3dSag_xI4khGko9WTAnF6hhy/zhidao/wh%3D600%2C800/sign=8e81ac0e78094b36dbc713eb93fc50e1/503d269759ee3d6dead7d51a4d166d224e4adeca.jpg

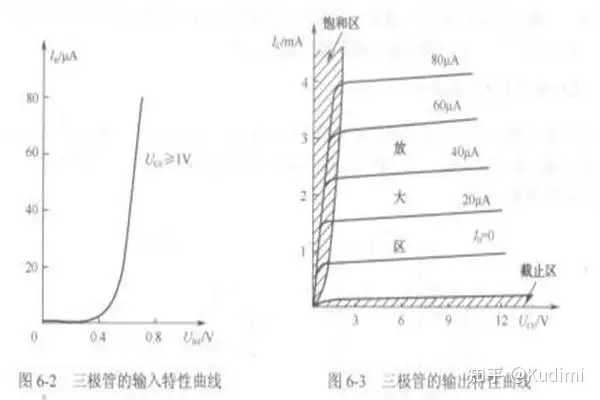
折线化，即将上图所示三极管的特性曲线理想化，用一组折线进行替代，忽略掉特性曲线弯曲部分的影响，上图经过折线化后可以得到效果如下图

折线化后的晶体特性曲线

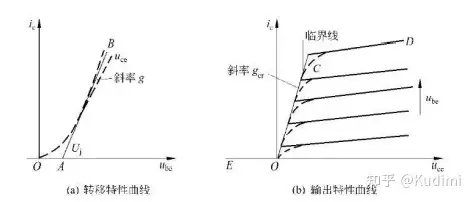
其中：

转移特性曲线用两端直线OA，AB进行近似输出特性曲线则用到三条曲线进行替代即EO，OC，OD输出特性曲线中，斜线OC穿过每一条静态输出特性曲线的拐点（临界点），称为临界线临界线是一条斜率为 gcrg_{cr} 的直线有： ic=gcrucei_c=g_{cr}u_{ce} ic=gcrucri_c=g_{cr}u_{cr} (临界线方程）转移特性曲线的放大区，折线后的AB线斜率为 gg 静态特性曲线可以用方程表示如下： {U_j}} \\ 0&{{u_{be}} < {U_j}} \end{array}} \right.\]">ic={g(ube−Uj)ube>Uj0ube<Uj\[{i_c} = \left\{ {\begin{array}{*{20}{c}} {g({u_{be}} - {U_j})}&{{u_{be}} > {U_j}} \\ 0&{{u_{be}} < {U_j}} \end{array}} \right.\] （理想的静态特性）当放大器在激励电压 ubeu_{be} 和集电极电压 ucu_c 为最大值时：若放大器工作在临界点：放大器工作在临界状态若放大器工作在临界线右边：放大器工作在放大状态若放大器工作在临界线左边即坐标原点和临界线之间任意一点：放大器工作在饱和状态或者过压状态

晶体管导通的特点、导通角

通常把集电极导通时间对应角度的一半称为集电极的导通角，如下图的 θ\theta 调谐功率放大器采用的是反向偏置，偏置的大小为 −Eb-E_b 。在静态的时候，管子处于截止状态( ube<Uju_{be}<U_j)，假定输入信号为 ub=Ubecosωtu_{b}=U_{be}cos\omega t ，当有 U_j">ube=ub−b>Uju_{be}=u_b-b>U_j 的时候，管子导通，集电极电流 ici_c 开始出现和变化，此时对于ub=Ubecosωtu_{b}=U_{be}cos\omega t，晶体管导通时，集电极电流呈现余弦脉冲的形式，晶体管的射、基极电压则为： ube=ub−Ue=Ubmcos⁡ωt−Eb\[{u_{be}} = {u_b} - {U_e} = {U_{bm}}\cos \omega t - {E_b}\] 此时导通角的计算公式可以表示为： cos⁡θ=Uj+EbUbm\[\cos \theta = \frac{{{U_j} + {E_b}}}{{{U_{bm}}}}\] 导通角的示意图推导过程如下：当 ube=ub−Ue=Ubmcos⁡ωt−Eb\[{u_{be}} = {u_b} - {U_e} = {U_{bm}}\cos \omega t - {E_b}\] ，根据三极管的理想静态特性可以得到 ici_c 的表达式： ic=g(Ubmcos⁡ωt−Eb−Uj)\[{i_c} = g({U_{bm}}\cos \omega t - {E_b} - {U_j})\] 。根据导通角的定义：集电极电流导通时间相对应的角度的一半,由于输入的是余弦信号,在t=0时,输入电压最大,此时集电极导通且最大.由于余弦信号的对称性,当变为0时,历经的时间恰好是一个导通角,因此有: ωt=θ,ic=0\[\omega t = \theta ,{i_c} = 0\] 即 ic=g(Ubmcos⁡θ−Eb−Uj)=0\[{i_c} = g({U_{bm}}\cos \theta - {E_b} - {U_j}) = 0\] ，可以解得 θ=arccos⁡Uj+EbUbm\[\theta = \arccos \frac{{{U_j} + {E_b}}}{{{U_{bm}}}}\]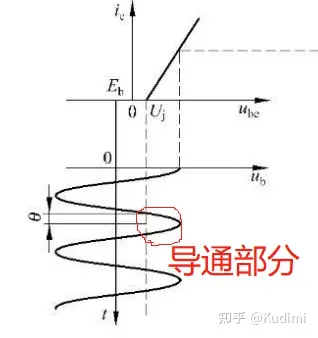

集电极余弦脉冲

已知 ic=g(Ubmcos⁡ωt−Eb−Uj)\[{i_c} = g({U_{bm}}\cos \omega t - {E_b} - {U_j})\] ，导通角的余弦值 cos⁡θ=Uj+EbUbm\[\cos \theta = \frac{{{U_j} + {E_b}}}{{{U_{bm}}}}\] 将后者带入前者可以得到： ic=gUbm(cos⁡ωt−cos⁡θ)\[{i_c} = g{U_{bm}}(\cos \omega t - \cos \theta )\] ，由此可以得到集电极电流的最大值 Icmax\[{I_{c\max }}\] ：Icmax=gUbm(1−cos⁡θ)\[{I_{c\max }} = g{U_{bm}}(1 - \cos \theta )\] 因此集电极电流也可以表示如下：ic=Icmax(1−cos⁡θ)(cos⁡ωt−cos⁡θ)\[{i_c} = \frac{{{I_{c\max }}}}{{(1 - \cos \theta )}}(\cos \omega t - \cos \theta )\] 对集电极电流进行傅里叶函数展开可以得到：ic=Ic0+∑n=1∞Icnmcos⁡nωt\[{i_c} = {I_{c0}} + \sum\limits_{n = 1}^\infty {{I_{cnm}}\cos n\omega t} \] （ ici_c 原是偶函数,因此展开式中不含有sin项）因此有如下：Ic0=12π∫−ππicdωt=Icmaxsin⁡θ−θcos⁡θπ(1−cos⁡θ)Ic1m=1π∫−ππiccos⁡ωtdωt=Icmaxθ−sin⁡θcos⁡θπ(1−cos⁡θ)Icnm=1π∫−ππiccos⁡nωtdωt=Icmax2(sin⁡nθcos⁡θ−ncos⁡nθsin⁡θ)πn(n2−1)(1−cos⁡θ)\[\begin{array}{l} I{}_{c0} = \frac{1}{{2\pi }}\int_{ - \pi }^\pi {{i_c}d\omega t} = {I_{c\max }}\frac{{\sin \theta - \theta \cos \theta }}{{\pi (1 - \cos \theta )}}\\ {I_{c1m}} = \frac{1}{\pi }\int_{ - \pi }^\pi {{i_c}\cos \omega td\omega t} = {I_{c\max }}\frac{{\theta - \sin \theta \cos \theta }}{{\pi (1 - \cos \theta )}}\\ {I_{cnm}} = \frac{1}{\pi }\int_{ - \pi }^\pi {{i_c}\cos n\omega td\omega t} = {I_{c\max }}\frac{{2(\sin n\theta \cos \theta - n\cos n\theta \sin \theta )}}{{\pi n({n^2} - 1)(1 - \cos \theta )}} \end{array}\] 其中： Ic0I_{c0} 是直流分量， Ic1mI_{c1m}是基波分量幅值， IcnmI_{cnm} 是n次谐波分量幅值， IcmaxI_{cmax} 是集电极电流最大值上述式子还可以写成 Icnm=Icmax⋅αn\[{I_{cnm}} = {I_{c\max }} \cdot {\alpha _n}\] 的形式， αn\alpha_n 定义为分解系数：α0=sin⁡θ−θcos⁡θπ(1−cos⁡θ)α1=θ−sin⁡θcos⁡θπ(1−cos⁡θ)α2=2(sin⁡nθcos⁡θ−ncos⁡nθsin⁡θ)πn(n2−1)(1−cos⁡θ)\[\begin{array}{l} {\alpha _0} = \frac{{\sin \theta - \theta \cos \theta }}{{\pi (1 - \cos \theta )}}\\ {\alpha _1} = \frac{{\theta - \sin \theta \cos \theta }}{{\pi (1 - \cos \theta )}}\\ {\alpha _2} = \frac{{2(\sin n\theta \cos \theta - n\cos n\theta \sin \theta )}}{{\pi n({n^2} - 1)(1 - \cos \theta )}} \end{array}\] 傅里叶展开式为：f(x)∼a02+∑n=1∞(ancos⁡nx+bnsin⁡nx)\[f(x) \ \sim\frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {({a_n}\cos nx + {b_n}\sin nx)} \] 各项系数如下：a0=1π∫−ππf(x)dxan=1π∫−ππf(x)cos⁡nxdxbn=1π∫−ππf(x)sin⁡nxdxa\[\begin{array}{l} {a_0} = \frac{1}{\pi }\int_{ - \pi }^\pi {f(x)dx} \\ {a_n} = \frac{1}{\pi }\int_{ - \pi }^\pi {f(x)\cos nxdx} \\ {b_n} = \frac{1}{\pi }\int_{ - \pi }^\pi {f(x)\sin nxdx} a \end{array}\]

槽路电压的分析

uce=Ec−Ucmcos⁡ωt\[{u_{ce}} = {E_c} - {U_{cm}}\cos \omega t\] 其中Ucm\[{U_{cm}}\] 是槽路（抽头部分，即 N0N_0 部分）的电压幅值： Ucm=Ic1mRc=α1IcmaxRc\[{U_{cm}} = {I_{c1m}}{R_c} = {\alpha _1}{I_{c\max }}{R_c}\] RcR_c 是集电极等效负载电阻，是在槽路调谐在基波频率的时候，并联谐振电阻折算到抽头部分的数值：Rc=(N0N1)2R=(N0N1)2QLωLR=R0//RL′=QLωLR0=Q0ωLRL′=(N1N2)2RL\[\begin{array}{l} {R_c} = {(\frac{{{N_0}}}{{{N_1}}})^2}R = {(\frac{{{N_0}}}{{{N_1}}})^2}{Q_L}\omega L\\ R = {R_0}//{R_L}^\prime = {Q_L}\omega L\\ {R_0} = {Q_0}\omega L\\ {R_L}^\prime = {(\frac{{{N_1}}}{{{N_2}}})^2}{R_L} \end{array}\]

高频功放功率和效率的计算

电源供给的直流功率 PS\[{P_S}\] PS=EcIc0=Ec⋅α0Icmax\[{P_S} = {E_c}{I_{c0}} = {E_c} \cdot {\alpha _0}{I_{c\max }}\] (集电极电压和集电极直流分量的乘积 )其中Ec是集电极电压，Ic0是直流分量α0\[{\alpha _0}\] 是直流分解系数， IcmaxI_{cmax} 是集电极电流的最大值 晶体管集电极输出的交流功率 PoP_o Po=12UcmIc1m=12Ucm⋅α1IcmaxPo=Ucm22R=Ucm22QLωL\[\begin{array}{l} {P_o} = \frac{1}{2}{U_{cm}}{I_{c1m}} = \frac{1}{2}{U_{cm}} \cdot {\alpha _1}{I_{c\max }}\\ {P_o} = \frac{{{U_{cm}}^2}}{{2R}} = \frac{{{U_{cm}}^2}}{{2{Q_L}\omega L}} \end{array}\] (基波分量在槽路的平均功率)其中R是LC回路两端的总电阻，QL是有载品质因数α1\alpha_1 是基波分解系数， IcmaxI_{cmax} 是集电极电流的最大值(槽路电压就是基波分量在集电极上形成的压降) 通过槽路送给负载的交流功率 PL\[{P_L}\] PL=Po−PTP_L=P_o-P_T 晶体管在能量转换过程中的损耗功率 PcP_c Pc=Ps−PoP_c=P_s-P_o 槽路损耗功率 PTP_T PT=Ucm22R0=Ucm22Q0ωL\[{P_T} = \frac{{{U_{cm}}^2}}{{2{R_0}}} = \frac{{{U_{cm}}^2}}{{2{Q_0}\omega L}}\] (槽路损耗功率是槽路空载电阻R0吸收的功率)集电极效率晶体管转换能量的效率称集电极效率（把电源供给的直流功率转换成集电极输出的交流功率）计算公式为： ηc=PoPS=12Ucm⋅α1IcmaxEc⋅α0Icmax=12α1α0UcmEc\[{\eta _c} = \frac{{{P_o}}}{{{P_S}}} = \frac{{\frac{1}{2}{U_{cm}} \cdot {\alpha _1}{I_{c\max }}}}{{{E_c} \cdot {\alpha _0}{I_{c\max }}}} = \frac{1}{2}\frac{{{\alpha _1}}}{{{\alpha _0}}}\frac{{{U_{cm}}}}{{{E_c}}}\] 极限情况下 α1α0=2\[\frac{{{\alpha _1}}}{{{\alpha _0}}} = 2\] UcmEc\[\frac{{{U_{cm}}}}{{{E_c}}}\] 称为集电极电压利用系数记为 ξ\[\xi \] 槽路效率 槽路将交流功率传送给负载的效率叫槽路效率计算公式为:ηT=PLPo=Po−PTPo=Ucm2QLωL−Ucm2Q0ωLUcm2QLωL=Q0−QLQ0\[{\eta _T} = \frac{{{P_L}}}{{{P_o}}} = \frac{{{P_o} - {P_T}}}{{{P_o}}} = \frac{{\frac{{{U_{cm}}^2}}{{{Q_L}\omega L}} - \frac{{{U_{cm}}^2}}{{{Q_0}\omega L}}}}{{\frac{{{U_{cm}}^2}}{{{Q_L}\omega L}}}} = \frac{{{Q_0} - {Q_L}}}{{{Q_0}}}\] 取决于槽路的有载品质因数和无载品质因数Q0Q_0 不能很大：元件的限制Q0Q_0 不能太小：选频特性会差

调频功放动态特性的作图法

调谐功放的动态特性曲线图有下导出：ic=g(ube−Uj)(1)ube=ub−Eb=Ubmcos⁡ωt−Eb(2)uce=Ec−Ucmcos⁡ωt(3)\[\begin{array}{*{20}{c}} {{i_c} = g({u_{be}} - {U_j})}&{(1)}\\ {{u_{be}} = {u_b} - {E_b} = {U_{bm}}\cos \omega t - {E_b}}&{(2)}\\ {{u_{ce}} = {E_c} - {U_{cm}}\cos \omega t}&{(3)} \end{array}\] (1)称为内部特性方程，(2)、(3)称为外部特性方程，由3者可以得到：ic=g(−Eb−Uj+UbmEc−uceUcm)\[{i_c} = g( - {E_b} - {U_j} + {U_{bm}}\frac{{{E_c} - {u_{ce}}}}{{U{}_{cm}}})\] 调谐功放的动态函数，描述不同参数下ic的变化情况是一条直线Q点：静态工作点（直流工作点）此时交流分量为0是个假想点在 uce−icu_{ce}-i_c 图像上的坐标点为 : Q=(Ec,−g(Eb+Uj))\[Q = ({E_c}, - g({E_b} + {U_j}))\] B点：起始导通点此时集电极电流 恰好为0B点在 uce−icu_{ce}-i_c 图像上的坐标点为: B=(Ec−Ucmcos⁡θ,0)\[B = ({E_c} - U{}_{cm}\cos \theta ,0)\] 其中 θ\theta 是管子的导通角C点：放大区动态线端点—BQ所在直线和 的交点此时 uceu_{ce} 是一个极值点，取值为 Ec−UcmE_c-U_{cm} C点在 uce−icu_{ce}-i_c 图像上的坐标点为 C=(Ec−Ucm,g(Ubm−Eb−Uj))\[C = ({E_c} - {U_{cm}},g({U_{bm}} - {E_b} - {U_j}))\] CB段是晶体管处于放大区的动态线 当晶体管工作在过压状态时候, Ec−Ucm\[{E_c} - U{}_{cm}\] 对应的 uceu_{ce} 会落入饱和区，C点不再恰好处于动态线和饱和线的交点，而是会沿着饱和线向O点偏移，此时动态线有部分和饱和线重合 A点：此时 uceu_{ce} 是另一个极值点，取值为 Ec+UcmE_c+U_{cm} ，落入截止区A点在 uce−icu_{ce}-i_c 图像上的坐标点为 A=(Ec+Ucm,0)\[A = ({E_c} + {U_{cm}},0)\] AB段是晶体管处于截止状态的动态线

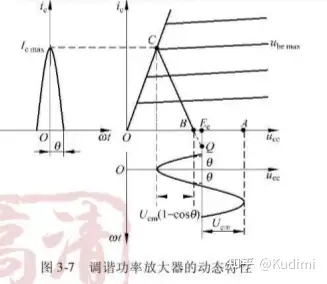
调谐功放工作状态

过压（超过饱和压降线）状态晶体管工作时有部分时间进入饱和区即 ucemax=Ec−Ucm\[{u_{ce\max }} = {E_c} - {U_{cm}}\] 落入饱和区有: ucemax=Ec−Ucm<Uces\[{u_{ce\max }} = {E_c} - {U_{cm}} < {U_{ces}}\] 临界状态 晶体管工作时，恰好不进入饱和区即 在临界点有:ucemax=Ec−Ucm=Uces\[{u_{ce\max }} = {E_c} - {U_{cm}} = {U_{ces}}\] 欠压状态晶体管工作时，完全不进入饱和区即 大于临界点有：{U_{ces}}\]">ucemax=Ec−Ucm>Uces\[{u_{ce\max }} = {E_c} - {U_{cm}} >{U_{ces}}\] UcesU_{ces} 是晶体管的饱和压降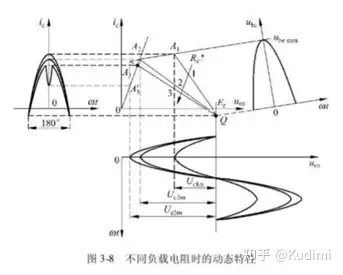 已知ucemax=Ec−Ucm\[{u_{ce\max }} = {E_c} - {U_{cm}}\] ，又 Ucm=α1IcmaxRc\[{U_{cm}} = {\alpha _1}{I_{c\max }}{R_c}\] ，根据不同的 RcR_c 可以得到经过相同静态工作点Q的不同的动态特性曲线： QA1:欠压状态集电极电流是余弦脉冲 QA2:临界状态集电极电流仍然是余弦脉冲，只不过幅值比欠压略小QA3A3′QA_3A_3 :过压状态集电极电流呈现马鞍状（由于工作点进入饱和区）

调谐功放的负载特性

不同工作状态下电流、电压和RC的关系：欠压状态 RcR_c 增大：IcmaxI_{cmax} 和 θ\theta 略有减小、Ic0、Ic1mI_{c0}、I_{c1m} 也有所减小（接近常量à可以视为恒流源）因此Ucm的变动近乎和RC相同临界状态/过压状态Rc增大：波形下凹下降较快 ､Ic0､Ic1mI_{c0}､I_{c1m} 也很快下降,Rc增大越多,下降越快Ucm仍略有增加（接近不变à可以视为恒压源）不同工作状态下功率、效率和Rc的关系： 功率和Rc的关系： 欠压状态Rc增大：Po=12Ic1m2Rc\[{P_o} = \frac{1}{2}I_{c1m}^2{R_c}\] ， Ic1mI_{c1m} 有所减小但接近常量, PoP_o 增大 Ps=EcIc0P_s=E_cI_{c0} ， EcE_c 是常量， Ic0I_{c0} 有所下降， PSP_S 有所下降过压状态:Po=Ucm2Rc\[{P_o} = \frac{{U_{cm}^2}}{{{R_c}}}\] ， Ucm2\[U_{cm}^2\] 接近常数，因此 PoP_o 减小PS=EcIc0P_S=E_cI_{c0} ， EcE_c 是常量， Ic0I_{c0} 下降增快， PSP_S 下降增快 临界状态下输出功率最大 效率和Rc的关系：欠压状态Rc增大:ηc=PoPS\[{\eta _c} = \frac{{{P_o}}}{{{P_S}}}\] , PoP_o 增大 , PSP_S 有所下降, ηc\eta_c 增大过压状态Rc增大ηc=PoPS\[{\eta _c} = \frac{{{P_o}}}{{{P_S}}}\] ， PoP_o 减小， PSP_S 下降增快，刚过临界点时, PoP_o 减小的没有 PSP_S 快，因此 ηc\eta_c 仍在增加，到达某个临界点后开始下降ηc\eta_c 的最大值出现在弱过压区

基极调制特性

、、Ec、Ubm、RcE_c、U_{bm}、R_c 恒定的时候， 对放大器工作状态的影响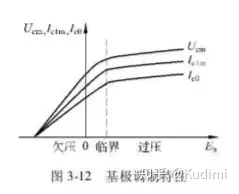 Rc不变，动态负载特性曲线的斜率不变，Ec不变，静态工作点不变由于 ubmmax=Ubm−Ebu_{bmmax}=U_{bm}-E_b ，因此动态工作曲线随着 EbE_b 的改变而改变欠压状态时：随着 EbE_b 的变化 ,ubemaxu_{bemax} 变化，放大区动态线端点—BQ所在直线和 ubemax=Ubm−Ebu_{bemax}=U_{bm}-E_b的交点发生变化， ici_c 变化范围较大，因此 、、Ucm、Ic0、Ic1U_{cm}、I_{c0}、I_{c1} 变化也比较大过压状态时：放大区动态线端点—BQ所在直线和 ubemax=Ubm−Ebu_{bemax}=U_{bm}-E_b 的交点落入饱和区，实际动态线部分和饱和线重合， ici_c 变化范围较小因此采用基极调幅的时候，应该工作在欠压区

集电极调制特性

、、Eb、Ubm、RcE_b、U_{bm}、R_c 恒定的时候， EcE_c 对放大器工作状态的影响 Rc不变，动态负载特性曲线的斜率不变，因为 EbE_b 不变， UbmU_{bm} 不变，因而对应于 uceminu_{cemin} 的动态点就在 ube=ubemaxu_{be}=u_{bemax} 上移动。EcE_c 变化, uceminu_{cemin} 也随之变化 当 EcE_c 比较大的时候, uceminu_{cemin} 也比较大,不落入饱和区,管子工作在欠压状态: 此时随着 EcE_c 的变化, ici_c 的变化比较小（基本不变） 当 EcE_c 比较小的时候, uceminu_{cemin} 也比较小,落入饱和区,管子工作在过压状态:此时随着 EcE_c 的变化，进入饱和区后， ici_c 的大小会沿着饱和线下降，近乎线性变化，波型变成中间凹陷的脉冲波，此时 EcE_c 对 ici_c 的控制作用明显，即 EcE_c 对 、、Ucm、Ic0、Ic1mU_{cm}、I_{c0}、I_{c1m} 的控制作用也明显采用集电极调幅的时候，应该让管子工作在过压区

集电极馈电电路/直流馈电电路

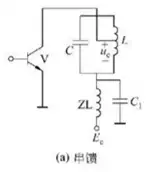
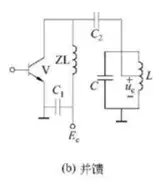
串馈电路：串馈电路旁路电容直接接地，因此馈电支路的分布参数不会影响谐振回路的工作频率，适用于频率比较高的情况谐振回路处于直流高电位上，谐振回路元件不能直接接地，调整不便 串馈集电极旁路电容 C1C_1 计算如下：xC1=15∼20RC\[{x_{{C_1}}} = \frac{1}{{5\sim20}}{R_C}\] 扼流圈ZL的电抗计算：xZL1=(5∼20)RC\[{x_{Z{L_1}}} = (5\sim20){R_C}\] 其中 RCR_C 是输出回路的有载等效阻抗 并馈电路：有C2的存在，隔断直流，谐振回路处于直流的电位上，滤波元件可以直接接地 高频扼流圈ZL，隔直电容C2在高频写对调谐回路有影响，馈电支路的分布电容使得c-e端总电容增大，限制了放大器在更高频段工作隔直电容C2对于工作频率应该近乎短路：\[{x_{{C_1}}} = \frac{1}{{5\sim20}}{R_C}\] 扼流圈的大小应该为：\[{x_{Z{L_1}}} = (5\sim20){R_C}\]

自给偏压环节

射极电流自给偏压环节射极电流的直流成分 I_{e0} 通过电阻 R_e 形成的电压 I_{e0}R_e ，其极性对晶体管是一个反偏压（实现对基极加入反偏电压）(a)适用于有直流通路的情况(b)适用于没有直流通路的情况 电阻 R_e 的大小由以下公式给出：\[{R_e} = \frac{{{E_b}}}{{{I_{e0}}}}\] 放电时间应该足够大，保证偏压不随交流波动：\[{R_e}{C_e} \ge \frac{5}{f}\] 基极电流自给偏压环节 * 基极直流电流 通过基极电阻 形成压降,在基极形成反向偏压(a)适用于信号源不含有直流成分的情况(b)适用于信号源没有直流通路的情况，ZL防止信号被Cb短路 基极电阻的大小由下式子给出：\[{R_e} = \frac{{{E_b}}}{{{I_{e0}}}}\] 对于并联的电容有如下要求：\[{R_e}{C_e} \ge \frac{5}{f}\]

并连谐振回路的匹配

多用于前级、中间级放大器和需要可调电路的输出级放大器工作在临界状态的时候输出功率 P_o 最大，因此放大器在临界状态的等效电阻大小，就是放大器阻抗匹配所需的负载电阻 计算过程如下：先估算管子的饱和压降，然后得到临界状态槽路抽头部分的电压幅值：U_{cm}=E_c-U_{ces} (此式子得出的就是临界态下对应的抽头部分电压幅值） 确定最佳负载电阻 已知输出功率的计算公式： \[{P_o} = \frac{{{U_{cm}}^2}}{{2{R_c}}} = \frac{{{U_{cm}}^2}}{{2{R_{cp}}}}\] 临界状态的时候有：\[{R_c} = {R_{cp}} = \frac{{{U_{cm}}^2}}{{2{P_o}}} = \frac{{{{({E_c} - {U_{ces}})}^2}}}{{2{P_o}}}\] 式子中一般 P_o 是要求值，会给出限定E_c、U_{ces} 也是恒定值匝数比的选择 实际电路中要让集电极电阻等于外加负载R_c=R_{cp} ： 因为 \[{R_c} = {(\frac{{{N_0}}}{{{N_1}}})^2}{Q_L}\omega L\] (其中 N_0 是全电感匝数 N_1 是抽头匝数) 所以改变自耦变压器的匝数比就能使得R_c=R_{cp} 所需要的自耦电感匝数比为：\[\frac{{{N_0}}}{{{N_1}}} = \sqrt {\frac{{{R_c}}}{{{Q_L}\omega L}}} \] 对于互感变压器的匝数比 \[\frac{{{N_2}}}{{{N_1}}}\] ，以为其值的改变会引起槽路电阻 R_c 和有载品质因数 Q_L 的改变，值应该依据有载品质因数的值 Q_L 进行选取：\[{Q_L}\omega L = {R_0} + {R_L}^\prime = ({Q_0}\omega L)//[{(\frac{{{N_1}}}{{{N_2}}})^2}{R_L}] = \frac{{({Q_0}\omega L)[{{(\frac{{{N_1}}}{{{N_2}}})}^2}{R_L}]}}{{({Q_0}\omega L) + [{{(\frac{{{N_1}}}{{{N_2}}})}^2}{R_L}]}}\] 解得匝数比大小为：\[\frac{{{N_2}}}{{{N_1}}} = \sqrt {\frac{{{Q_0} - {Q_L}}}{{{Q_0}}}\frac{{{R_L}}}{{{Q_L}\omega L}}} = \sqrt {{\eta _T}\frac{{{R_L}}}{{{Q_L}\omega L}}} \]

倍频器

将输入信号频率成整数倍增加的电路，一般用于中间级 使用倍频器： 降低设备的主振频率 可以增加条制度，加大相移或频移 利用倍频器拓展发射机输出级的工作波段 丙类倍频器的集电极谐振回路是对输入频率 f_i 的n倍频谐振，而其他谐波（包括基波）被滤除 工作原理 假定输入的电压是：u_{be}=U_{bm}cos\omega t-E_b 输出的电压是：u_{ce}=E_c-U_{cm}cos\omega t 此时谐振回路两端的交流电压为：U_{cm}cosn\omega t 输出的功率以及集电极效率是：\[\begin{array}{l} {P_{on}} = \frac{1}{2}{U_{cnm}}{I_{cnm}} = \frac{1}{2}{U_{cnm}}{\alpha _n}{I_{c\max }} = \frac{1}{2}\frac{{{U_{cnm}}^2}}{R}\\ {\eta _{cn}} = \frac{{\frac{1}{2}{U_{cnm}}{I_{cnm}}}}{{{E_c}{I_{c0}}}} = \frac{1}{2}\frac{{{U_{cnm}}{\alpha _n}}}{{{E_c}{\alpha _0}}} \end{array}\] 无论导通角为何值，丙类倍频器的输出功率和效率远小于丙类放大器，并且随着n的增大而迅速降低保证最大输出功率和最佳效率：要加大倍频器的输入电压和基极偏压增加谐振回路的等效阻抗 提高频率倍数一般采用多级倍频器