如何计算出自然常数 e 的值？（数学学习 035）-自然常数e的相关公式

 

如何计算出自然常数 e 的值？（数学学习 035）

01

我们先来回顾一下这几天学习的东西。

我们知道，到目前为止，我们接触到的数学，从本质上讲，只有“加”与“乘”。而“加”与“乘”，一共有四种组合，加加、加乘、乘加与乘乘。

我们在探讨“加乘”组合的时候，发现了有一个极其特殊（Extremely special）的函数，并缩写为极其特殊这个单词的首字母 E(x) 。

这个函数特殊之处在于：

第一，这个函数的导数，就是其自身。即

E(x)=E(x)

第二，这个函数，可以表示为某个数的 x 次方。我们将这个极其特殊的数字，用 e 表示，即

E(x)=ex

我们不知道这个“极其特殊”的数 e 到底如何取值？

昨天也提到过，像这种情况，我们知道某个函数的某些性质和某些点的值，但不知道这个函数应该如何准确地描述，一般都需要用到“泰勒级数”。

现在，我们又处于这种情况。我们对于 E(x) 这个函数的准确描述，只差知道 e 的值是多少。因此，求出 e 的值，这个函数就被准确描述了。

好，泰勒级数用起来。

02

嗯，是不是应该先回顾一下什么是泰勒级数？

首先，函数有一个一般表达式：

f(x) = c0x0+c1x1+…+cnxn

（依此继续）

其次，通过不断求导，能够准确得出 cn 的取值。

cn= f(n)(x)/n！

最后，将 cn 的取值代入通用函数表达式。即

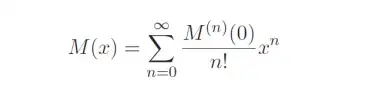
这就是泰勒级数（ Taylor series ）。

我们将 E(x) 函数用泰勒级数来表示。即

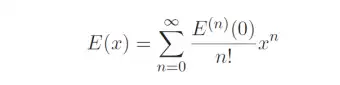
前面说了， E(x) 的极其特殊之处，是导数是其自身。即

E(x)=E(x)

那么，无论求导多少次，也就是不断地求导，结果还是其自身。即

E(n)(x)=E(x)

也就是说

E(n)(0)=E(0)

而我们又恰好知道 E(x)=ex 即

E(0)= e0=1

那么， E(x) 用泰勒级数表示就变更为以下表达式

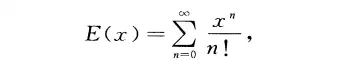
如果把这个表达式拉开，则

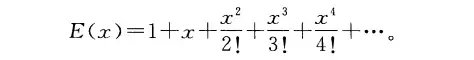
看起来很好玩。我们来检验一下。先看看它的导数是不是自身？

这很简单，就是一项一项单独求导。

1=0

x=1

(x2/2!)=2x/2!

(x3/3!)=3x2/3!

(x4/4!)=4x3/4!

……

而 n! = n(n-1)(n-2)…(3)(2)(1)

也就是说

OK ，完全正确。

03

那么， e 是多少呢？

因为 E(x)=ex ，那么，当 x=1 时，E(x)= e 。即

e=1+1+1/2!+1/3!+…

也可以表示为

可以看出，这是一个比 2 大，比 3 小的数，到底是多少呢？

我们可以一项一项去计算，然后加总起来就对了。

但是，问题在于， n 是无穷的啊，怎么可能一项一项地计算呢？

或许应该换一种方法。

试试利用导数是其自身这个特征。

ex=(ex)

=(ex+dx-ex)/dx

=ex(edx-1)/dx

两边同时除以 ex 。则

edx-1= dx ，即

edx= dx+1 ，

两边指数同时乘以 1/dx ，即

e= (1+dx)1/dx

令 N=1/dx ，则

e= (1+1/N)N

其中， N 为无穷大，因为 dx 是无穷小。因此，我们也可以表示为：

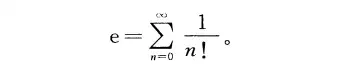
04

对于数学来说，做到这一步就已经完成了。因为萨穆伊尔·施恰图诺夫斯基(Samuil Shchatunovski) 说过：

数学的任务不是……把算术做对。那是银行会计的工作。

（It is not the job of mathematicians…to do correct arithmetical operations. It is the job of bank accountants.）

但对于我们一般人来说，这不行啊，我们还是想知道 e 的具体数值啊。

请出计算机来自动计算吧。这里直接说结果。

如果用公式一

e=1+1+1/2!+1/3!+…

计算前 100 项的结果，精确到小数点后 9位，是 2.718281828 。

计算前 1,000,000,000 项的结果，精确到小数点后 9 位，依然是 2.718281828 。

如果用公式二

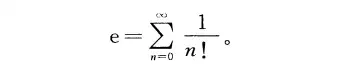
计算 N=100 时，精确到小数点后 9 位，结果是 2.704813829 。

N=1,000,000,000 时，精确到小数点后 9 位，结果是 2.718281827 。

OK ，我们知道了， e 大概就是约等于 2.718281828 。