xgboost原理？

更好的阅读体验请点击原文链接：科赛 - Kesci.com

以下是正文~

简介

在大数据竞赛中,XGBoost霸占了文本图像等领域外几乎80%以上的大数据竞赛.当然不仅是在竞赛圈,很多大公司也都将XGBoost作为核心模块使用,好奇的人肯定都很想揭开这个神奇的盒子的幕布,究竟是里面是什么,为什么这么厉害? 本篇notebook会从理论和实践的角度来讲述XGBoost以及关于它的一段历史与组成。

此处我们会按照下图的形式来讲述关于XGBoost的进化史.

CART(Classification and Regression Tree)

CART的全称是Classification and Regression Tree,翻译过来就是分类与回归树,是由四人帮Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出的,该算法是机器学习领域一个较大的突破,从名字看就知道其既可用于分类也可用于回归.

CART本质是对特征空间进行二元划分(即CART生成的决策树是一棵二叉树),它能够对类别变量与连续变量进行分裂,大体的分割思路是：

分裂指标（分类树：Gini指数）

在CART分割时,我们按照 GiniGini指数最小来确定分割点的位置. 例子

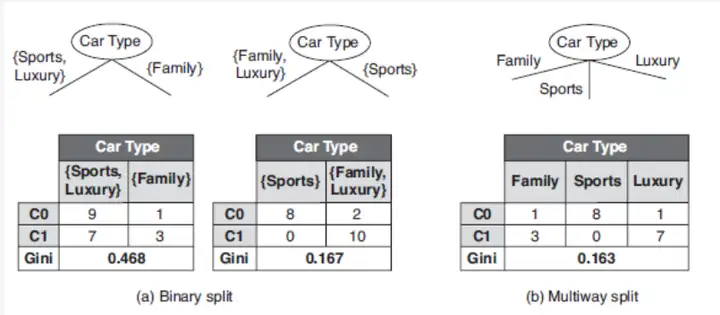
对于Categorical变量

数据集关于第一个特征维度的 GiniGini 指数的计算(其他的类似)就是: Gini(D,CarType)=9+79+7+1+3[2∗99+7∗(1−99+7)]+1+39+7+1+3[2∗11+3∗(1−11+3)]=0.468Gini(D,CarType) = \frac{9+7}{9+7+1+3}[ 2 * \frac{9}{9+7}* (1 - \frac{9}{9+7}) ] + \frac{1+3}{9+7+1+3}[ 2 * \frac{1}{1+3}* (1 - \frac{1}{1+3})] = 0.468

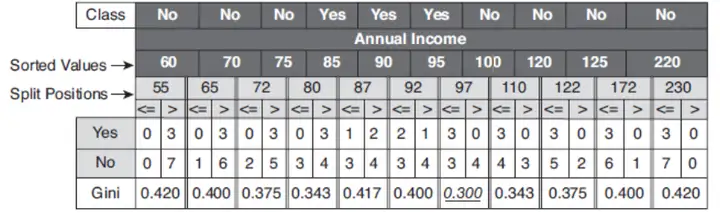
对于连续变量

因为连续变量的部分已经通过某一个值进行了划分,所以计算的时候和Categorical变量的计算类似.

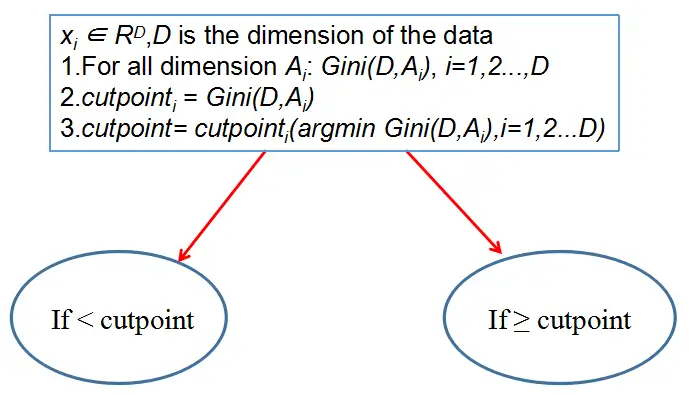
CART分割示意图

下图的 Gini(D,Ai)Gini(D,Ai) 默认为第 ii 个特征维度的最小 GiniGini 值.

CART算法(分类树,无剪枝)

根据训练数据集,从根节点开始,递归地对每个结点进行以下操作,构建二叉决策树:

(1) 设结点的训练数据集为 DD ,计算现有特征对该数据集的基尼指数( GiniGini ),此时,对每一个特征A,对其可能取的每个值 aa(先排序),根据样本点对 A=aA=a 的测试"是"或"否"将 DD 分割成 D1,D2,D_1,D_2, 计算当 A=aA=a 时的基尼指数;

(2) 在所有可能的特征 AA 以及它们所有可能的切分点 aa 中,选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点,依最优特征与最优切分点,从现节点生成两个子节点,将训练数据集依特征分配到两个子节点中去;

(3) 对两个子节点递归调用(1),(2),直至满足停止条件.

(4) 生成CART决策树.

CART（回归树部分）

在训练数据集所在的输入空间中,递归地将每个区域划分为两个子区域并决定每个子区域的输出值,构建二叉决策树:

(1) 选择最优切分变量j与切分点s,求解:minj,s[minc1Σxi∈R1(j,s)(yi−c1)2+minc2Σxi∈R2(j,s)(yi−c2)2min_{j,s}[min_{c_1} \Sigma_{x_i \in R_1(j,s)} (y_i -c_1)^2 + min_{c_2} \Sigma_{x_i \in R_2(j,s)} (y_i - c_2)^2 遍历变量 jj , 对固定的切分变量j扫描切分点s,选择使得上式达到最小值的对 (j,s)(j,s) .

(2) 用选定的对 (j,s)(j,s) 划分区域并决定相应的输出值:

s \}">R1(j,s)={x|x(j)≤s},R2(j,s)={x|x(j)>s}R_1(j,s) = \{x | x^{(j)} \le s\}, R_2(j,s) = \{x | x^{(j)} > s \}

c¯m=1NmΣxi∈Rm(j,s)yi,x∈Rm,m=1,2\bar{c}_m = \frac{1}{N_m} \Sigma_{x_i \in R_m(j,s)}y_i, x \in R_m, m=1,2

(3) 继续对两个子区域调用(1),(2),直至满足停止条件.

(4) 将输入空间划分为 MM 个区域 R1,R2,...,RMR_1,R_2,...,R_M ,生成决策树: f(x)=Σm=1Mc¯mI(x∈Rm)f(x) = \Sigma_{m=1}^M \bar{c}_m I(x \in R_m) 附录

Boosting

上面是最常用的树模型的介绍,现在我们要介绍Boosting技术,Boosting在维基百科上面的解释是:

实际生活中,人们也常用"三个臭皮匠赛过诸葛亮"的话来描述Boosting(提升方法).当然这背后还有理论的支撑与保障,两个大牛Kearns和Valiant提出了强可学习和弱可学习概念同时在此概念下,Schapire证明的强可学习与弱可学习是等价的伟大理论[9]. 服从Boosting维基百科的解释,我们用简单的数学对其进行表示,

现在我们要将多个弱分类器转化为强分类器 F(x)F(x) .怎么转换呢？最直接的就是线性加权: F(x)=Σi=1Mαifi(x)F(x) = \Sigma_{i=1}^M \alpha_i f_i(x) ,其中 αi\alpha_i 为第 ii 个分类器的权重, 当然我们也可以将其进一步变形为: F(x)=Σi=1Mαifi(x)=Σi=1Mgi(x)F(x) = \Sigma_{i=1}^M \alpha_i f_i(x) = \Sigma_{i=1}^{M} g_i(x) ，其中 gi(x)=αifi(x)g_i(x) = \alpha_i f_i(x)

Boosting Tree

将上面的Boosting思想和树进行结合,我们便得到了提升树的简易版本.

F(x)=Σi=1Mgi(x)=Σi=1Mg(x,θi)$,$g(x,θi)F(x) = \Sigma_{i=1}^{M} g_i(x) = \Sigma_{i=1}^{M} g(x,\theta_i) $, $g(x,\theta_i) 是第i棵树， θi\theta_i 是第 ii 棵树的参数.我们就得到了Boosting Tree的表达形式.但是这样的形式该如何求解得到呢.....

Boosting的基本思想

按照所有的监督机器学习算法的模式,我们需要通过训练获得的 F(x)F(x) ,使得对于给定的输入变量 xx ,我们输出的 F(x)F(x) 都能较好地近似 yy .换言之,就是希望我们的损失函数: L(y,F(x))L(y, F(x)) 尽可能的小.

如果从传统的平方损失函数的角度出发的话就是:

希望对于所有的样本, min1NΣi=1N(yi−F(xi))2min \frac{1}{N}\Sigma_{i=1}^N(y_i - F(x_i))^2 ,写成向量的形式就是 min1N(y−F(x))2min \frac{1}{N}(y - F(x))^2 . 因为 F(x)F(x) 是由多个含有不同参数的弱分类器组成,我们无法向传统的梯度下降的形式进行直接的优化, 不过不急, 我们慢慢分析, 一步一步来.

我们的目标是最小化 min(y−F(x))2min (y-F(x))^2 , yy 是向量的形式,包含所有样本的label.

① 我们构造 f1(x)f_1(x) 希望 (y−f1(x))2(y-f_1(x))^2 尽可能的小.

② 我们训练 f2(x)f_2(x) 希望 (y−f1(x)−f2(x))2(y-f_1(x)-f_2(x))^2 尽可能的小.

③ 我们训练 f3(x)f_3(x) 希望 (y−f1(x)−f2(x)−f3(x))2(y-f_1(x)-f_2(x)-f_3(x))^2 尽可能的小.

......依次类推,直至第 fM(x)f_M(x) .

从上面的构造角度看,我们发现构建第 t+1t+1 个分类器的时候,前 tt 个分类器是固定的,也就是说在第 t+1t+1 步,我们的目标就是 min(y−Σj=1tfj(x)−ft+1(x))2min (y-\Sigma_{j=1}^tf_j(x) - f_{t+1}(x))^2

我们令 r=y−Σj=1tfj(x)r = y - \Sigma_{j=1}^tf_j(x) 表示我们的残差,而我们的下一个分类器 ft+1(x)f_{t+1}(x) 就是尽可能拟合我们的残差 rr . 使得 (y−Σj=1tfj(x)−ft+1(x))2=(r−ft+1(x))2<(y−Σj=1tfj(x))2(y-\Sigma_{j=1}^tf_j(x) - f_{t+1}(x))^2 = (r - f_{t+1}(x))^2< (y-\Sigma_{j=1}^tf_j(x))^2 ,这样我们每次迭代一轮,损失误差就会继续变小,在训练集上离我们的目标也就更加近了.

从而我们得到我们的梯度提升树算法.

提升树算法 (回归问题)

(1) 初始化 f0(x)=0f_0(x) = 0

(2) 对 m=1,2,...,Mm=1,2,...,M

(a) 计算残差, rmi=yi−Fm−1(xi),i=1,2,3,...,Nr_{mi} = y_i - F_{m-1}(x_i), i=1,2,3,...,N

(b) 拟合残差 rmir_{mi} 学习一个回归树,得到 fm(x)f_m(x)

(c) 更新 fm(x)=Fm−1(x)+fm(x)f_m(x) = F_{m-1}(x) + f_m(x)

(3) 得到回归问题提升树 FM(x)=Σi=1Mfi(x)F_M(x) = \Sigma_{i=1}^M f_i(x)

问题

上面我们使用的是简单的平方损失函数的形式对我们的目标进行了展开与化简,但我们实际中却有很多其他的损失函数,而且在很多问题中,这些损失函数比我们的平方损失函数要好很多.

同样的, 我们的方法仍然不变,是希望在第 t+1t+1步的时候学习分类器 ft+1(x)f_{t+1}(x)使得 L(y,Σj=1tf(x)+ft+1(x))L(y,\Sigma_{j=1}^t f(x) + f_{t+1}(x)) 尽可能的在 L(y,Σj=1tf(x))L(y,\Sigma_{j=1}^t f(x))的基础上面变得更小.

这个时候我们发现无法像上面那样直接展开并进行残差拟合了......那该怎么办呢？

Gradient Boosting Decision Tree(梯度提升树)

Gradient Boosting的基本思想

接着上面的问题,我们退回来想一想,因为我们的目标是最小化 L(y,F(x))L(y,F(x)) ,所以我们只需要 L(y,Σj=1tfj(x)+ft+1(x))L(y,\Sigma_{j=1}^t f_j(x) + f_{t+1}(x)) 的值比 L(y,Σj=1tfj(x))L(y,\Sigma_{j=1}^t f_j(x)) 小,好了,既然这样,貌似问题又出现了一丝曙光, 那现在我们再假设,我们的损失函数$L$是可导的,这个假设很合理,毕竟现在90%以上的损失函数都是可导的.是不是感觉至少该问题又可以求解了.

那么我们现在的目标就变成了 ：

max[(L(y,Σj=1tfj(x))−L(y,Σj=1tfj(x)+ft+1(x)))] max [(L(y, \Sigma_{j=1}^t f_j(x)) - L(y, \Sigma_{j=1}^t f_j(x) + f_{t+1}(x)))] ,为了方便,我们令 c=Σj=1tfj(x)c = \Sigma_{j=1}^t f_j(x) , 好吧,既然如此, max[L(y,c)−L(y,c+ft+1(x))]max [L(y, c) - L(y,c+f_{t+1}(x))] .

L(c+ft+1(x))≈L(c)+L′(c)ft+1(x)L(c+ f_{t+1}(x)) \approx L(c) + L(c) f_{t+1}(x)

L(c+ft+1(x))=L(c)+L′(c)ft+1(x)=L(c)−L′(c)2<L(c)L(c+ f_{t+1}(x)) = L(c) + L(c) f_{t+1}(x) = L(c) - L(c) ^2 < L(c) ,其中 ft+1(x)=−1∗L′(x) f_{t+1}(x) = -1 * L(x)

→→→\rightarrow \rightarrow \rightarrow 现在我们用 fi+1(x)f_{i+1}(x) 来拟合 ft+1(x)=−1∗L′(x) f_{t+1}(x) = -1 * L(x) , 原先的 rr 就变成了现在的梯度！ Nice! 于是梯度提升树就产生了.

梯度提升树算法

(1) 初始化 f0(x)=argmincΣi=1NL(yi,c)f_0(x) = argmin_c \Sigma_{i=1}^N L(y_i,c)

(2) 对 m=1,2,...,Mm=1,2,...,M

(a) 对 i=1,2,...,N$i =1,2,...,N$ ,计算， $rmi=−[∂L(yi,f(xi))∂f(xi)]f(x)=Fm−1(x) $r_{mi} = - [\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)}]_{f(x) = F_{m-1}(x)}

(b) 拟合残差 rmir_{mi} 学习一个回归树,得到 fm(x)f_m(x)

(c) 更新 Fm(x)=Fm−1(x)+fm(x)F_m(x) = F_{m-1}(x) + f_m(x)

(3) 得到回归问题提升树 FM(x)=Σi=0Mfi(x)F_M(x) = \Sigma_{i=0}^M f_i(x)

注意

上面提到的梯度提升树是最简易的版本,后续写在各种开源包中的GBDT都在残差的部分增加了步长(或者学习率), rmi=−r_{mi} = - αm\alpha_m[∂L(yi,f(xi))∂f(xi)]f(x)=Fm−1(x)[\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)}]_{f(x) = F_{m-1}(x)} , 用学习率来控制我们模型的学习速度,和传统的梯度下降的方式类似.

XGBoost与传统GBDT的算法层面的区别

XGBoost中的GBDT与传统的GBDT在算法层面有主要有两处较大的不同:

XGBoost中的二阶梯度

L(x+δx)≈L(x)+L′(x)δx+12L″(x)δx2L(x+ \delta x) \approx L(x) + L(x) \delta x + \frac{1}{2}L(x) \delta x^2

L(x+δx)=L(x)+L′(x)δx+12L″(x)δx2=L(x)−12L′(x)2L″(x)<L(x)L(x+ \delta x) = L(x) + L(x) \delta x + \frac{1}{2}L(x) \delta x^2= L(x) - \frac{1}{2} \frac{L(x) ^2}{L(x)} < L(x) ，其中 δx=−1∗L′(x)L″(x)\delta x = -1 * \frac{L(x)}{L(x)}

其实这个对应的就是牛顿提升树.

Newton提升树

(1) 初始化 f0(x)=argmincΣi=1NL(yi,c)f_0(x) = argmin_c \Sigma_{i=1}^N L(y_i,c)

(2) 对 m=1,2,...,Mm=1,2,...,M

(a) 对 i=1,2,...,Ni =1,2,...,N ,计算,<font color = red> rmi=−[∂L(yi,f(xi))∂f(xi)+12∂2L(yi,f(xi))∂f(xi)]f(x)=Fm−1(x)r_{mi} = - [\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} + \frac{1}{2}\frac{\partial _2L(y_i, f(x_i))}{\partial f(x_i)} ]_{f(x) = F_{m-1}(x) }

(b) 拟合残差 rmir_{mi} 学习一个回归树,得到 fm(x)f_m(x)

(c) 更新 Fm(x)=Fm−1(x)+fm(x)F_m(x) = F_{m-1}(x) + f_m(x)

(3) 得到回归问题提升树 FM(x)=Σi=1Mfi(x)F_M(x) = \Sigma_{i=1}^M f_i(x)

XGBoost中的正则项

传统的GBDT为了控制树的复杂度常常会对树的叶子个数加正则项进行控制, XGBoost不仅仅对于树中的叶子节点的个数进行控制,与此同时还对每个叶子节点的分数加入正则.即:

XGBoost的推导与算法构建

XGBoost的splitting准则的推导

下面我们对XGBoost中的一些公式进行推导,方便后续对于树的splitting有更好的理解.我们的目标依然不变,就是希望构建一棵新的树的时候,我们的损失函数尽可能的变得更小,即:

minΣk=1n(L(yk,y¯k+ft+1(xk))−L(yk,y¯k))min ~ \Sigma_{k=1}^n (L(y_k, \bar{y}_k+ f_{t+1}(x_{k})) - L(y_k, \bar{y}_k) ) ,其中 y¯k=Σj=1tfj(xk)$,$y¯k\bar{y}_k = \Sigma_{j=1}^{t}f_j(x_k)$, $\bar{y}_k 表示前 tt 棵树对于某个变量 xkx_k 的预测值.

使用二阶泰特展开并且去掉常数值,我们可以得到:

minΣk=1n(L(yk,y¯k+ft+1(xk))−L(yk,y¯k))≈minΣk=1n(gkft+1(xk)+12hkft+12(xk))+Ω(ft+1)min ~ \Sigma_{k=1}^n (L(y_k, \bar{y}_k+ f_{t+1}(x_k)) - L(y_k,\bar{y}_k) ) \approx min ~ \Sigma_{k=1}^n (g_k f_{t+1}(x_k) + \frac{1}{2}h_k f_{t+1}^2(x_k))+ \Omega (f_{t+1}) ,其中 gk=∂y¯kL(yk,y¯k),hk=∂y¯k2L(yk,y¯k)g_k = \partial_{\bar{y}_k} L(y_k, \bar{y}_k), h_k =\partial^2_{\bar{y}_k}L(y_k,\bar{y}_k) .

到这边已经差不多了,因为我们的模型是树模型,而树模型 fif_i 是由多个叶子节点 w1,w2,...,wTiw_1,w_2,...,w_{T_i} 组成.

令 Ij={i|q(xi)=j}I_j = \{i | q(x_i) = j \} 表示第 ii 个样本落入到了第 jj 个叶子节点中.则:

minΣk=1n(gkft+1(xk)+12hkft+12(xk))+Ω(ft+1)min ~ \Sigma_{k=1}^n (g_k f_{t+1}(x_k) + \frac{1}{2}h_k f_{t+1}^2(x_k))+ \Omega (f_{t+1})

minΣj=1Tt+1[(Σi∈Ijgi)wj+12(Σi∈Ijhi+λ)wj2]+γTt+1min \Sigma_{j=1}^{T_{t+1}} [(\Sigma_{i \in I_j} g_i) w_j + \frac{1}{2} (\Sigma_{i \in I_j}h_i + \lambda) w_j^2] + \gamma T_{t+1}

wj∗=−Σi∈IjgiΣi∈Ijhi+λw_j^* = - \frac{\Sigma_{i \in I_j} g_i}{\Sigma_{i \in I_j}h_i + \lambda}

对应的最优值就是: −12Σj=1Tt+1(Σi∈Ijgi)2Σi∈Ijhi+λ+γTt+1- \frac{1}{2} \Sigma_{j=1}^{T_{t+1}} \frac{(\Sigma_{i \in I_j }g_i)^2}{\Sigma_{i \in I_j}h_i + \lambda} + \gamma T_{t+1}

如果分割过后,我们左右子树的值的和相比于原先的值有增加并且大于某一个阈值,那么我们就寻找能获取最大值的分割点进行分割,反之我们就不进行分割. 即:

Lsplit=12[(Σi∈ILgi)2Σi∈ILhi+λ+(Σi∈IRgi)2Σi∈IRhi+λ−(Σi∈Igi)2Σi∈Ihi+λ]−γL_{split} = \frac{1}{2} [ \frac{(\Sigma_{i \in I_L} g_i)^2}{\Sigma_{i \in I_L} h_i + \lambda} + \frac{(\Sigma_{i \in I_R} g_i)^2}{\Sigma_{i \in I_R} h_i + \lambda} - \frac{(\Sigma_{i \in I} g_i)^2}{\Sigma_{i \in I} h_i + \lambda} ] - \gamma

XGBoost初始算法(Exact Greedy Algorithm)

XGBoost近似算法

当我们数据的规模足够大的时候，我们的数据较难存到内存中去,而且大量的数据使得计算量也变得很大,此时Exact Greedy的算法就不太实用,所以我们往往会寻求一种近似算法,而XGBoost的作者陈天奇针对该问题提出了一个新的近似算法,算法的核心可以参考XGBoot论文的"3.3 Weighted Quantile Sketch"部分.

Extreme部分

XGBoost的核心算法思想还是属于GBDT那一套,但此外,XGBoost还有着它的其他优势,正如陈天奇所述的,XGBoost中Extreme部分更多的是系统设计层面的,它是将我们的机器用到了极致.其中核心的包括:

具体的细节我就不再累述,可以参考陈天奇的论文以及他的代码进行细细的研究.

XGBoost的其他特性

XGBoost可以认为是一款集成了多种机器学习算法思想的一款利器:

参考资料

如果本篇文章对你有帮助，请留个赞再走哇~