CNN 可视化-热力图-数据可视化热力图分析怎么做

2023-08-10 21:42:41

0. 前言

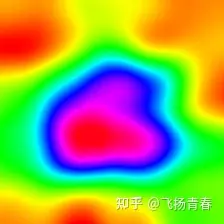
图1是原图;图2热力图,灰度越高证明温度越高;图3是对热力图做了伪彩处理;图4是热力图与原图做了blending之后的结果。

原图中有一只鸟，很多时候我们好奇，我们的神经网络为什么将这幅图判断为一只鸟，是图片的哪一部分对最终的决策影响最大？观察图4，该图告诉我们鸟类的翅膀处温度最高，即翅膀对最后结果的影响是最大的。

故热力图的作用：用来判断图像哪一部分对最终的结果影响最大。

图1

图2 热力图

图3 对热力图进行伪彩处理

图4 将伪彩处理的热力图与原图做blending

1.热力图原理简单介绍

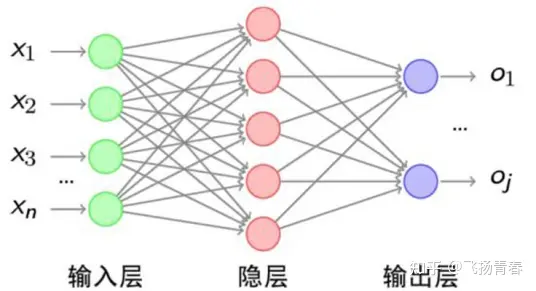
我们先以一个简单的MLP为例来说明，假设输入只有一张特征图。

如图5所示，图中的输入 $x$ x 是特征图p做了展平处理后得到的向量。其中 $xm$ x_{m} 对应像素 $pi,j$ p_{i,j} ,i为像素所在行，j为所在列，即m = i*clos+j。

我们已知 $O1=f(x1,x2,...,xn)$ O_{1} = f(x_{1},x_{2},...,x_{n}) ,所以我们知道增量 $ΔO1$ \Delta O_{1} 为

$ΔO1=\partialO1\partialx1*Δx1+\partialO1\partialx2*Δx2+...+\partialO1\partialxn*Δxn$ \Delta O_{1} =\frac{\partial O_{1}}{\partial x_{1}}*\Delta x_{1} + \frac{\partial O_{1}}{\partial x_{2}}*\Delta x_{2} + ... + \frac{\partial O_{1}}{\partial x_{n}}*\Delta x_{n}

可以认为第m个分量的增量 $Δxm$ \Delta x_{m} 对输出 $ΔO1$ \Delta O_{1}的贡献为 $\partialO1\partialxm*Δxm$ \frac{\partial O_{1}}{\partial x_{m}}*\Delta x_{m}

假设 $Δxm=xm$ \Delta x_{m} = x_{m} 则有

$ΔO1=\partialO1\partialx1*x1+\partialO1\partialx2*x2+...+\partialO1\partialxn*xn$ \Delta O_{1} =\frac{\partial O_{1}}{\partial x_{1}}*x_{1} + \frac{\partial O_{1}}{\partial x_{2}}*x_{2} + ... + \frac{\partial O_{1}}{\partial x_{n}}* x_{n}

故 $xm$ x_{m} 对 $O1$ O_{1} 的贡献为 $\partialO1\partialxm*xm$ \frac{\partial O_{1}}{\partial x_{m}}*x_{m} 。即像素 $pi,j$ p_{i,j} 的贡献为 $\partialO1\partialxm*xm$ \frac{\partial O_{1}}{\partial x_{m}}*x_{m} 。

故热力图点(i,j)处的灰度值为 $\partialO1\partialxm*xm$ \frac{\partial O_{1}}{\partial x_{m}}*x_{m} 。

根据前面的介绍我们知道，要想得到热力图，我们就需要知道两个内容：

1.特征图每个像素的灰度值 $xm$ x_{m}

2.输出相对于每个像素的梯度 $\partialO1\partialxm$ \frac{\partial O_{1}}{\partial x_{m}}

所以计算热力图时，选择不同的特征图，或选择不同的输出类都会对结果产生影响。

2. Lenet的热力图

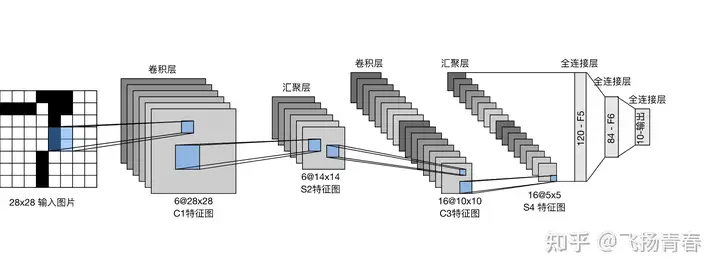
前面介绍了MLP的原理，但是一般来说我们很少用MLP，更多的是用卷积神经网络，那本节介绍Lenet的热力图实现。

可以看到Lenet最后三层即为MLP,故为了方便介绍，我们利用汇聚层的输出作为上一节中MLP的输入特征图，最后三层为上一节中的MLP。根据上图可知一共有16张特征图，每张特征图像素数为25，所以全连接层120-F5的输入为400维的向量x，且第h张特征图中的像素对应向量x中的元素为 $xh*25$ x_{h*25} ~ $x25*(h+1)$ x_{25*(h+1)} 。

不过这里有一处与上一节中不同，上一节中的向量x只有一个分量 $xm$ x_{m} 对应热力图中的 $pi,j$ p_{i,j} ，但是我们现在有16张特征图，所以 $pi,j$ p_{i,j} 在输入向量中共有16个值与之对应，分别为： $pi,j\Rightarrowxm+25*h,m=i*5+j,h=0,1,..,15$ p_{i,j} \Rightarrow x_{m+25*h},m = i*5+j,h=0,1,..,15 。

所以热力图 $pi,j$ p_{i,j} 处的值不再是 $\partialO1\partialxm*xm$ \frac{\partial O_{1}}{\partial x_{m}}*x_{m} ，而是 $\sumh=015\partialO1\partialxm+25*h*xm+25*h$ \sum_{h=0}^{15}{\frac{\partial O_{1}}{\partial x_{m+25*h}}*x_{m+25*h} } ，这样就得到了最终结果。

不过一般认为，同一张特征图内的所有像素相对于输出O1的梯度都是相同的，即如下各量相同。

$\partialO1\partialxm,m=h*25,...,(h*25+25)$ \frac{\partial O_{1}}{\partial x_{m}},m=h*25,...,(h*25+25) 。

所以用上述各量的均值 $wh=\summ=0m=25\partialO1\partialxm+25*h25$ w_{h} =\frac{\sum_{m=0}^{m=25}{\frac{\partial O_{1}}{\partial x_{m+25*h}}}}{25}来替代 $\partialO1\partialxm+25*h$ \frac{\partial O_{1}}{\partial x_{m+25*h}} 更为合适，所以有热力图 $pi,j$ p_{i,j}处的值为：

n $\sumh=015wh*xm+25*h$ \sum_{h=0}^{15}{w_{h}*x_{m+25*h} } 。

所以我们总结热力图所需为：

1.某一层的所有特征图

2.计算第h张特征图每个像素相对于输出O1的梯度，并求梯度均值得到权重wh

3.令 $\sumh=015wh*xm+25*h=\sumh=015wh*ph(i,j)$ \sum_{h=0}^{15}{w_{h}*x_{m+25*h} } = \sum_{h=0}^{15}{w_{h}*p_h(i,j) } 求的热力图像素(i,j)处的灰度值

3. 热力图步骤

下面以resnet-18为例来介绍具体的代码实现

热力图步骤如下：

0.设置网络，保存目标层的输出与其梯度到全局遍历self.target_layer,与self.gradients中，这样设置是因为pytorch默认不保留中间层的值与梯度。1.提取特征图与梯度图1.1 前向传播，计算出目标类的最终输出值model_output，以及目标层的特征图的输出conv_output。1.2 反向传播，获取目标类相对于目标层各特征图的梯度。1.2.1 清零梯度：model.zero_grad() 1.2.2 计算反向传播 :model_output.backward1.2.3 获取目标层各特征图的梯度 2.生成热力图2.1 对梯度图求均值，得到一个标量，作为权重2.2 用权重分别与对应的特征图相乘，然后将所有结果相加，得到热力图2.3 对热力图做后处理，是的热力图的灰度范围在（0，255）之间

步骤与代码的对应关系如下：

4.模型设置代码

代码如下，主要工作是：

0.设置网络，保存目标层的输出与其梯度

class CamExtractor(): """ Extracts cam features from the model """ def __init__(self, model, target_layer): self.model = model #用于储存模型 self.target_layer = target_layer#目标层的名称 self.gradients = None #最终的梯度图 def save_gradient(self, grad): self.gradients = grad #用于保存目标特征图的梯度（因为pytorch只保存输出，相对于输入层的梯度 #，中间隐藏层的梯度将会被丢弃，用来节省内存。如果想要保存中间梯度，必须 #使用register_hook配合对应的保存函数使用，这里这个函数就是对应的保存 #函数其含义是将梯度图保存到变量self.gradients中，关于register_hook #的使用方法我会在开一个专门的专题，这里不再详述 def forward_pass_on_convolutions(self, x): """ Does a forward pass on convolutions, hooks the function at given layer """ conv_output = None for name,layer in pretrained_model._modules.items(): if name == "fc": break x = layer(x) if name == self.target_layer: conv_output = x #将目标特征图保存到conv_output中 x.register_hook(self.save_gradient) #设置将目标特征图的梯度保存到self.gradients中 return conv_output, x #x为最后一层特征图的结果 def forward_pass(self, x): """ Does a full forward pass on the model """ # Forward pass on the convolutions conv_output, x = self.forward_pass_on_convolutions(x) x = x.view(x.size(0), -1) # Flatten # Forward pass on the classifier x = self.model.fc(x) return conv_output, x

如上代码代码块，函数forward_pass_on_convolutions(self, x):中的如下代码段最为关键分别对应步骤1.1，1.2

if name == self.target_layer: x.register_hook(self.save_gradient) #步骤1.2 设置将目标特征图的梯度保存到self.gradients中 conv_output = x #步骤1.1 将目标特征图保存到conv_output中

5.生成热力图

1.提取特征图与梯度图1.1 前向传播，计算出目标类的最终输出值model_output，以及目标层的特征图的输出conv_output。1.2 反向传播，获取目标类相对于目标层各特征图的梯度。1.2.1 清零梯度：model.zero_grad() 1.2.2 计算反向传播 :model_output.backward1.2.3 获取目标层各特征图的梯度 2.生成热力图2.1 对梯度图求均值，得到一个标量，作为权重2.2 用权重分别与对应的特征图相乘，然后将所有结果相加，得到热力图2.3 对热力图做后处理，是的热力图的灰度范围在（0，255）之间

class GradCam(): """ Produces class activation map """ def __init__(self, model, target_layer): self.model = model self.model.eval() # Define extractor self.extractor = CamExtractor(self.model, target_layer) #用于提取特征图与梯度图 def generate_cam(self, input_image, target_class=None): #1.1 前向传播，计算出目标类的最终输出值model_output，以及目标层的特征图的输出conv_output conv_output, model_output = self.extractor.forward_pass(input_image) if target_class is None: target_class = np.argmax(model_output.data.numpy()) #one hot编码，令目标类置1 one_hot_output = torch.FloatTensor(1, model_output.size()[-1]).zero_() one_hot_output[0][target_class] = 1 # 步骤1.2 反向传播，获取目标类相对于目标层各特征图的梯度 target = conv_output.data.numpy()[0] # 步骤1.2.1 清零梯度：model.zero_grad() self.model.zero_grad() # 步骤1.2.2 计算反向传播 model_output.backward(gradient=one_hot_output, retain_graph=True) # 步骤1.2.3 获取目标层各特征图的梯度 guided_gradients = self.extractor.gradients.data.numpy()[0] # 步骤2.1 对每张梯度图求均值，作为与其对应的特征图的权重 weights = np.mean(guided_gradients, axis=(1, 2)) # Take averages for each gradient # 初始化热力图 cam = np.ones(target.shape[1:], dtype=np.float32) # 步骤2.2 计算各特征图的加权值 for i, w in enumerate(weights): cam += w * target[i, :, :] #步骤2.3 对热力图进行后处理，即将结果变换到0~255 cam = np.maximum(cam, 0) cam = (cam - np.min(cam)) / (np.max(cam) - np.min(cam)) # Normalize between 0-1 cam = np.uint8(cam * 255) # Scale between 0-255 to visualize cam = np.uint8(Image.fromarray(cam).resize((input_image.shape[2], input_image.shape[3]), Image.ANTIALIAS))/255 return cam

以上就是关于《CNN 可视化-热力图-数据可视化热力图分析怎么做》的全部内容，本文网址：https://www.7ca.cn/baike/63134.shtml，如对您有帮助可以分享给好友，谢谢。

标签:

声明