S4-3 幂函数-幂函数的三种形式

 

前言

幂函数是我们最常见到的函数，与之相关的一次函数和二次函数也都是最基础的初等函数。

二次函数

先对二次函数做一个总结。

二次函数的一般式为：

f(x)=ax2+bx+c,a≠0f(x)=ax^2+bx+c,\quad a\neq 0

配方变形为顶点式则为：

f(x)=a(x−m)2+lf(x)=a(x-m)^2+l

利用两根写成两根式为：

f(x)=a(x−x1)(x−x2)f(x)=a(x-x_1)(x-x_2)

由两根式和一般式，比较系数可得韦达定理：

x1+x2=−ba,x1x2=cax_1 +x_2=\displaystyle -\frac{b}{a},x_1 x_2=\frac{c}{a}

二次函数的图像是抛物线，具有对称轴：

x=−b2ax=\displaystyle -\frac{b}{2a}

对称轴两侧函数具有单调性，由此可以求区间最值。

根据一般式，可以得到求根公式：

x=−b±b2−4ac2a\displaystyle x=\frac{-b\pm \sqrt{b^2 -4ac} }{2a}

根据其中的判别式：

Δ=b2−4ac\Delta =b^2-4ac

可以知道二次方程f(x)=0是否在实数域有解，从而可以知道二次函数的区间正负性。

所以对于一元二次不等式，可以通过移项将一边变成0后求解。

幂函数

接下来我们讨论幂函数，形式为：

f(x)=xa,a∈Rf(x)=x^a,\quad a\in \mathbb{R}

我们先来复习其基本定义，如果a是正整数，则很容易根据乘法计算幂。

如果是全体整数，根据幂的计算法则，也可以计算幂：

xax−a=x0=1⟺x−a=1xa\displaystyle x^a x^{-a}=x^0=1\iff x^{-a}=\frac{1}{x^a}

对于有理数，我们也根据幂的计算法则，规定有：

​ xp/q=xpq x^{p/q}=\sqrt[q]{x^p}

探索：无理数幂如何处理？

由此我们可以推导判断有理幂函数的各种性质。

幂函数的性质

先看一些常见的幂函数图像：

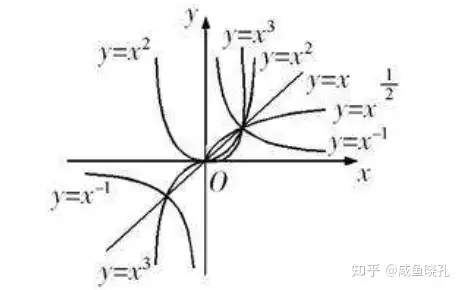
显然所有幂函数在第一象限都有定义，且过点(1,1)。

可以证明，幂函数在第四象限不存在任何图像。

练习：证明这个结论。

接着我们讨论单调性，只看第一象限，其他象限根据奇偶性可求。

如果a>0，其在第一象限单调递增。

如果a<0，其在第一象限单调递减，且x轴和y轴是两条渐近线。

下面讨论奇偶性，显然a是奇数则幂函数是奇函数，反之是偶函数。

而如果a是有理数，则分母为偶数时，幂函数定义域不对称，是非奇非偶函数。

分母为奇数时，不改变函数的奇偶性，和分子的奇偶性相同。

练习：证明这些结论。

探索：幂函数还有哪些性质？

多项式函数

这里再介绍一些简单的多项式函数知识。

实数域上的多项式，一定可以分解为一些一次多项式和二次多项式的乘积，由此可以求出n个复数域上的根。

且由此可知，最高次为奇数次的多项式函数一定有实根，也可以通过连续性得到这个结论。

探索：如何证明这些结论？

探索：多项式还有哪些性质？