常微分方程探索物种相互作用之谜：捕食者-被捕食者模型-常微分方程组的相图

 

探索自然界中物种相互作用的微分方程模型一直是生态学和数学领域的研究热点之一。而其中最经典且引人入胜的模型之一便是捕食者-被捕食者模型，也被称为predator-prey模型。这个模型以两个物种之间的相互关系为基础，既揭示了捕食者如何影响被捕食者数量的变化，也描述了被捕食者如何影响捕食者数量的变化。那么，如何利用微分方程解析或数值方法揭示这一错综复杂的相互作用呢？在本文中，我们将深入探讨捕食者-被捕食者模型并演示如何使用数值求解方法，以图表形式展示捕食者和被捕食者数量随时间的变化曲线。随着我们逐步深入，相信您对这一引人入胜的模型将产生浓厚兴趣，并加深对自然界物种相互作用的理解。

1.捕食者-被捕食者模型简介

捕食者-被捕食者模型描述了两个物种之间的相互作用，其中一个物种称为捕食者，另一个物种称为被捕食者。它们之间的数量变化受到多种因素的影响，如捕食行为、繁殖和自然死亡等。

这个模型的基本原则是：捕食者数量的增加会导致被捕食者数量的减少；而被捕食者数量的减少又会导致捕食者数量的减少。这种相互依赖的关系使得两个物种的数量呈现周期性波动。

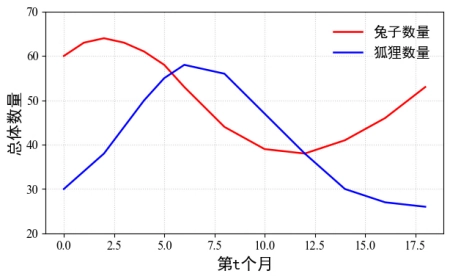
1.1捕食者-被捕食者模型的研究历程

捕食者-被捕食者模型是生态学和数学领域的经典模型之一。它的研究历程可以追溯到19世纪末，以下是对该模型的研究历程进行的概述：

1.1.1阿尔弗雷德洛特卡（Alfred J. Lotka）和弗朗茨冯里希特（Vito Volterra）

捕食者-被捕食者模型的最早形式可以追溯到20世纪初。阿尔弗雷德洛特卡和弗朗茨冯里希特分别独立提出了这个模型，并在他们的工作中描述了捕食者和被捕食者之间的数量关系。洛特卡使用微分方程推导了捕食者-被捕食者模型的基本公式。

1.1.2.罗伯特迪基斯勒（Robert May）

在20世纪70年代，罗伯特迪基斯勒对捕食者-被捕食者模型进行了深入研究，并提出了著名的“繁荣与灭亡”理论。他发现，捕食者和被捕食者数量之间的相互依赖关系可以导致模型的不稳定性，即周期性的数量波动或者灭绝。

1.1.3.本杰明吉诺森（Benjamin Ginzburg）

在20世纪90年代末和21世纪初，本杰明吉诺森的研究推动了对捕食者-被捕食者模型的进一步理解。他提出了“两通道”模型，通过考虑能源流动和信息反馈等因素，使模型更加贴近真实世界的生态系统。

《数学家的故事》带你探索数学巨人的精彩人生！揭秘数学的历史，了解这些伟大数学家创造里程碑式成果的故事。阿基米德用数学战胜罗马战舰，牛顿在干农活时沉迷于数学问题，欧拉巧思妙想帮爸爸扩大羊圈，高斯十岁时就能运用等差数列求和……《数学家的故事》带领我们徜徉在数学故事的长廊中，让我们从此爱上数学。

2.数学建模：微分方程

为了更好地理解捕食者-被捕食者模型，我们需要使用数学工具对其进行建模和求解。最常见的方法是使用微分方程。

在捕食者-被捕食者模型中，我们可以得到以下微分方程：

dx/dt = x - xy

dy/dt = xy - y

其中，x表示捕食者的数量，y表示被捕食者的数量，、、和是代表不同相互作用的参数。

通过求解这组微分方程，我们可以预测捕食者和被捕食者数量随时间的变化。

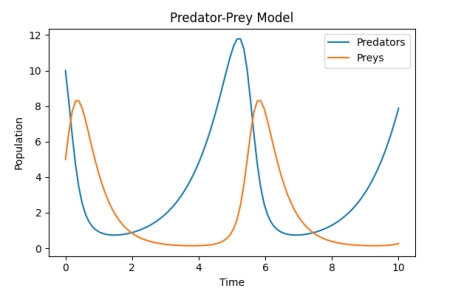
风靡数学爱好者的数学系列：《普林斯顿微积分读本》阐述了求解微积分的技巧，详细讲解了微积分基础、极限、连续、微分、导数的应用、积分、无穷级数、泰勒级数与幂级数等内容，旨在教会读者如何思考问题从而找到解题所需的知识点，着重训练大家自己解答问题的能力。

3.求解方法：数值与符号计算

要解决捕食者-被捕食者模型的微分方程，我们可以使用数值方法或符号计算。

3.1数值方法

数值方法通过将连续的时间变化离散化为一系列的时间步来近似求解微分方程。常见的数值方法包括欧拉法、龙格-库塔法等。

例如，我们可以使用欧拉法来求解：

x(i+1)= x(i)+ dt *( * x(i)- * x(i)* y(i))

y(i+1)= y(i)+ dt *( * x(i)* y(i)- * y(i))

其中，dt表示时间步长，i为时间步的索引。通过逐步迭代计算，我们可以得到捕食者和被捕食者数量随时间的数值解。数值方法的优点是易于实现，能够处理复杂的模型。然而，它们可能在精确性上存在一定程度的误差。

3.2符号计算

另一种方法是使用符号计算软件（如Mathematica、Maple等）进行解析求解。这些软件可以处理复杂的代数运算，得到精确的解析解或近似解。

符号计算的优点是能够提供精确的解析结果，有助于更深入地理解模型行为。然而，对于更复杂的模型，符号计算的计算量可能较大，求解过程可能会变得复杂。

4.实例演示：捕食者-被捕食者数量随时间的变化曲线

让我们以一个具体的实例来演示捕食者-被捕食者模型的数值求解过程，并绘制数量随时间的变化曲线。

在这个实例中，我们设定以下参数：

=0.2（捕食者自然增长率）

=0.1（捕食者对被捕食者的影响力）

=0.1（被捕食者繁殖速率）

=0.2（被捕食者自然死亡率）

初始条件为：

x(0)= 10（捕食者初始数量）

y(0)= 20（被捕食者初始数量）

通过数值求解方法（如欧拉法），我们可以得到捕食者和被捕食者数量随时间变化的数值解。将结果绘制成曲线图，可以清晰地观察到数量的周期性变化。欧拉法是一种数值近似方法，其精确度可能相对较低。如果需要更准确的结果，可以尝试使用其他数值求解方法（如四阶龙格-库塔法）。

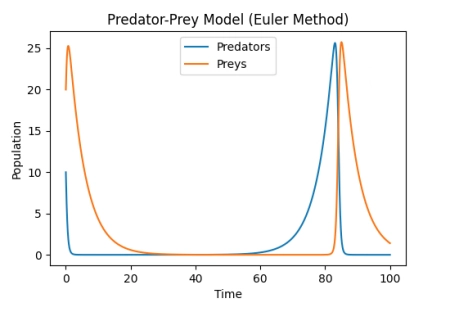
例如，在初始条件下，我们迭代计算了20个时间步（dt =0.1）后得到的结果如下所示：

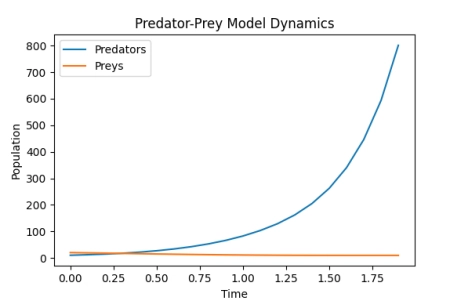
我们可以看到，捕食者和被捕食者的数量随着时间的推移呈现波动性变化。这种周期性变化由捕食者和被捕食者之间的相互作用所驱动。

结论

捕食者-被捕食者模型为我们理解物种相互作用、生态系统演化提供了重要的数学工具。通过数值求解或符号计算，我们可以预测捕食者和被捕食者数量的变化趋势。这一模型不仅在生态学领域有着广泛应用，还为生物多样性保护和害虫控制等问题提供了重要指导。

希望本篇文章对您理解捕食者-被捕食者模型有所帮助，并激发您对生态数学的兴趣！让我们一同探索自然界的奥秘，为构建更美好的未来贡献力量！

参考文献：

Murray, J. D.(2002).数学生物学I：介绍（第17卷）。斯普林格科学与商业媒体。Strogatz, S. H.(2014).非线性动力学与混沌：物理学、生物学、化学和工程应用。西景出版社。

想了解更多精彩内容，快来关注闻讯百通