高等数学系列R之四：傅立叶级数及变换（傅立叶级数推到）

 

2020-03-23

傅立叶级数是将周期函数表示成由多个 (或无穷多个) 不同频率的正弦函数和余弦函数的线性组合，这些不同的频率是不连续的，例如傅立叶级数：

f(x)=12+2π(sinx+13sin3x+15sin5x+⋯)f(x)=\frac{1}{2}+\frac{2}{π}(sinx+\frac{1}{3} sin3x+\frac{1}{5} sin5x+⋯) ，

其 sin 内的 x, 3x, 5x 是不连续的。而傅立叶积分是将傅立叶级数延伸到非周期函数，但这些不同的频率是连续的，例如：若 f(x) 的傅立叶积分=2π∫0∞cos⁡(wx)sin⁡(w)wdw\frac{2}{π} ∫_0^∞\frac{cos⁡(wx)sin⁡(w)}{w} dw ，其 cos 内的 wx 是连续的 (因 w 积分从 0 积到 ∞)。至于傅立叶变换是将函数变换成另一种形式，以方便某些领域的计算。接下来，我们将傅立叶级数及变换分成十个章节来探讨。

周期函数

(1). 若函数 f(x) 的定义域为实数集合 R 且存在一正数 T，使得 f(x+T)=f(x)，x∈R，则称 f(x) 为周期函数，且此正的数值 T 称为 f(x) 的周期。

(2). 若 f(x) 和 g(x) 的周期均为 T，则 h(x)=af(x)±bg(x) 亦为周期 T 的函数。

(3). 若 f(x) 的周期为 T，则 f(kx) 的周期为： Tk\frac{T}{k}。

(4). 若 f(x) 的周期为 mT，g(x) 的周期为 nT，则 h(x)=af(x)±bg(x) 的周期为 m, n 的最小公倍数乘以 T。(若 m, n 为分数，则先通分后再取分子的最小公倍数)

(5). 常数函数 f(x)=c，亦为周期函数，其周期为任意数。

(6). 级数 a0+a1cosx+b1sinx+a2cos2x+b2sin2x+…=a0+∑n=1∞(ancosnx+bnsinnx)a_0+a_1cosx+b_1sinx+a_2cos2x+b_2sin2x+…=a_0+\sum_{n=1}^\infty (a_ncosnx+b_nsinnx)

，其中 a0,a1,b1,a2,b2,… a_0, a_1, b_1, a_2, b_2, … 均为常数，则此级数称为三角级数，而 ai,bia_i, b_i 称为此级数的系数。

(7). 三角级数的周期为 2π。

(ex.47) 求 sin(2x)+cos(3x) 的周期。

Sol：

(1) . sin(2x) 的周期为 2π2=π\frac{2π}{2}=π

(2) . cos(3x) 的周期为 2π3\frac{2π}{3}，而 π=3π3π=\frac{3π}{3}，两周期的分子 3 和 2 的最小公倍数是 6，所以 sin(2x)+cos(3x) 的周期为 6π3=2π\frac{6π}{3}=2π

周期为 2π 的傅立叶级数

(1). 若函数 f(x) 是周期为 2π 的周期函数，则其可以用下面的三角级数表示： f(x)=a0+∑n=1∞(ancosnx+bnsinnx)f(x)=a_0+\sum_{n=1}^\infty (a_ncosnx+b_nsinnx)

(2). 在上式中，若 f(x) 已知，则 a0,an,bna_0, a_n, b_n 可由下法求得： a0=12π∫−ππf(x)dxa_0=\frac{1}{2π} \int_{-π}^{π}f(x)dx

an=1π∫−ππf(x)∙cosnxdxa_n=\frac{1}{π} \int_{-π}^{π}f(x)∙cosnxdx，n=1, 2, 3…

bn=1π∫−ππf(x)∙sinnxdxb_n=\frac{1}{π} \int_{-π}^{π}f(x)∙sinnxdx，n=1, 2, 3…

pf：略

(3). 用法：要求周期为 2π 的周期函数 f(x) 的傅立叶级数时，

(a). 抄下 f(x)=a0+∑n=1∞(ancosnx+bnsinnx)f(x)=a_0+\sum_{n=1}^\infty (a_ncosnx+b_nsinnx) 。

(b). 抄下 a0=12π∫−ππf(x)dxa_0=\frac{1}{2π} \int_{-π}^{π}f(x)dx。

(c). 将题目的 f(x) 代入 (b) 式。

(d). 将 (b) 式积分出来，求出 a0a_0 。

(e). 重复 (b)~(d) 式，算出 、an、bna_n、b_n 。

(f). 最后将 a0,an,bna_0, a_n, b_n 代入 (a) 式。

(g). an,bna_n, b_n 求出前三项之值 (n=1, 2, 3 代入)，找出其规律。

(4). 若 f(x)=a0+∑n=1∞(ancosnx+bnsinnx)f(x)=a_0+\sum_{n=1}^\infty (a_ncosnx+b_nsinnx) ，则右式称为 f(x) 的傅立叶级数，而a0,an,bna_0, a_n, b_n 称为 f(x) 的傅立叶系数。

(ex.48) 求 f(x) 的周期为 2π，且 当当f(t)={0,当−π<t<01,当0<x<πf(t)=\begin{cases} 0,当-π<t<0\\[2ex] 1,当0<x<π\\[2ex] \end{cases} ，求 f(x) 的傅立叶级数。

Sol：由傅立叶级数公式知

(1). f(x)=a0+∑n=1∞(ancosnx+bnsinnx)f(x)=a_0+\sum_{n=1}^\infty (a_ncosnx+b_nsinnx)

(2). a0=12π∫−ππf(x)dx=12π∫−π00∙dx+∫0π1∙dx=12a_0=\frac{1}{2π}\int_{-π}^{π}f(x)dx=\frac{1}{2π}\int_{-π}^{0}0∙dx+\int_{0}^{π}1∙dx=\frac{1}{2}

(3). an=1π∫−ππcosnxdx=1π(∫−π00∙cosnxdx+∫0π1∙cosnxdx)=1nπ[sinnx|π0]=1nπ[sinnπ−sin0]=0a_n=\frac{1}{π}\int_{-π}^{π}cosnxdx=\frac{1}{π}(\int_{-π}^{0}0∙cosnxdx+\int_{0}^{π}1∙cosnxdx)=\frac{1}{nπ} [sinnx|\begin{matrix} π\\0\\ \end{matrix}]=\frac{1}{nπ} [sinnπ-sin0]=0

偶函数与奇函数的傅立叶级数

此节的目的是要简化计算傅立叶系数的过程。

(1). 若函数 f(x) 满足 f(-x)=f(x)，则 f(x) 称为偶函数，例如： x2,cos(x)x^2, cos(x) 等，或图形沿 y 轴对折，左右两边图形会重叠在一起，如下图：

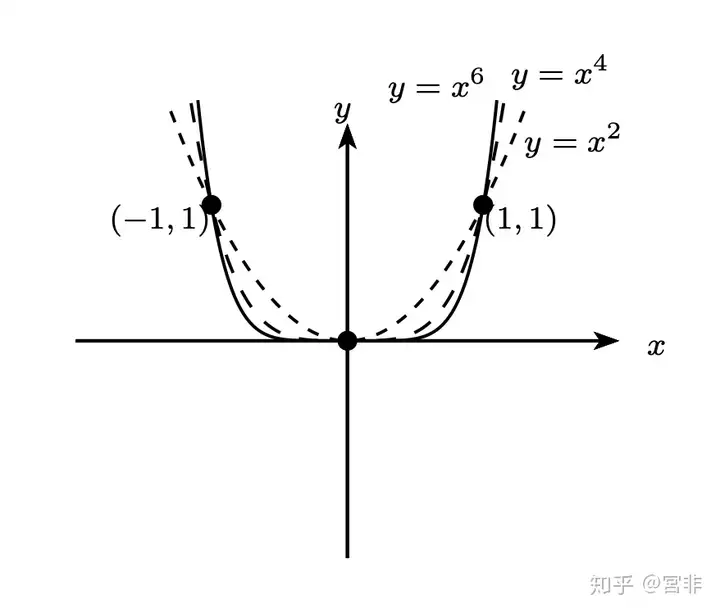
(2). 若函数 g(x) 满足 g(-x)=-g(x)，则 g(x) 称为奇函数，例如： x3,sin(x)x^3, sin(x) 等，或图形沿 y 轴对折，再沿 x 轴对折，右上图形与左下图形会重叠在一起，如下图：

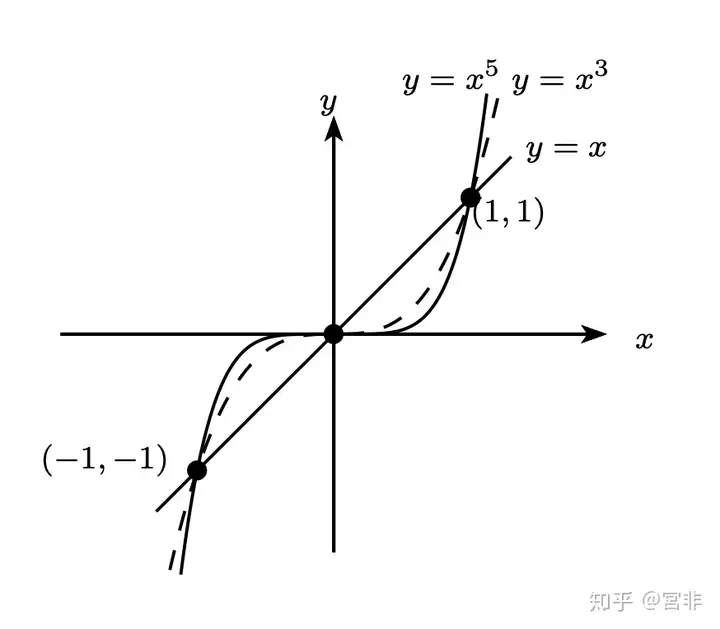
(3). 偶函数与偶函数的乘积为偶函数，例如： ・x2・x4=x6x^2・x^4=x^6 为偶函数；偶函数与奇函数的乘积为奇函数，例如： ・x2・x1=x3x^2・x^1=x^3 为奇函数；奇函数与奇函数的乘积为偶函数，例如： ・x1・x3=x4x^1・x^3=x^4 为偶函数。

(4). 偶函数积分积一个周期等于积半个周期的 2 倍，即若函数 f(x) 是周期为 2π 的偶函数，

∫−ππf(x)dx=2∫0πf(x)dx\int_{-π}^{π}f(x)dx=2\int_{0}^{π}f(x)dx 。

(5). 奇函数积分积一个周期的值为 0，即若函数 g(x) 是周期为 2π 的奇函数，则 ∫−ππg(x)dx=0\int_{-π}^{π}g(x)dx=0 。

(6). 若函数 f(x) 是周期为 2π 的周期函数，且为偶函数，则 f(x) 和 f(x)cosnx 为偶函数，f(x)sinnx 为奇函数，所以 f(x) 的傅立叶级数为： f(x)=a0+∑n=1∞(ancosnx)f(x)=a_0+\sum_{n=1}^\infty (a_ncosnx) ，

其中， a0=12π∫−ππf(x)dx=1π∫0πf(x)dxa_0=\frac{1}{2π}\int_ {-π}^{π}f(x)dx=\frac{1}{π}\int_{0}^{π}f(x)dx ， ⇒a0=1π∫−ππf(x)∙cosnxdx=2π∫0πf(x)∙cosnxdx⇒ a_0=\frac{1}{π}\int_{-π}^{π}f(x)∙cosnxdx=\frac{2}{π}\int_{0}^{π}f(x)∙cosnxdx ，，n=1,2,3,…，bn=0n=1, 2, 3,…，b_n=0 。

(7). 若函数 f(x) 是周期为 2π 的周期函数，且为奇函数，则 f(x) 和 f(x)cosnx 为奇函数，f(x)sinnx 为偶函数，所以 f(x) 的傅立叶级数为： f(x)=∑n=1∞bnsinnxf(x)=\sum_{n=1}^\infty b_nsinnx，

其中， b0=1π∫−ππf(x)∙sinnxdx=2π∫0πf(x)∙sinnxdx b_0=\frac{1}{π}\ ∫_{-π}^{π}f(x)∙sinnxdx=\frac{2}{π} ∫_0^πf(x)∙sinnxdx， ，n=1,2,3,…，a0=0,an=0n=1, 2, 3,…，a_0=0, a_n=0

(ex.49) f(x) 的周期为 2π，且 当当f(t)={1,当−π2<x<π20,当π2<x<3π2f(t)=\begin{cases} 1,当-\frac{π}{2}<x<\frac{π}{2}\\[2ex] 0,当\frac{π}{2}<x<\frac{3π}{2}\\[2ex] \end{cases} ，求 f(x) 的傅立叶级数。

Sol：f(x) 可改写成 当当当f(t)={0,当−π<x<−π21,当−−π2<x<π20,当π2<x<πf(t)=\begin{cases} 0,当-π<x<\frac{-π}{2}\\[2ex] 1,当-\frac{-π}{2}<x<\frac{π}{2}\\[2ex] 0,当\frac{π}{2}<x<π\\[2ex] \end{cases}

因为它是偶函数，所以

(1). f(x)=a0+∑n=1∞(ancosnx)f(x)=a_0+\sum_{n=1}^\infty(a_ncosnx)

(2). a0=1π∫−ππf(x)dx=1π[∫0π21dx+∫π2π0dx]=1π∙(π2−0)=12a_0=\frac{1}{π} ∫_{-π}^{π}f(x)dx=\frac{1}{π}[∫_{0}^{\frac{π}{2}}1dx+∫_{\frac{π}{2}}^π0dx]=\frac{1}{π}∙(\frac{π}{2}-0)=\frac{1}{2}

(3). a0=2π∫0πf(x)∙cosnxdx=2π[∫0π21∙cosnxdx+∫π2π0∙cosnxdx]=2π∙1nsinnx|π20=2nπsinnπ2a_0=\frac{2}{π} ∫_{0}^{π}f(x)∙cos nxdx=\frac{2}{π} [∫_{0}^{\frac{π}{2}}1∙cosnxdx+∫_{\frac{π}{2}}^π0∙cosnxdx]=\frac{2}{π}∙\frac{1}{n} sinnx|\begin{matrix} \frac{π}{2}\\0\\ \end{matrix}=\frac{2}{nπ} sin \frac{nπ}{2}

(4). f(x)=a0+∑n=1∞ancosnx=12+∑n=1∞2nπsin⁡(nπ2)∙cos⁡(nx)=12+2π∙cosx−23π∙cos3x+25π∙cos5x+…f(x)=a_0+\sum_{n=1}^\infty a_ncos nx=\frac{1}{2}+\sum_{n=1}^\infty \frac{2}{nπ} sin⁡(\frac{nπ}{2})∙cos⁡(nx)=\frac{1}{2}+\frac{2}{π}∙cosx-\frac{2}{3π}∙cos3x+\frac{2}{5π}∙cos5x+…

任意周期函数之傅立叶级数

(1). 周期为 2L 的周期函数 f(t) (注：L 为半周期)，其傅立叶级数为：

f(x)=a0+∑n=1∞[ancos(n∙πLx)+bnsin(n∙πLx)]f(x)=a_0+\sum_{n=1}^\infty [a_ncos(n∙\frac{π}{L} x)+b_nsin(n∙\frac{π}{L} x)] ，其中，

a0=12L∫−LLf(x)dxa_0=\frac{1}{2L} ∫_{-L}^{L}f(x)dx ， an=1L∫−LLf(x)cos⁡(n∙πLx)dxa_n=\frac{1}{L} ∫_{-L}^{L}f(x)cos⁡(n∙\frac{π}{L} x)dx ， bn=1L∫−LLf(x)sin⁡(n∙πLx)dxb_n=\frac{1}{L} ∫_{-L}^{L}f(x)sin⁡(n∙\frac{π}{L} x)dx

Pf：略

说明：周期为 2L 的傅立叶级数，只要将周期为 2π 的傅立叶级数作下列二项修改，

(a). 将公式的所有 π 改成 L；

(b). 将 sin 和 cos 内的 x 改成 πL∙x\frac{π}{L}∙x 。

(2). 周期为 2L 的偶函数 f(x)，其傅立叶级数为： f(x)=a0+∑n=1∞ancos(n∙πLx)f(x)=a_0+\sum_{n=1}^\infty a_ncos(n∙\frac{π}{L} x) ，

其中， a0=12L∫−LLf(x)dxa_0=\frac{1}{2L} ∫_{-L}^{L}f(x)dx ， an=2L∫−LLf(x)cos⁡(n∙πLx)dxa_n=\frac{2}{L} ∫_{-L}^{L}f(x)cos⁡(n∙\frac{π}{L} x)dx 。

(3). 周期为 2L 的奇函数 f(x)，其傅立叶级数为： f(x)=∑n=1∞bnsin(n∙πLx)f(x)=\sum_{n=1}^\infty b_nsin(n∙\frac{π}{L} x) ，

其中， bn=2L∫0Lf(x)sinnπxLdxb_n=\frac{2}{L} ∫_{0}^{L}f(x)sin \frac{nπx}{L} dx 。

(ex.50) 周期为 4 的 f(x)，且 当当f(t)={0,当−2<t<01,当0<t<2f(t)=\begin{cases} 0,当-2<t<0\\[2ex] 1,当0<t<2\\[2ex] \end{cases} ，求 f(x) 的傅立叶级数。

Sol：週期 2L=4 ⇒L=2⇒L=2 ，所以

(1). f(t)=a0+∑n=1∞[ancos(n∙πLt)+bnsin(n∙πLt)f(t)=a_0+\sum_{n=1}^\infty [a_ncos(n∙\frac{π}L t)+b_nsin(n∙\frac{π}{L} t)

(2). a0=12L∫−LLf(t)dt=14∫021∙dt=12a_0=\frac{1}{2L} ∫_{-L}^{L}f(t)dt=\frac{1}{4} ∫_{0}^{2}1∙dt=\frac{1}{2}

(3). an=1L∫−LLf(t)cos∙nπLtdt=12∫02cosnπ2tdt=12∙2nπ∙sin⁡(nπt2)|20=1nπ[sinnπ−sin0]=0a_n=\frac{1}{L} ∫_{-L}^{L}f(t)cos∙\frac{nπ}{L} tdt=\frac{1}{2} ∫_{0}^{2}cos \frac{nπ}{2} tdt=\frac{1}{2}∙\frac{2}{nπ}∙sin⁡(\frac{nπt}{2})|\begin{matrix} 2\\0\\ \end{matrix}=\frac{1}{nπ} [sinnπ-sin0]=0

(4). bn=1L∫−LLf(t)sin∙nπLtdt=12∫02sinnπ2tdt=12∙(−2nπcos⁡(nπt2)|20=1nπ[1−cosnπ]=b_n=\frac{1}{L} ∫_{-L}^{L}f(t)sin∙\frac{nπ}{L} tdt=\frac{1}{2} ∫_{0}^{2}sin\frac{nπ}{2} tdt=\frac{1}{2}∙(-\frac{2}{nπ}cos⁡(\frac{nπt}{2})|\begin{matrix} 2\\0\\ \end{matrix}=\frac{1}{nπ} [1-cosnπ]=

f(t)={2nπ,n=1,3,5...0,n=2,4,6...f(t)=\begin{cases} \frac{2}{nπ},n=1, 3, 5...\\[2ex] 0,n=2, 4, 6...\\[2ex] \end{cases}

(5). 所以 f(t)=a0+∑n=1∞[ancos(n∙πLt)+bnsin(n∙πLt)]=12+∑n=1∞[1nπ(1−cosnπ)(sin⁡(nπ2t)]f(t)=a_0+\sum_{n=1}^\infty [a_ncos(n∙\frac{π}{L} t)+b_nsin(n∙\frac{π}{L} t)]=\frac{1}{2}+\sum_{n=1}^\infty [\frac{1}{nπ} (1-cosnπ)(sin⁡(\frac{nπ}{2} t)]

=12+2π(sinπ2t+13sin3π2t+⋯)=\frac{1}{2}+\frac{2}{π}(sin\frac{π}{2} t+\frac{1}{3} sin \frac{3π}{2} t+⋯)

半周期函数 (或称半周期展开)

(1). 若給定一半週期函數，如週期是 2L 的函數，f(x) 只在 [0, L] 內有定義，現要將函數f(x)的定義擴展到 (-∞, ∞)，其擴展的方式有二種：

(a). 偶函数扩展：即先扩展到 [-L, L] 一周期的偶函数，再扩展到 (-∞, ∞)。

(b). 奇函数扩展：即先扩展到 [-L, L] 一周期的偶函数，再扩展到 (-∞, ∞)。

函数本来定义在 [0, L] 半周期内，经以上的扩展方式，周期均变为 2L，称为"半周期展开"。

(2). 要求半周期展开的傅立叶级数时，可以使用上节「任意周期函数之傅立叶级数」方法求得，及若是偶函数扩展或奇函数扩展，则代偶函数或奇函数的傅立叶级数公式。

(ex.51) 求下列函数的偶函数和奇函数半周期展开，且 当当f(t)={1,当0<x<230,当23<x<2f(t)=\begin{cases} 1,当0<x<\frac{2}{3}\\[2ex] 0,当\frac{2}{3}<x<2\\[2ex] \end{cases} 。

Sol：半周期 L=2

(1). 展开成一周期偶函数

(a). 偶函数扩展： f(x)=a0+∑n=1∞ancos(nπLx)f(x)=a_0+\sum_{n=1}^\infty a_ncos(\frac{nπ}{L} x)

(b). a0=1L∫0Lf(x)dt=12∫0231∙dx=13a_0=\frac{1}{L} ∫_{0}^{L}f(x)dt=\frac{1}{2} ∫_{0}^{\frac{2}{3}}1∙dx=\frac{1}{3}

(c). an=2L∫0Lf(x)cos∙nπxLdx=22∫0231∙cosnπx2dx=2nπsin⁡(nπ3)a_n=\frac{2}{L} ∫_{0}^{L}f(x)cos∙\frac{nπx}{L} dx=\frac{2}{2} ∫_{0}^{\frac{2}{3}}1∙cos \frac{nπx}{2} dx=\frac{2}{nπ} sin⁡(\frac{nπ}{3})

(d). n=1, 2, 3, …代入，得 a1=2πsin⁡(π3)=3πa_1=\frac{2}{π} sin⁡(\frac{π}{3})=\sqrt{\frac{3}{π}} 、 a2=22πsin⁡(2π3)=32πa_2=\frac{2}{2π} sin⁡(\frac{2π}{3})=\sqrt{\frac{3}{2π}} 、 a3=23πsin⁡(3π3)=0a_3=\frac{2}{3π} sin⁡(\frac{3π}{3})=0 、 a4=24πsin⁡(4π3)=−34πa_4=\frac{2}{4π} sin⁡(\frac{4π}{3})=-\sqrt{\frac{3}{4π}} 、 a5=25πsin⁡(5π3)=−35πa_5=\frac{2}{5π} sin⁡(\frac{5π}{3})=-\sqrt{\frac{3}{5π}} 、 aˊ=26πsin⁡(6π3)=0a_ˊ=\frac{2}{6π} sin⁡(\frac{6π}{3})=0 ，….

(e). 所以 f(x)=a0+∑n=1∞ancos(n∙πLx)=13+∑n=1∞(2nπsin⁡(nπ3)(cos⁡(nπx2))f(x)=a_0+\sum_{n=1}^\infty a_ncos(n∙\frac{π}{L} x) =\frac{1}{3}+\sum_{n=1}^\infty (\frac{2}{nπ} sin⁡(\frac{nπ}{3})(cos⁡(\frac{nπx}{2}))

=13+√3/πcos⁡(πx2)+32πcos(2πx2)−34πcos(4πx2)−35πcos(5πx2)+⋯=\frac{1}{3}+√3/π cos⁡(\frac{πx}{2})+\frac{\sqrt{3}}{2π} cos(\frac{2πx}{2})-\frac{\sqrt{3}}{4π} cos(\frac{4πx}{2})-\frac{\sqrt{3}}{5π} cos(\frac{5πx}{2})+⋯

(2). 展开成一周期奇函数

(a). 奇函数扩展： f(x)=∑n=1∞bncos(nπLx)f(x)=\sum_{n=1}^\infty b_ncos(\frac{nπ}{L} x)

(b). bn=2L∫0Lf(x)sin∙nπxLdx=22∫0231∙sinnπx2dx=−2nπ[cos⁡(nπ3−1)]b_n=\frac{2}{L} ∫_{0}^{L}f(x)sin∙\frac{nπx}{L} dx=\frac{2}{2} ∫_{0}^{\frac{2}{3}} 1∙sin \frac{nπx}{2} dx=-\frac{2}{nπ}[cos⁡(\frac{nπ}{3}-1)]

(c). n=1, 2, 3, …代入，得 b1=−2π[cos⁡(π3)−1]=1πb_1=-\frac{2}{π} [cos⁡(\frac{π}{3})-1]=\frac{1}{π} 、 b2=−22π[cos⁡(2π3)−1]=32πb_2=-\frac{2}{2π} [cos⁡(\frac{2π}{3})-1]=\frac{3}{2π} 、 b3=−23π[cos⁡(3π3)−1]=43πb_3=-\frac{2}{3π} [cos⁡(\frac{3π}{3})-1]=\frac{4}{3π} 、 b4=−24π[cos⁡(4π3)−1]=34πb_4=-\frac{2}{4π} [cos⁡(\frac{4π}{3})-1]=\frac{3}{4π} 、 b5=−25π[cos⁡(5π3)−1]=15πb_5=-\frac{2}{5π} [cos⁡(\frac{5π}{3})-1]=\frac{1}{5π} 、 b6=−26π[cos⁡(6π3)−1]=0b_6=-\frac{2}{6π} [cos⁡(\frac{6π}{3})-1]=0 ，….

(d). 所以 f(x)=∑n=1∞bncos(nπLx)=∑n=1∞[−2nπ(cos(nπ3)−1)(sin⁡(nπx2)]=f(x)=\sum_{n=1}^\infty b_ncos(\frac{nπ}{L} x) =\sum_{n=1}^\infty [-\frac{2}{nπ} (cos(\frac{nπ}{3})-1)(sin⁡(\frac{nπx}{2})]=

1πsin⁡(πx2)+32πsin(2πx2)+34πsin(4πx2)+15πsin(5πx2)+⋯\frac{1}{π} sin⁡(\frac{πx}{2})+\frac{3}{2π} sin(\frac{2πx}{2})+\frac{3}{4π} sin(\frac{4πx}{2})+\frac{1}{5π} sin(\frac{5πx}{2})+⋯

复数傅立叶级数

(1). 也可以用复数方法来求傅立叶级数，其与用前面的方法求出来的答案相同。

(2). 函数 f(x) 是周期为 2π 的函数，其复数傅立叶级数为 f(x)=∑−∞∞cneinxf(x)=\sum_{-∞}^\infty c_ne^{inx}

，其中， cn=12π∫−ππf(x)e−inxdxc_n=\frac{1}{2π} ∫_{-π}^{π}f(x)e^{-inx}dx ，n=0, ±1, ±2, …

(3). 要求复数傅立叶级数时，

(a). 抄下 f(x)=∑−∞∞cneinxf(x)=\sum_{-∞}^\infty c_ne^{inx} 。

(b). 抄下 cn=12π∫−ππf(x)e−inxdxc_n=\frac{1}{2π} ∫_{-π}^{π}f(x)e^{-inx}dx 。

(c). 将题目的 f(x) 代入 (b) 式。

(d). 将 (b) 式积分出来。

(e). 求出 f(x)=∑−∞∞cneinxf(x)=\sum_{-∞}^\infty c_ne^{inx} 中的第 -k 项 (即 c−kei(−k)xc_{-k}e^{i(-k)x} 和第 k 项 (即 ckei(k)xc_ke^{i(k)x} ，再将此二项相加起来，以消去虚数部分。

(f). 求出 f(x)=∑−∞∞cneinxf(x)=\sum_{-∞}^\infty c_ne^{inx} 的第 0 项 (即 c0ei(0)x=c0c_0e^{i(0)x}= c_0 )。

(g). f(x)=∑−∞∞cneinx==c0+∑−∞∞[c−kei(−k)x+ckeikx]f(x)=\sum_{-∞}^\infty c_ne^{inx} ==c_0+\sum_{-∞}^\infty[c_{-k}e^{i(-k)x} +c_ke^{ikx}] ，答案与用前面方法求出答案相同。

注：

(i). 若题目要求「复数傅立叶级数」，只要做到 (d) 步骤，再将 cnc_n 代回 (a) 式即可；

(ii). 若题目要求「傅立叶级数」，则还要往下做以消去虚数 i，其結果与用前面方法求出答案相同。

(4). 函数 f(x) 是周期为 2L 的函数，其复数傅立叶级数为： f(x)=∑−∞∞cneinπxLf(x)=\sum_{-∞}^\infty c_ne^\frac{inπx}{L}

，其中， cn=12L∫−LLf(x)e−inπxLdxc_n=\frac{1}{2L} ∫_{-L}^{L}f(x)e^\frac{-inπx}{L} dx ，n=0, ±1, ±2, …

说明：周期为 2L 的复数傅立叶级数只要将周期为 2π 的复数傅立叶级数作下列二项修改：

(a). 将公式的所有 π 改成 L；

(b). 将 e 的指数 x 改成 πxL\frac{πx}{L} 。

(ex.52) 若 f(x) 的周期为 2π，且 当当f(t)={1,当−π<x<00,当0<x<πf(t)=\begin{cases} 1,当-π<x<0\\[2ex] 0,当0<x<π\\[2ex] \end{cases} ，用复数方法求 f(x) 的傅立叶级数。

Sol：

(1). f(x)=∑−∞∞cneinxf(x)=\sum_{-∞}^\infty c_ne^{inx} 。

(2). cn=12π∫−ππf(x)e−inxdx=12π[∫−π00∙e−inxdx+∫0π1∙e−inxdx]=12π∙e−inx−in|π0=c_n=\frac{1}{2π} ∫_{-π}^{π}f(x)e^{-inx}dx=\frac{1}{2π} [∫_{-π}^{0}0∙e^{-inx} dx+∫_0^π1∙e^{-inx}dx]=\frac{1}{2π}∙\frac{e^{-inx}}{-in}|\begin{matrix} π\\0\\ \end{matrix}=

−12nπi(e−inx−1)=12nπi[cos⁡(−nπ)+isin(−nπ)−1]=12nπ[cos⁡(nπ)−1]\frac{-1}{2nπi} (e^{-inx}-1)=\frac{1}{2nπi}[cos⁡(-nπ)+isin(-nπ)-1]=\frac{1}{2nπ}[cos⁡(nπ)-1] 。

(注： eiθ=cosθ+isinθe^{iθ}=cosθ+isinθ ，因 n 是整数，所以 sin(-nπ)=0)

(3). (a). n=-k 代入 ⇒c−kei(−k)x=i2(−k)π[cos(−kπ)−1][cos⁡(−kx)+isin(−kx)]=⇒c_{-k}e^{i(-k)x}=\frac{i}{2(-k)π} [cos(-kπ)-1][cos⁡(-kx)+isin(-kx)]=

−i2kπ[cos⁡(kπ)−1][cos⁡(kx)−isin(kx)]=12kπ[cos⁡(kπ)−1][−sin⁡(kx)−icos(kx)]\frac{-i}{2kπ} [cos⁡(kπ)-1][cos⁡(kx)-isin(kx)]=\frac{1}{2kπ} [cos⁡(kπ)-1][-sin⁡(kx)-icos(kx)]

(b). n=k 代入 ⇒ckei(k)x=i2(−k)π[cos(kπ)−1][cos⁡(kx)+isin(kx)]=⇒c_{k}e^{i(k)x}=\frac{i}{2(-k)π} [cos(kπ)-1][cos⁡(kx)+isin(kx)]=

12kπ[cos⁡(kπ)−1][−sin⁡(kx)+icos(kx)]=12kπ[cos⁡(kπ)−1][−sin⁡(kx)+icos(kx)]\frac{1}{2kπ} [cos⁡(kπ)-1][-sin⁡(kx)+icos(kx)]=\frac{1}{2kπ} [cos⁡(kπ)-1][-sin⁡(kx)+icos(kx)]

(c). (a)+(b) ⇒c−keI(−k)x+ckeI(k)x=12kπ[cos(kπ)−1][−2isin(kx)]=1kπ[1−cos⁡(kπ)]sinkx⇒c_{-k}e^{I(-k)x}+c_{k}e^{I(k)x}=\frac{1}{2kπ} [cos(kπ)-1][-2isin(kx)]=\frac{1}{kπ} [1-cos⁡(kπ)]sinkx

(4). n=0 代入 c0=12π∫−ππf(x)e−inxdx|n=0=12π[∫−π00∙e−i0xdx+∫0π1∙e−i0xdx]=12c_0 =\frac{1}{2π} ∫_{-π}^{π} f(x) e^{-inx} dx|\begin{matrix} \\n=0\\ \end{matrix}=\frac{1}{2π}[∫_{-π}^{0} 0∙e^{-i0x} dx+∫_{0}^{π} 1∙e^{-i0x} dx]=\frac{1}{2}

(5). f(x)=∑n=−∞∞cneinx=c0+∑n=1∞[c−kei(−k)x+ckei(k)x]=12+∑n=1∞1nπ[1−cos(nπ)]sinnxf(x)=\sum_{n=-∞}^\infty c_ne^{inx} =c_0+\sum_{n=1}^\infty [c_{-k}e^{i(-k)x}+ c_ke^{i(k)x}]=\frac{1}{2}+\sum_{n=1}^\infty \frac{1}{nπ}[1-cos(nπ)]sinnx

(答案与「周期为 2π 的傅立叶级数」中 (ex.48) 相同。)

傅立叶积分

(1). 若函数 f(x) 为非周期性函数或考虑整个 x 轴时，就要使用傅立叶积分。

(2). f(x) 的傅立叶积分为： f(x)=∫0∞[A(w)cos⁡(wx)+B(w)sin⁡(wx)]dwf(x)=∫_{0}^{∞}[A(w) cos⁡(wx)+B(w)sin⁡(wx)]dw ，其中， A(w)=1π∫−∞∞f(u)cos⁡(wu)duA(w)=\frac{1}{π} ∫_{-∞}^{∞}f(u) cos⁡(wu)du 、 B(w)=1π∫−∞∞f(u)sin⁡(wu)duB(w)=\frac{1}{π} ∫_{-∞}^{∞}f(u)sin⁡(wu)du

(3). 若 f(x) 是偶函数，则 B(w)=0；若 f(x) 是奇函数，则 A(w)=0。

(ex.53) 若 当当f(t)={1,当|x|<10,当|x|>1f(t)=\begin{cases} 1,当|x|<1\\[2ex] 0,当|x|>1\\[2ex] \end{cases} ，求其傅立叶级数。

Sol： A(w)=1π∫−∞∞f(u)cos⁡(wu)du=1π∫−11cos⁡(wu)du=sin⁡(wu)π∙w|1−1=2sin⁡(w)π∙wA(w)=\frac{1}{π} ∫_{-∞}^{∞}f(u) cos⁡(wu)du=\frac{1}{π} ∫_{-1}^{1}cos⁡(wu)du=\frac{sin⁡(wu)}{π∙w}|\begin{matrix} 1\\-1\\ \end{matrix}=\frac{2sin⁡(w)}{π∙w}

B(w)=\frac{1}{π} ∫_{-∞}^{∞}f(u)sin⁡(wu)du=\frac{1}{π} ∫_{-1}^{1}sin⁡(wu)du=\frac{cos⁡(wu)}{π∙w}|\begin{matrix} 1\\-1\\ \end{matrix}=0

所以 f(x) 的傅立叶积分 =\frac{2}{π}∫_{0}^{∞} \frac{cos⁡(wx)sinw}{w} dw

傅立叶余弦与正弦变换

(1). fc(w) 称为 f(x) 的“傅立叶余弦变换” (其中，c 表示 cos)， f_c(w)＝-\sqrt{\frac{2}{π}} ∫_{0}^{∞}f(x)cos(wx)dx

(2). f(x) 称为 f(x) 的“反傅立叶余弦变换”， f_c(x)＝\sqrt{\frac{2}{π}} ∫_{0}^{∞}f_c(w)cos(wx)dx

(3). fs(w) 称为 f(x) 的“傅立叶正弦变换” (其中，s 表示 sin)， f_c(w)＝\sqrt{\frac{2}{π}} ∫_{0}^{∞}f(x)sin(wx)dx

(4). f(x) 称为 f(x) 的“反傅立叶正弦变换” (其中，c 表示 cos)， f_c(x)＝-\sqrt{\frac{2}{π}} ∫_{0}^{∞}f_s(w)sin(wx)dx

(5). 它们在某些应用中仍然是首选，例如信号处理或统计。

(ex.54) 若 f(t)=\begin{cases} 1,当0<x<a\\[2ex] 0,当x>a\\[2ex] \end{cases} ，求其 (1).傅立叶余弦级数；(2).傅立叶正弦级数。

Sol：

(1). 傅立叶余弦转换， f_c(w)＝\sqrt{\frac{2}{π}} ∫_{0}^{∞}f(x)cos(wx)dx=\sqrt{\frac{2}{π}} ∫_{0}^{∞}1∙cos(wx)dx=\sqrt{\frac{2}{π}}∙[\frac{sin(aw)}{w}]

(2). 傅立叶正弦转换，

f_s(w)＝\sqrt{\frac{2}{π}} ∫_{0}^{∞}f(x)sin(wx)dx=\sqrt{\frac{2}{π}} ∫_{0}^{∞}1∙sin(wx)dx=\sqrt{\frac{2}{π}}∙[\frac{1-cos(aw)}{w}]

离散傅立叶变换

(1). 在数字影像处理或通信系统的应用中，所处理的数据都是离散 (非连续) 数值。

(2). 令 f(x) 是周期为 2π 的周期函数 (0≦x≦2π)，对 f(x) 做 N 次相同“间隔点”(是离散数值)的量测，即间隔点为 x_k=\frac{2πk}{N}，k=1, 2, …., N-1，量测到的值是 \vec{f}\ =[f_o, f_1, f_2, …f_{N-2}, f_{N-1}]^T

注： \vec{f}\ 符号上面有箭头，表示其为向量。

(3). 则 f(x) 的离散傅立叶变换 \vec{f^A_{n}}\ =\vec{F_N}\ ・\vec{f}\ ，即

\begin{bmatrix} f_0^{A} \\ f_1^{A} \\ .\\ .\\ .\\ f_{N-1}^{A} \end{bmatrix} = \begin{bmatrix} w^{0-0} & w^{0-1} & ... & w^{0∙(N-1)}\\ w^{1-0} & w^{1-1} & ... & w^{1∙(N-1)} \\ .\\ .\\ .\\ w^{(N-1)∙0} & w^{(N-1)-1} & ... & w^{(N-1)∙(N-1)} \end{bmatrix} \begin{bmatrix} f_0 \\ f_1 \\ .\\ .\\ .\\ f_{N-1} \end{bmatrix}

其中，

(a). F_N 為 NxN 傅立叶矩阵。

(b). w^{a∙b} 的 a・b 是矩阵行与列位置的相乘，因 F_N 為 NxN 矩阵，有时候 w^{a∙b} 會寫成 w_N^{a∙b}

(c). w=e^{\frac{-2πi}{N}} 。

(d). w^n=e^{\frac{-2πni}{N}}=cos⁡(\frac{-2πn}{N})+isin(\frac{-2πn}{N})

(ex.55) 令 N=4 次量测 (取样值)，量到的值为 f=[4, 1, 1, 4]^T ，此离散傅立叶变换为何？

Sol： \begin{bmatrix} f_0 \\ f_1 \\ f_2 \\ f_3 \end{bmatrix} ＝ \begin{bmatrix} w^0 & w^0 & w^0 & w^0\\ w^0 & w^1 & w^2 & w^3 \\ w^0 & w^2 & w^4 & w^6\\ w^0 & w^3 & w^6 & w^9 \end{bmatrix} \begin{bmatrix} f_0 \\ f_1 \\ f_2 \\ f_3 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & -i & -1 & i \\ 1 & -1 & 1 & -1\\ 1 & i & -1 & -i \end{bmatrix} \begin{bmatrix} 4 \\ 1 \\ 1 \\ 4 \end{bmatrix} = \begin{bmatrix} 10 \\ 3+3i \\ 0\\ 3-3i \end{bmatrix}

快速傅立叶变换

(1). 离散傅立叶变换的矩阵 NxN，若取样点有 1,000 点，其计算时间会很常，此时可以用快速傅立叶变换 (Fast Fourier Transform, FTF) 来解题。

(2). 快速傅立叶变换是将 N 分成 2 组，即 N=2M 来解。

(3). 将原向量 \vec{f}\ =[f_0, f_1 … f_{N-1}]^T 分解成二个包含 M 个分量的向量，及包含所有的偶数分量 \vec{f_{even}}=[f_0, f_2 … f_{N-2}]^T=[f_{even, 0}, f_{even, 2}, … ,f_{even, M-1}]^T ，和包含所有的奇数分量 f_{odd}=[f_1, f_3, … f_{N-1}]^T=[f_{odd, 0}, f_{odd, 2}, … ,f_{odd, M-1}]^T

(注：有顶线的 f 表一向量，而无顶线的 f 表一纯量。)

(4). 分别对 f_{even} 和 f_{odd} 计算其离散傅立叶变换，可利用下列公式求得：

\vec{f_{even}^A}=[f^A_{{even}, 0}, f^A_{{even}, 1}, … ,f^A_{{even}, M-1}]^T＝\vec{F_Mf_{even}} ---(A)

\vec{f_{odd}^A}=[f^A_{{odd}, 0}, f^A_{{odd}, 1}, … ,f^A_{{odd}, M-1}]^T＝\vec{F_Mf_{odd}} ---(B)

(注：上面两个 F_M 是相同的。)

(5). 由 (A)、(B) 我们可以得到某一组量测点 f 的离散傅立叶变换，即为：

\begin{cases} f^A_n=f^A_{odd}+w^n_Nf^A_{odd},n＝0,1,…,M-1\\[2ex] f^A_{n+M}=f^A_{odd}-w^n_Nf^A_{odd},n＝0,1,…,M-1\\[2ex] \end{cases}

(ex.56) 令 N=4 次量测 (取样值)，量到的值为 f=[0, 1, 4 ,9]^T ，此离散傅立叶变换为何？

Sol：因 N=4，所以 M=\frac{N}{2}=2 ，而 W^0_M=(e^{\frac{-2πi}{2}})^0＝1 ，(M=2)， W^1_M=(e^{\frac{-2πi}{2}})^1＝cos(-π)+isin(-π)=-1

F_2=\begin{bmatrix} w^0 & w^0 \\ w^0 & w^1 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}

W^0_N=(e^{\frac{-2πi}{2}})^0=1 ，(N=4)，

W^1_N=(e^{\frac{-2πi}{2}})^1=cos(-\frac{π}{2})+isin(-\frac{π}{2})

由 (A) 式得 \vec{f_{even}^A}=\begin{bmatrix} f^A_0 \\ f^A_2 \end{bmatrix}=F_2\vec{f_{even}}=\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} f_0 \\ f_2 \end{bmatrix}=\begin{bmatrix} f_0+f_2 \\ f_0-f_2 \end{bmatrix}

由 (B) 式得 \vec{f_{odd}^A}=\begin{bmatrix} f^A_1 \\ f^A_3 \end{bmatrix}=F_2\vec{f_{odd}}=\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} f_1 \\ f_3 \end{bmatrix}=\begin{bmatrix} f_1+f_3 \\ f_1-f_3 \end{bmatrix}

由 (C) 式得 f^A_n=f^A_{even, 0}+w^n_Nf^A_{odd, 0}＝(f_0+f_2)+(f_1+f_3)＝f_0+f_1+f_3+f_4=0+1+4+9=14

由 (D) 式得 f^A_1=f^A_{even, 1}+w^n_Nf^A_{odd, 1}＝(f_0-f_2)-i(f_1+f_3)=f_0-if_1+f_2+if_3=0-i-4+9i=-4+8i

Ref.: