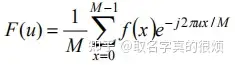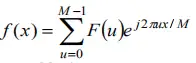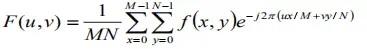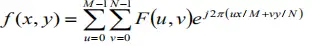1.对于图像傅里叶变换的理解
在了解一维的傅里叶变换之下,可以看出,二维离散傅里叶变换的基本思想是,将图像看成二维函数f,这个函数可以表示成两个维度上正弦和余弦函数的加权和。
首先给出一维离散傅立叶变换的公式,再给出了二维离散傅立叶的变换公式。直观地从两种离散傅里叶变换公式来看存在两处不同,但是对比两组不同却可以发现这两处不同都蕴含了加权的思想。以下是我认为讲的很通俗易懂的文章。
https://zhuanlan.zhihu.com/p/99605178
一维离散傅里叶变换
一维离散傅里叶逆变换
二维离散傅里叶变换
二维离散傅里叶逆变换
还是把可能用到的库直接放在前面,方便调用。
from PIL import Image
from skimage.io import imread, imsave, imshow, show
import scipy.fftpack as fp
from scipy import ndimage, misc, signal
from skimage import data, img_as_float
from skimage.color import rgb2gray
from skimage.transform import rescale
import matplotlib.pylab as pylab
import numpy as np
import numpy.fft
import timeit
import PIL.ImageStat as stat
2.使用傅里叶变换进行时频转换,并且完成图像重建
考虑将信噪比作为一个参考指标,这里给出求信噪比的代码。
def signaltonoise(a, axis=0, ddof=0):
a = np.asanyarray(a)
m = a.mean(axis)
sd = a.std(axis=axis, ddof=ddof)
return np.where(sd == 0, 0, m/sd)
im = np.array(Image.open(./images/img.jpg))
print("information img :",np.size(im[:,1,1]),np.size(im[1,:,1]))
对图像进行傅立叶变换,再通过变换结果重建图像的代码如下。不管是从信噪比,还是从图像结果来看,原图和重建图都基本没有差别。因此在实际运用过程中,二维离散傅立叶变换在时频转换的同时,也能保证图像处理的精准度。
snr for the original image = 1.7085726432772814
snr for the image obtained after reconstruction = 1.7085726432772814
im = np.array(Image.open(./images/img.jpg))
print("information img :",np.size(im[:,1,1]),np.size(im[1,:,1]))
snr = signaltonoise(im, axis = None)
print("snr for the original image = ", str(snr))
freq = fp.fft2(im)
im1 = fp.ifft2(freq).real
snr = signaltonoise(im1, axis = None)
print("snr for the image obtained after reconstruction = ", str(snr))
assert(np.allclose(im,im1))
pylab.figure(figsize = (20, 10))
pylab.subplot(121), pylab.imshow(im, cmap = gray), pylab.axis(off)
pylab.title(original Image, size = 20)
pylab.subplot(122), pylab.imshow(im, cmap = gray), pylab.axis(off)
pylab.title(Image obtained after reconstruction, size = 20)
pylab.show()
3.绘制频谱图
显示傅立叶变换的幅度称为变换的频谱。由于傅立叶系数是复数,我们通过对复数求摸,即可得到傅立叶变换的频谱图。
im = np.array(Image.open(./images/img.jpg))
print("information img :",np.size(im[:,1,1]),np.size(im[1,:,1]))
freq = abs(fp.fft2(im))
freq2 = fp.fftshift(freq)
pylab.figure(figsize = (10, 10))
freq2 = (20*np.log10(0.1 + freq2)).astype(int)
pylab.imshow(freq2)
4.使用numpy.fft模块计算DFT的幅值和相位
为了方便观察,我们将原来的图像转换为灰度图像。可以从下面的图像中看出幅值一般随空间频率的增加而减小,其规律很容易被掌握,而相位的图像看起来杂乱无章。
im1 = rgb2gray(imread(./images/cat.jpg))
pylab.figure(figsize = (12, 10))
freq1 = fp.fft2(im1)
im1_ = fp.ifft2(freq1).real
pylab.subplot(2, 2, 1), pylab.imshow(im1, cmap = gray)
pylab.title(Original Image, size = 20)
pylab.subplot(2, 2, 2), pylab.imshow(20*np.log10(0.01 + np.abs(fp.fftshift(freq1))), cmap = gray)
pylab.title(FFT Spectrum Magnitude, size = 20)
pylab.subplot(2, 2, 3), pylab.imshow(np.angle(fp.fftshift(freq1)), cmap = gray)
pylab.title(FFT Phase, size = 20)
pylab.subplot(2, 2, 4), pylab.imshow(np.clip(im1_, 0, 255), cmap = gray)
pylab.title(Reconstructed Image, size = 20)
pylab.show()
5.直观了解相位的作用
为了直观了解相位和幅值的关系,假设利用一幅图像的频谱实分量和另一幅图像的频谱虚分量来看看重建的输出图像是否变得扭曲。
(代码还有问题,但是今天跨年写不下去了,明天改改再发,告辞!)
--------------分割线-------------
元旦节的当天,我更新了最后部分的代码!
首先导入了图像,通过离散傅里叶变换得到实部和虚部,再分别交叉重建得到结果图如下。根据运行结果可以看出,输出的图像的确变得扭曲。
测试图一
测试图二
运行结果图
im1 = np.array(Image.open(./images/img1.png).convert(L))
im2 = np.array(Image.open(./images/img2.png).convert(L))
freq1 = fp.fft2(im1)
freq2 = fp.fft2(im2)
pylab.figure(figsize = (20, 15))
im1_ = (fp.ifft2(np.vectorize(complex)(freq1.real, freq2.imag, )).real).astype(int)
im2_ = (fp.ifft2(np.vectorize(complex)(freq2.real, freq1.imag, )).real).astype(int)
pylab.subplot(211), pylab.imshow(np.clip(im1_, 0, 255))
pylab.title(Reconstruction Image (Re(F1) + Im(F2)),size = 20)
pylab.subplot(212), pylab.imshow(np.clip(im2_, 0, 255))
pylab.title(Reconstruction Image (Re(F2) + Im(F1)),size = 20)