一文读懂傅立叶变换处理图像的原理(傅立叶变换实现)
作者丨小白
来源丨小白学视觉

前言

数字图像现在已经成为我们日常生活的一部分。因此,数字图像处理变得越来越重要。如何提高图像的分辨率或降低图像的噪声一直是人们热门话题。傅立叶变换可以帮助我们解决这个问题。我们可以使用傅立叶变换将灰度像素模式的图像信息转换成频域并做进一步的处理。今天,我将讨论在数字图像处理中,如何使用快速傅立叶变换,以及在Python中如何实现它。操作流程如下 (从左到右):


与现实生活中的光波和声波不同,由于像素的不连续性,数字图像是离散的。这意味着我们应该实现离散傅立叶变换(DFT)而不是傅立叶变换。然而,离散傅立叶变换(DFT)常常太慢而不实用,这就是我选择快速傅立叶变换(FFT)进行数字图像处理的原因。
接下来让我们深入到每一部分,找出这些步骤背后的理论。
第一步:计算二维快速傅立叶变换
快速傅立叶变换(FFT)处理的结果是一个很难直接可视化的复数数组。因此,我们必须把它转换成二维空间。这里有两种方法可以可视化这个快速傅立叶变换(FFT)结果:1、频谱2、相位角

从图(d)(1)可以看出,四个角上有一些对称图案。这些图案可以在下一步中转换到图像的中心。
频谱图像中的白色区域显示出较高的频率。频谱图像中的角表示低频域。因此,结合以上两点,角上的白色区域表明:在低/零频域中存在高频率,这对于大多数图像来说是非常正常的情况。
另一方面,很难从图(d)(2)中识别出任何明显的图案,这并不代表快速傅立叶变换(FFT)的相位角完全没有用处,因为相位保留了图像所必需的形状特征。
第二步:将零频域部分移到频谱中心
二维快速傅立叶变换(FFT)具有平移和旋转特性,因此我们可以在不丢失任何信息的情况下移动频谱。我把零频域部分移到了频谱的中心,这使得频谱图像对人类更为可见。此外,这种转换可以帮助我们轻松实现高通/低通滤波器。
步骤3:与步骤2相反。将零频域部分移回原位置
步骤4:与步骤1相反。计算二维快速傅立叶逆变换。
步骤3和步骤4的过程是将频谱信息转换回灰度图像。它可以通过应用逆向移位和快速傅立叶变换(FFT)的逆运算来实现。
编码
在Python中,我们可以利用Numpy模块中的numpy.fft轻松实现快速傅立叶变换(FFT)运算操作。
在理解了傅立叶变换背后的基本理论之后,我们就可以研究如何控制频谱输出来处理图像了。首先,我们需要了解低/高通滤波器。
低通滤波器

低通滤波器是一种只允许低频谱通过的滤波器。图像中的低频谱意味着像素值变化缓慢。例如,图像中颜色变化较小的平滑区域(如新空白白纸的中心)被视为低频谱内容。
由于低通滤波器的输出只允许低频通过,对噪声等高频谱内容进行了阻塞,使得处理后的图像具有较少的噪声像素。因此,低通滤波器被广泛应用于图像的去噪。
高通滤波器

相反,高通滤波器是只允许高频谱通过的滤波器。图像中的高频谱意味着像素值变化很大。例如,图像中颜色变化较大的边缘区域,如两张重叠的白纸和黑纸之间的边缘,被认为是高频谱内容。
在图像中,通过做适当的重复计算来锐化原图像,能用适当的重复计算来锐化原始图像的图像,从高通滤波器的输出可获得图像中的边缘。这将增强原始图像的清晰度,使边缘更加清晰。
从图e(5)和图f(5),我们可以注意到这两个滤波器呈现不同的特性。低通滤波器倾向于保留图像中的整体信息。另一方面,高通滤波器试图辨别出图像中的变化。
在了解了前一节中的低通/高通滤波器的工作原理后,让我们继续认识滤波器形状。
理想的滤波器


在理想滤波器背后的概念非常简单:给定一个半径值D₀作为阈值,低通滤波器图(g)(1)在阈值下H(u,v)等于1,在阈值以上H(u,v)等于0。

相反,高通滤波器图(g)(2)在阈值下H(u,v)等于0,在阈值以上H(u,v)等于1。
巴特沃思(Btterworth)滤波器
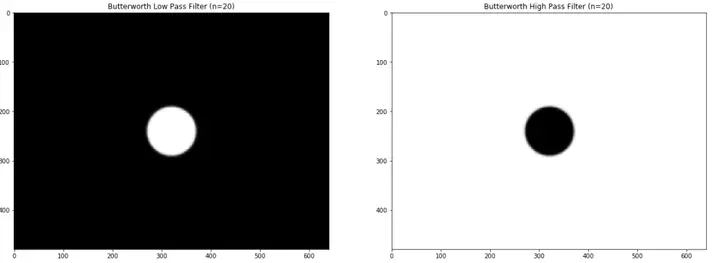
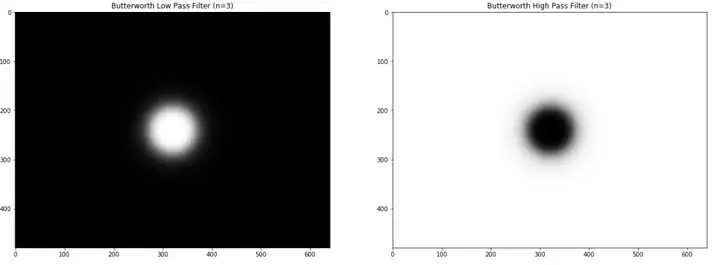
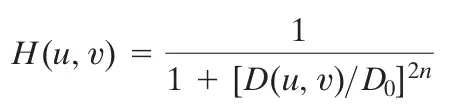
与理想滤波器不同的是,巴特沃斯滤波器没有明显的不连续性,使得通过的频率和被过滤的频率之间有明显的边界。巴特沃斯滤波器在函数中引入了一个新的参数n。当操作n时,它影响着通过的频率和被过滤的频率之间边界的清晰程度。具体可看图(h)和图(i)。
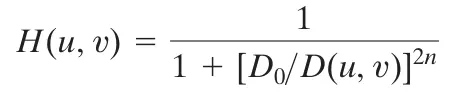
高斯(Gaussian)滤波器
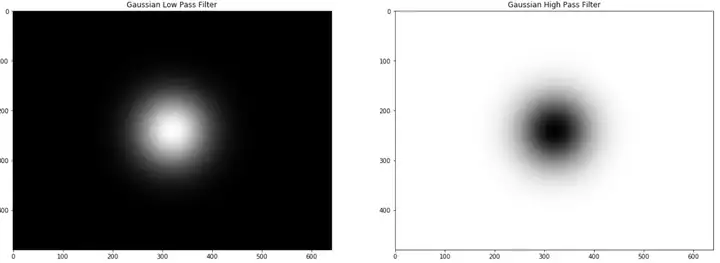
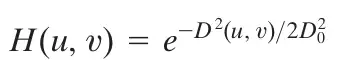
与巴特沃斯滤波器相比,高斯滤波器产生的边界更平滑。通过的频谱和被过滤的频谱之间的边界非常模糊,这便可以更平滑的处理图像。
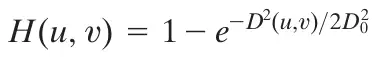
滤波器比较
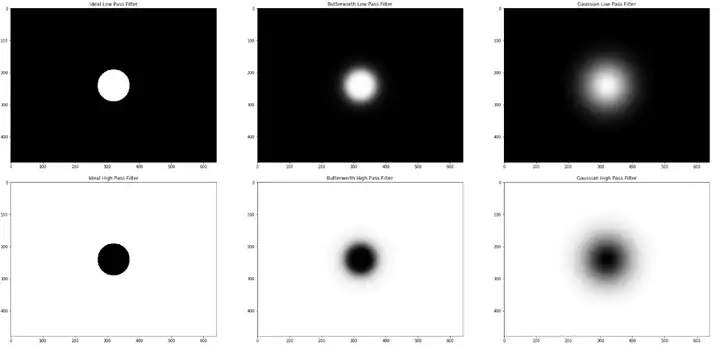
我把所有不同的过滤器放在图(k)中,以总结我们在过滤器设计中所做的工作。从左到右,圆的边缘变得模糊,这将对输出结果产生不同的影响总体上来看,巴特沃斯滤波器是介于理想滤波器和高斯滤波器之间的滤波器。
低通滤波器的结论

图(l)显示所有三个滤波器都是低通滤波器,因为输出图像保留了整个图像信息。此外,我们可以很容易地注意到高斯滤波器由于低失真比其他两个滤波器表现更好。理想滤波器产生大量波形噪声的原因是,理想滤波器的设计阻塞了距离原点一定半径以外的所有信息。因此,有些信息会在没有任何平滑的情况下急剧中断。相反,巴特沃斯滤波和高斯滤波是平滑的阻塞在距离原点一定半径之外的信息,这使得图像更平滑,失真更小。
高通滤波器的结论

毫无疑问,图(m)中的滤波器是高通滤波器,因为输出结果只捕获边缘。在滤波器中,高通滤波器结果的差异类似于低通滤波器结果。与巴特沃斯滤波器和高斯滤波器相比,理想滤波器的滤波结果有很多失真。
结束语
傅立叶变换是处理二维信息的有力工具。FT允许我们在另一个维度处理图像,这带来了更大的灵活性。在这篇文章中,我对使用傅立叶变换来处理图像这一基本步骤做了整理,希望小伙伴们喜欢。
往期精选
数据集汇总:
人脸识别常用数据集大全行人检测数据集汇总10个开源工业检测数据集汇总21个深度学习开源数据集分类汇总(持续更新)小目标检测、图像分类、图像识别等开源数据集汇总人体姿态估计相关开源数据集介绍及汇总小目标检测相关开源数据集介绍及汇总医学图像开源数据集汇总顶会资源:
CVPR 2022 全面盘点:最新250篇论文分方向汇总 / 代码 / 解读 / 直播 / 项目(更新中)CVPR22 最新106篇论文分方向整理|包含目标检测、动作识别、图像处理等32个方向一文看尽 CVPR2022 最新 22 篇论文(附打包下载)17 篇 CVPR 2022 论文速递|涵盖 3D 目标检测、医学影像、车道线检测等方向CVPR 2021 结果出炉!最新500篇CVPR21论文分方向汇总(更新中)CVPR 2021 结果出炉!最新600篇CVPR21论文分方向汇总(更新中)CVPR 2020 Oral 汇总:论文/代码/解读(更新中)CVPR 2019 最全整理:全部论文下载,Github源码汇总、直播视频、论文解读等CVPR 2018 论文解读集锦(9月27日更新)CVPR 2018 目标检测(object detection)算法总览ECCV 2018 目标检测(object detection)算法总览(部分含代码)CVPR 2017 论文解读集锦(12-13更新)2000 ~2020 年历届 CVPR 最佳论文汇总技术综述:
综述:图像处理中的注意力机制搞懂Transformer结构,看这篇PyTorch实现就够了熬了一晚上,我从零实现了Transformer模型,把代码讲给你听YOLO算法最全综述:从YOLOv1到YOLOv5图像匹配大领域综述!涵盖 8 个子领域,近 20年经典方法汇总一文读懂深度学习中的各种卷积万字综述|核心开发者全面解读Pytorch内部机制19个损失函数汇总,以Pytorch为例一文看尽深度学习中的15种损失函数14种异常检测方法总结PyTorch常用代码段合集神经网络压缩综述理论深挖:
深入探讨:为什么要做特征归一化/标准化?令人“细思极恐”的Faster-R-CNN论文盘点:
图像分割二十年,盘点影响力最大的10篇论文2020年54篇最新CV领域综述论文速递!涵盖14个方向:目标检测/图像分割/医学影像/人脸识别等实践/面经/求学:
如何配置一台深度学习工作站?国内外优秀的计算机视觉团队汇总50种Matplotlib科研论文绘图合集,含代码实现图像处理知多少?准大厂算法工程师30+场秋招后总结的面经问题详解深度学习三十问!一位算法工程师经历30+场CV面试后总结的常见问题合集(含答案)深度学习六十问!一位算法工程师经历30+场CV面试后总结的常见问题合集下篇(含答案)一位算法工程师从30+场秋招面试中总结出的目标检测算法面经(含答案)一位算法工程师从30+场秋招面试中总结出的语义分割超强面经(含答案)Github优质资源:
25个【Awsome】GitHub 资源汇总(更新中)超强合集:OCR 文本检测干货汇总(含论文、源码、demo 等资源)2019-2020年目标跟踪资源全汇总(论文、模型代码、优秀实验室)以上就是关于《一文读懂傅立叶变换处理图像的原理(傅立叶变换实现)》的全部内容,本文网址:https://www.7ca.cn/baike/66042.shtml,如对您有帮助可以分享给好友,谢谢。
