机器人基础知识:旋转矩阵-机器人学 旋转矩阵
机器人基础知识:旋转矩阵的总结
自己学习期间的复习总结,知识来源于上课教材“Skript zur Vorlesung Robotik1",由于水平有限,有错误还望各位及时指出。
本文提纲:
一、(右手系)笛卡尔坐标,向量的表达
二、旋转矩阵(含部分推导)
三、Kardan-角,Gimbal-lock问题,Euler-角,RPY-角
四、总结
关于旋转矩阵,我们首先要明确几个点:
被旋转的是什么? (向量)旋转后我们得到的“被旋转”体什么变了,什么没变?(向量本身没变,变得是向量在不同坐标系下的表达方式)如何进行旋转?有几种旋转的运算/表达方式。(使用旋转矩阵进行旋转结果的计算,有欧拉角,四元数等多种表达方式)
在回答上述问题前,我们要先看一下一些基本点,例如:坐标系统、向量等,在机器人学中我们一般使用3维几何空间的坐标系统,坐标系统一般我们会用(右手系)笛卡尔坐标,如图:
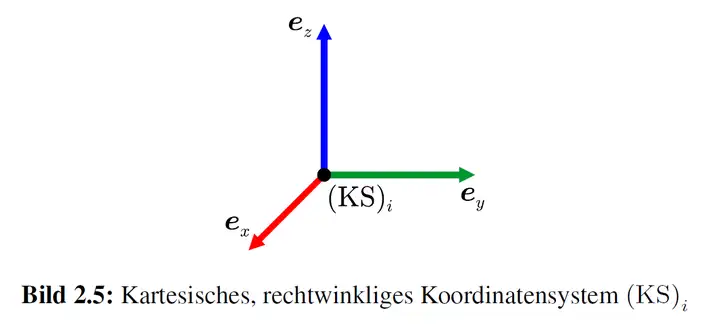
一、(右手系)笛卡尔坐标,向量的表达
右手系的笛卡尔坐标具有以下性质:
它的基向量:

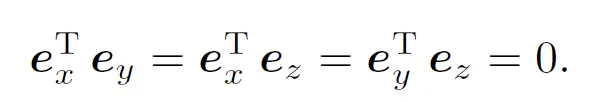

然后我们假设有2个坐标系,分别为坐标系(KS)0,(KS)B,KS表示Koordiantensystem,也就是坐标系统。则在(KS)0中的一个向量设为(此向量为从(KS)0原点到(KS)B原点的向量):
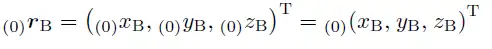
设一个点P到(KS)B原点的向量在(KS)B中表示为:
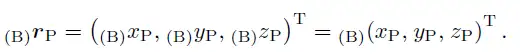
由于每个向量的坐标可以表示为向量在此坐标系中的xyz值和此坐标系的基底向量的点乘,故我们可以将这个向量写成这样的形式:
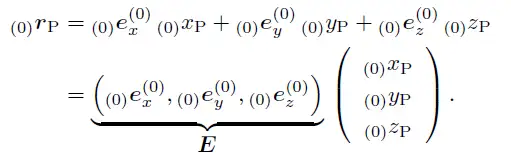
接下来我们要看一下向量的问题,首先向量是一种可以在空间中随意平移的一个量,因此在实际应用中我们要考虑一个机构的运动,不但需要向量表达方向和长度,还需要一个位置信息来确定机构之间的位置关系,但在此我们先不考虑这个位置的定位问题,只考虑旋转带来的变换,我们假设我们需要转的坐标系的原点没有发生平移,也就是仅围绕原点在旋转,那么我们可以将向量rBP写成:

此时R即为旋转矩阵。
二、旋转矩阵:
一个R旋转矩阵描述从(KS)B到(KS)0可以表示为:
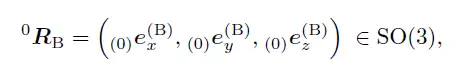
这些旋转矩阵具有以下性质:
由于通过旋转矩阵是正交的,故: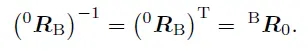
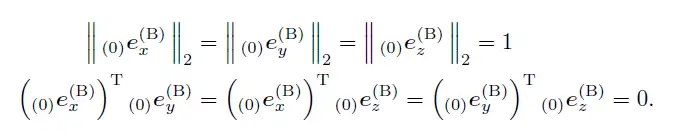

所谓单位旋转矩阵,就是指每次旋转只绕一个轴旋转一个角度(以下例子都是基于顺时针旋转):

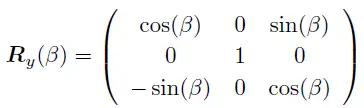
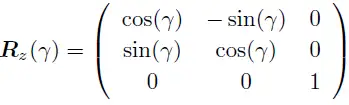
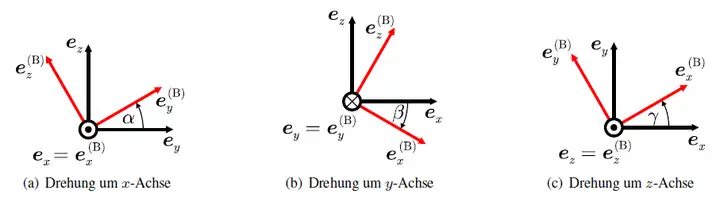
【此处的旋转矩阵表达的都是从红色到黑色坐标系】
组合旋转组合旋转就是不再是绕单一轴旋转了,是一个复合的旋转,但分解开来就是多个单位旋转的组成。(此时需要注意,R1R2不等于R2R1,也就是先旋转和后旋转的作用不同,如下图所示)
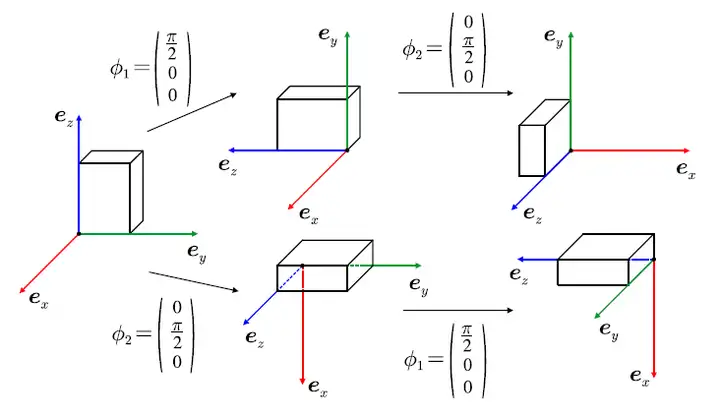
描述复合旋转有多种方式,例如Kardan-,Euler-,以及RPY-Winkel等。
这些旋转的表示方式也有一些不同,在此分为右乘类,和左乘类:
右乘类:
也就是计算旋转矩阵时,从左向右做矩阵乘法,描述的旋转是基于上一次旋转后(也就是当下)坐标的再次旋转。
左乘类:
也就是计算旋转矩阵时,从右向左做矩阵乘法,描述的旋转是基于最初那个“固定”坐标系的。
三、下面我们分开说明一下多种复合旋转矩阵:
Kardan-Winkel(Kardan角):
它的表达方式是基于右乘的,也就是每次单位旋转基于当前坐标,表达如下:
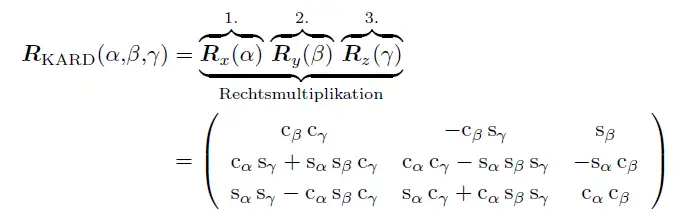
123表示旋转顺序,先1后2再3。
Gimbal-lock 问题:(对于右乘的旋转)
Gimbal-lock问题是指一种现象,这种现象是:当两个旋转轴重合时(此时产生的结果角度相当于旋转两次的结果,而实际上进行了三次旋转,也就是损失了一个自由度),在反向问题时(在机器人运动学中,从q:运动角度到x:点的位置是正向问题,反之从x到q是反向问题;在此处为从角度得到旋转矩阵为正,从旋转矩阵得到角度为反)会得到一个无穷解,因为此时相当于有一个方程,但有两个未知数。也就是这个结果可以只通过两个旋转轴的旋转就可以得到,但现在用了3次旋转,也就是损失了一个自由度(此时也是Singulare 情况,在矩阵上表达就是矩阵丧失了一个列或行)
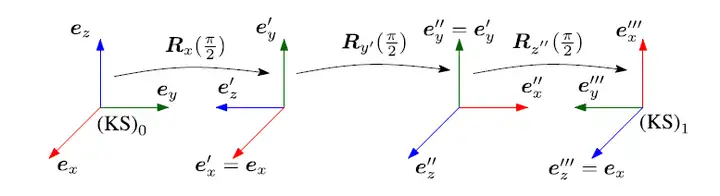
Euler-Winkel欧拉角(右乘):
Euler与Kardan没有实质区别,主要是旋转表达的区别:Kardan是分别绕三个不同的轴旋转3次,而Euler是第一次和第三次绕的轴为同一个轴,例如第一次为x轴,第三次也是x轴。欧拉角存在很多不同的定义,区别主要在旋转轴的选择,一共有12种情况,例如x轴:
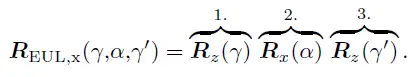
y轴:
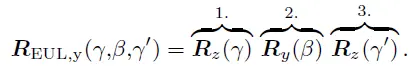
z轴:
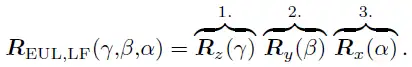
RPY-Winkel(BPY-角,左乘):
旋转的表达是绕着最初那个“固定”的坐标系进行的,在此使用左乘。
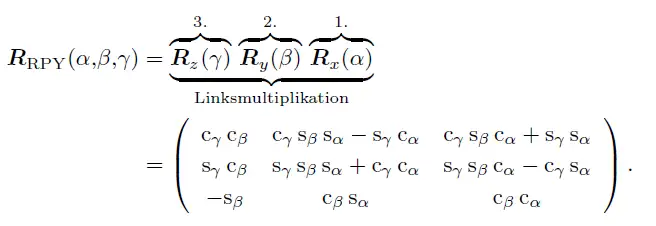
正向计算旋转矩阵:
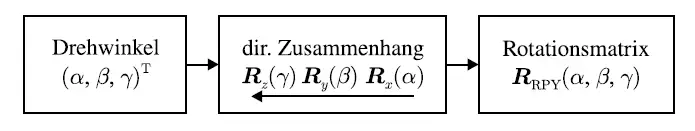
反向计算旋转角

四、总结:
采用旋转矩阵进行方向转换的计算有以下优缺点:
优点:
表达方式简单表达方式便于直观理解参数不多缺点:
在同一个表达方式的名称下有太多种不同的可能,例如Euler表达下有12种可能性相乘的顺序会影响结果Gimbal-Lock问题会出现在“伴随旋转”(也就是右乘)坐标系统转换中对角度的插值计算会有不可预见的路径出现以上就是关于《机器人基础知识:旋转矩阵-机器人学 旋转矩阵》的全部内容,本文网址:https://www.7ca.cn/baike/71968.shtml,如对您有帮助可以分享给好友,谢谢。
