矩阵4个子空间的物理意义：基尔霍夫定律与欧姆定律_矩阵空间的一组基

 

1.矩阵的四个子空间

前几篇文章讨论了矩阵的左、右、内、外四种乘法，并非要说明茴香豆的四种写法，而在于讨论矩阵四子：行、列、零、左四个子空间本文进一步做个拓展，通过电路来探讨一下矩阵四子的物理意义理解了该矩阵的四个子空间，也就抓住了线性代数的中心思想。

2.矩阵四个基本子空间

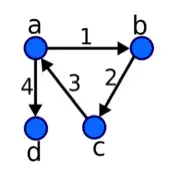
关系矩阵(Incidence Matrix)是一种表示对象关系的方法：每行表示一条边，每列表示一个节点，1和-1表示流出和流入[1]。

3.矩阵的子空间是什么意思

4个节点，4条边的图上图的关系矩阵(Incidence Matrix)为：A=[1−10001−10−1010100−1]A=\begin{bmatrix} 1 &-1&0&0\\ 0 &1&-1&0\\ -1 &0&1&0\\ 1 &0&0&-1\\ \end{bmatrix}

4.矩阵生成的子空间的基和维数

，4行分别表示：边1从A流向B，边2从B流向C，边3从C流向A，边4从A流向D；第1列表示a节点的流入流出情况，依此类推AA 对应的方程组是：{x1−x2=b1x2−x3=b2−x1+x3=b3x

5.矩阵的四个空间

1−x4=b4\begin{cases} x_1-x_2=b_1\\ x_2-x_3=b_2\\ -x_1+x_3=b_3\\ x_1-x_4=b_4 \end{cases} 对 AA 进行高斯消元（未交换行的顺序），得到：

6.矩阵的核空间的基

A′=[1−10001−10000000−11]A=\begin{bmatrix} 1 &-1&0&0\\ 0 &1&-1&0\\ 0 &0&0&0\\ 0&0&-1&1\\ \end{bmatrix}

7.方阵的子空间

第3行全为零，说明存在线性依赖，对应于电路中存在环电路中矩阵运算的物理意义：对于Ax=bA x= b ，输入xx 表示每个节点的电势(Potential)，输出 bb ,如b1=x1−x2b_1 = x_1-x_2。

8.矩阵空间的基和维数

等，表示节点AB间边1上的电势差(Potential Difference) / 电压；y=Cb y=C b 表示欧姆定律(Ohms Law)， yy 是每条边上的电流 ；ATy=0A^{T}y=0对应左零空间，

9.矩阵的四个子空间计算例题

即环路基尔霍夫电流定律；(ATy=ATCb=CATAxA^{T}y=A^{T}Cb=CA^{T}Ax)

10.矩阵的四大子空间关系

Gustav Robert Kirchhoff (12 March 1824 – 17 October 1887) 矩阵4子与电路零空间：零空间包含了 Ax=0Ax=0 的所有解，即 b=0b=0 ，于是：

x1=x2;x2=x3;x1=x4x_1=x_2;x_2=x_3;x_1=x_4 ，也就是说 x1,x2,x3,x4x_1,x_2,x_3,x_4 都相等，即特解x=[1111]x= \begin{bmatrix}1\\1\\1\\1\end{bmatrix}

是零空间 N(A)N(A) 的一个基， N(A)=[CCCC]N(A)=\begin{bmatrix}C\\C\\C\\C\end{bmatrix} 包含了使 Ax=0Ax=0 的所有解物理意义： b

=0b=0 表示所有节点（相互连接），电势均相等，电势差均为02. 行空间：边1，2，3构成了一个环(Loop)，就不独立了，对应的 AA 第3行 [−1010]\begin{bmatrix} -1 &0&1&0\\ \end{bmatrix} 。

等于第1行 [1−100]\begin{bmatrix} 1 &-1&0&0\end{bmatrix} 加第2行 [01−10]\begin{bmatrix} 0 &1&-1&0 \end{bmatrix}

再乘以 (−1)(-1) ，即：第3行依赖于第1，2行图存在环等价于矩阵中行或列存在依赖行空间垂直于零空间，点积等于0，取任一行与 [CCCC]\begin{bmatrix}C\\C\\C\\C\end{bmatrix}。

点积均等于0，行空间没有发现明显的物理意义，如果一定要说，那就是每条边连接2个节点，意义不大(Trival)3. 列空间：对应基尔霍夫电压定律 (Kirchhoff’s Voltage Law，KVL)，列空间是 。

AA 所有列的线性组合的集合，即：对所有可能的输入 xx 输出的 AxAx ，基尔霍夫电压定律告诉我们一个环/回路的电压和必须等于0选择任何一个满足基尔霍夫电压定律的 bb ，都存在一个对应的 xx 使得

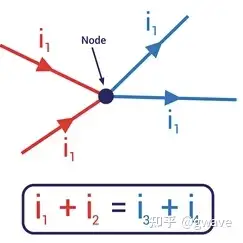
Ax=bAx=b 考虑：任意选择一个节点的电势，都能通过电势差计算出相邻节点的电势4. 左零空间：对应基尔霍夫电流定律 (Kirchhoff’s Current Law，KCL)，基尔霍夫电流定律告诉我们节点流入与流出电流的量相等。

ATy=[10−11−11000−110000−1][y1y2y3y4]=[0000]A^{T}y=\begin{bmatrix} 1 &0&-1&1\\ -1 &1&0&0\\ 0 &-1&1&0\\ 0 &0&0&-1\\ \end{bmatrix} \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4\\ \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ 0\\ 0\\ \end{bmatrix}

看下第1个方程： y1−y3+y4=0y_1- y_3+ y_4=0 ，节点 AA 流入与流出的电流和等于0(流入流出电流大小相等，符号相反)，第2、3、4方程分别对应B、C、D三个节点的电流和为0这个想法，不仅适用于电路，工程、科学、经济等领域都存在平衡的力或流。

这个不起眼的左邻空间蕴含着深意

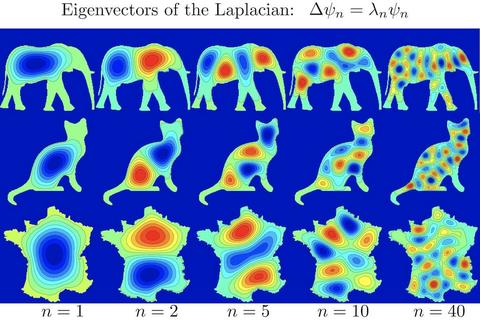
收费站应用基尔霍夫电流定律线性代数皇帝——对称矩阵 SS左零空间的ATy=ATCb=CATAx=0A^{T}y=A^{T}Cb=CA^{T}Ax=0 ，引出的对称矩阵 ATAA^{T}A 对应图拉普拉斯算符 (

graph Laplacian) LL ，也称基尔霍夫矩阵(Kirchhoff Matrix)，被用来在图中发现许多有用的属性，在谱聚类和图神经网络等算法中起关键作用；也可被用来构建机器学习热爱的低维度嵌入。

gwave：谱聚类(1)：图拉普拉斯算符122 赞同 · 6 评论文章

gwave：矩阵乘法核心思想（4）：左零空间120 赞同 · 13 评论文章

秩与欧拉示性公式零空间 N(A)=[CCCC]N(A)=\begin{bmatrix}C\\C\\C\\C\end{bmatrix} 是4维空间 R4R^{4} 中的一条线，它的维度是1，这意味 AA 的秩：

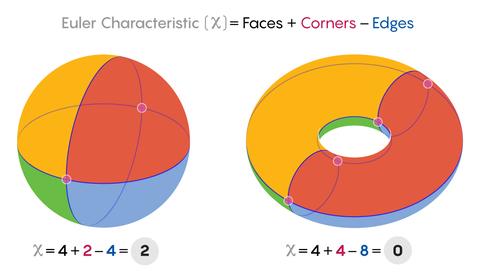
Rank(A)=r=4−1=3Rank(A)= r=4-1=3 ，也说明电路中存在1个环节点数：4边数：4环数：1面数：2节点数 - 边数 + 环数 = 4 - 4 + 2 = 2，即欧拉示性公式gwave：第2美数学公式、甜甜圈与宇宙的结构（1）：欧拉示性公式

18 赞同 · 3 评论文章

由此，我们能知道所有四子的维度：行空间维度=列空间维度= rr : Dim(C(AT))=Dim(C(A))Dim(C(A^{T})) =Dim(C(A)) =r=3=r=3 ； 零空间维度 :

Dim(N(A))Dim(N(A^{})) =n−r=1=n-r=1 ； 左零空间维度: Dim(N(AT))Dim(N(A^{T})) =m−r=1=m-r=1相关阅读gwave：线性代数“正交”全家桶(2) ：正交子空间

145 赞同 · 9 评论文章

参考^也有符号相反的用法