manim 中的矢量图（mane中文）

2023-07-24 19:47:29 阅读：

前言

原文地址

manim中的矢量图widcardw.github.io/2021/06/24/manim%E4%B8%AD%E7%9A%84%E7%9F%A2%E9%87%8F%E5%9B%BE/

博主本人只是对 manim 进行了一点点研究，并把成果分享给大家，文章中如有表述不当或错误，欢迎大家积极评论指出！谢谢！

widcardw 2021.06.27

在接触 manim 中的矢量图之前，大家最好先了解一下矢量图这一个概念，以便于更好地理解 manim 对于矢量图的处理方式。

同时，我也在很早以前将这个教程做成了视频，不过一直都没有写博客。视频传送门

[manim 教程] 自定义物件-矢量图_哔哩哔哩_bilibiliwww.bilibili.com/video/BV1364y1y71n

矢量图

网站推荐

MDN Web DocsW3school菜鸟

介绍

摘自百度百科

矢量图，也称为面向对象的图像或绘图图像，在数学上定义为一系列由点连接的线。矢量文件中的图形元素称为对象。每个对象都是一个自成一体的实体，它具有颜色、形状、轮廓、大小和屏幕位置等属性。

矢量图是根据几何特性来绘制图形，矢量可以是一个点或一条线，矢量图只能靠软件生成，文件占用内在空间较小，因为这种类型的图像文件包含独立的分离图像，可以自由无限制的重新组合。它的特点是放大后图像不会失真，和分辨率无关，适用于图形设计、文字设计和一些标志设计、版式设计等。

如果我们以文本格式打开一个矢量图（以 svg 为例），那么就会看到类似这样的内容。

摘自菜鸟教程，详见 https://www.runoob.com/svg/svg-path.html

可以看到，文件的内容大致都是坐标，颜色，路径，填充等内容。也正是因为这一个因素，在一些动画软件如 Flash, Animation 中能够对矢量图进行图形的补间操作。而补间的本质，就是插值(interpolate)。这一部分将会在之后的动画模块里面详细阐述。

贝塞尔曲线

网站推荐

微软 - 贝塞尔曲线的三种类型Animated Bézier Curves怎么理解贝塞尔曲线 - 知乎cubic-bezier翔哥 & 颓废 - 贝塞尔曲线参数方程推导

介绍

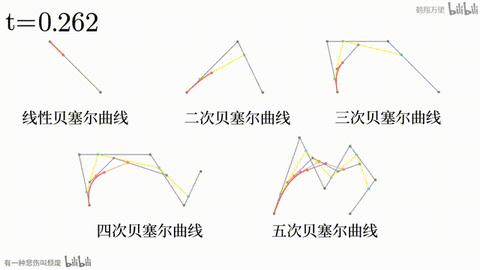
看过上面的几个网站之后，我相信读者对贝塞尔曲线应该有了一定的了解。用文字表述可能相当繁琐： $n$ n 条直线顺次相接，每条直线的一端有一个点，让这个点按一定规律从一头移动到另一头，再顺次连接这 $n$ n 个点，形成新的 $n-1$ n-1 条直线。对接下来的过程进行递归操作，直至只剩一个点时，这个点的运动轨迹。

但是用动画演示相对来说就更好理解了。

来自翔哥和颓废的视频

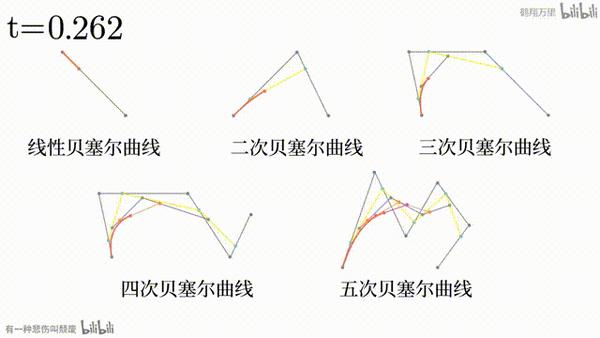
贝塞尔曲线的一般方程如下，其中 $Pi$ P_i 为创建贝塞尔曲线的 $n$ n 个点

$B(t)=\sumi=0n(ni)Pi(1-t)itn-i,t\in[0,1]$ B(t)=\sum_{i=0}^{n}\binom{n}{i}P_{i}(1-t)^{i}t^{n-i},t\in[0,1]

由于贝塞尔曲线可以算是纯靠坐标和计算机运算得到的一种图像，而且它也是构成矢量图的基本元素，因此在本篇中，它是最为核心的要素。

回到矢量图

基于贝塞尔曲线的知识，我们回到 svg 格式的路径，看到 <path> 标签的内容。

该部分内容来自 w3school

下面的命令可用于路径数据：

M = moveto

L = lineto

H = horizontal lineto

V = vertical lineto

C = curveto

S = smooth curveto

Q = quadratic Bezier curve

T = smooth quadratic Belzier curveto

A = elliptical Arc

Z = closepath

w3school 绘制曲线的例子

<?xml version="1.0" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg width="100%" height="100%" version="1.1" xmlns="http://www.w3.org/2000/svg"> <path d="M153 334 C153 334 151 334 151 334 C151 339 153 344 156 344 C164 344 171 339 171 334 C171 322 164 314 156 314 C142 314 131 322 131 334 C131 350 142 364 156 364 C175 364 191 350 191 334 C191 311 175 294 156 294 C131 294 111 311 111 334 C111 361 131 384 156 384 C186 384 211 361 211 334 C211 300 186 274 156 274" style="fill:white;stroke:red;stroke-width:2"/> </svg>

这里出现了我们的老朋友贝塞尔曲线。如果我们打开一个由 manim 生成的 Text 的 svg 文件，那么就会看到有大量的 C x1 y1 x2 y2 x3 y3，这就对应了二阶贝塞尔曲线中的三个二维坐标，回到上面的动图，看一眼它的生成过程，再体会一下用很多段二阶贝塞尔曲线拼接成一段完整的路径。

manim 中的矢量图

Vectorized Math Object

没错，就是这个非常神奇的类 VMobject，它就是所有平面几何图形和文字的父类。下面给出它的部分成员变量和方法。由于其中还涉及到关于上色、变换等元素，在这里只呈现部分与锚点相关的内容。

# 此处的 VMobject 为 manimgl 最新版 class VMobject(Mobject): CONFIG = { "fill_color": None, # 填充色 "fill_opacity": 0.0, # 填充色透明度 "stroke_color": None, # 轮廓颜色 "stroke_opacity": 1.0, # 轮廓透明度 "stroke_width": DEFAULT_STROKE_WIDTH, # 轮廓线宽 ..., "n_points_per_curve": 3, # 每条贝塞尔曲线由 3 个点构成 ... } ... def init_data(self): self.data = { "points": np.zeros((0, 3)), "bounding_box": np.zeros((3, 3)), "rgbas": np.zeros((1, 4)), } # 此处原本调用父类的方法，这里将方法补充完整 self.data.pop("rgbas") self.data.update({ "fill_rgba": np.zeros((1, 4)), "stroke_rgba": np.zeros((1, 4)), "stroke_width": np.zeros((1, 1)), "unit_normal": np.zeros((1, 3)) }) # 对于 VMobject 的上色方案进行了重写 ...

其中，n_points_per_curve 指示了一条贝塞尔曲线由 3 个锚点构成，而 VMobject 这个类允许用多条贝塞尔曲线来构成一系列的图形。我们可以使用 vmob.set_points([...]) 方法来设置它的形状。列表中放了所有构成这个图形的锚点，它的长度必须是 3 的倍数。下面给出一个例子，能够画出一个橄榄形。

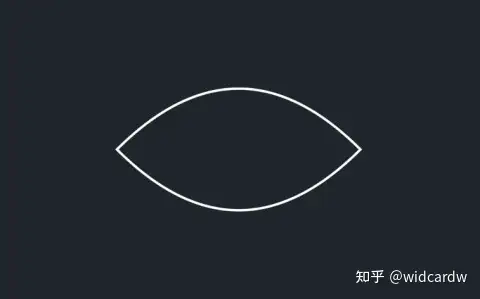
v = VMobject() v.set_points(np.array([ [-2, 0, 0], [0, 2, 0], [2, 0, 0], [2, 0, 0], [0, -2, 0], [-2, 0, 0] ]))

而其本质就是将两段贝塞尔拼接起来。下图即为加上锚点和手柄的图像。

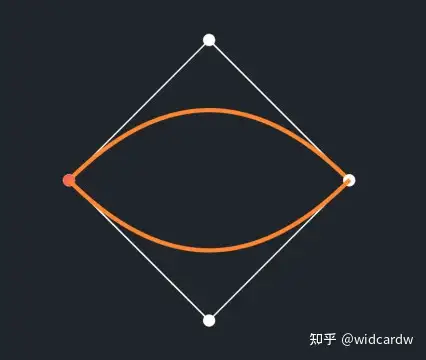
为何使用二阶贝塞尔

在旧版的 manim-cairo 中用的是三阶贝塞尔，新版 manimgl 中为二阶贝塞尔，本质区别不大。但肯定会有人好奇为什么可以用更高阶的贝塞尔曲线却不用。原因就在于贝塞尔曲线的参数方程 ~~再放送~~

$B(t)=\sumi=0n(ni)Pi(1-t)itn-i,t\in[0,1]$ B(t)=\sum_{i=0}^{n}\binom{n}{i}P_{i}(1-t)^{i}t^{n-i},t\in[0,1]

我们可以看到这其中包含了组合数，而组合数的运算包含了阶乘，这一运算符相对来说复杂度是比较高的。而虽然高阶贝塞尔曲线的方程可以通过使用递归，分解为一个个低阶数的来构成，但我们知道递归的复杂度在这种情况下会指数上升，在这里使用递归运算的速度可能还真的不如直接代数运算。

为了尽可能的降低运算的复杂度，人们就采用了低阶数的贝塞尔来拼接成一段完整的路径。从 w3school 的最后一个例子中，可以看到在 svg 的路径中也采用了多段二阶贝塞尔拼接成完整路径的方法。

从抽象到具象

从前面的基础知识到现在，终于可以讲一些具体的几何图形了。

如果大家翻过 geometry.py 文件的源码，可以发现不少几何图形都调用了父类 VMobject 的方法，例如 set_points_as_corners, add_line_to, close_path 等等，这些从方法名就基本上能看懂是什么意思，也可以阅读源码来理解它的运作方式。

曾有人说，直线就是不够弯的曲线。那么在 manim 中，直线就可以用 3 个在直线上均匀分布的锚点来构成。为什么说要均匀分布呢？虽然分布不均匀也可以构成直线，最多也不过加了一点拉扯，但为了运算方便，同时也为了减少 bug，在处理时就将这 3 个锚点等距的放在一条线上。

关于在三个点在同一直线上拉扯的问题

在测试中，也出现了这样的 bug，发生原因大致是 shaders 上色之前使用了 interpolate 对坐标、颜色等属性进行了补间，导致出现了一些偏差。

使用下面的代码，会发现直线的粗细会有一些问题，甚至出现断裂。

图中数字为锚点的位置和编号。

v = VMobject() v.set_points(np.array([[-1, 0, 0], [3, 0, 0], [1, 0, 0]]))

从直线到曲线

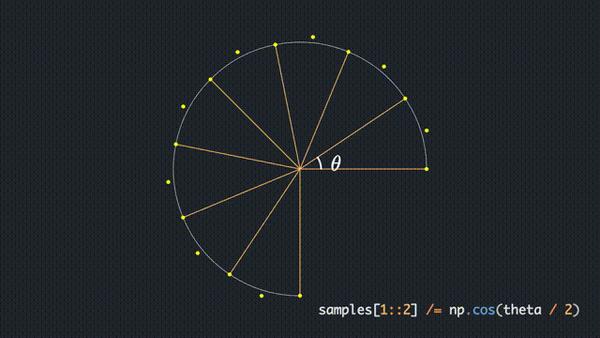
在刚刚贝塞尔曲线的介绍中，我们了解到了二阶贝塞尔拥有两个锚点，分别控制起点和终点，而还有一个手柄，可以控制曲线的弯曲程度。其中，圆弧就是通过这一方法来构成的，我们可以看一下圆弧类的一个静态方法，这个方法就是用来计算构成圆弧的一系列锚点的。在代码之后会放一段流程图说明其构造过程。

@staticmethod def create_quadratic_bezier_points(angle, start_angle=0, n_components=8): # n_components 表示一条圆弧用 8 条二阶贝塞尔曲线构成 # 从圆弧的开始到终止构造 17 个点 samples = np.array([ [np.cos(a), np.sin(a), 0] for a in np.linspace( start_angle, start_angle + angle, 2 * n_components + 1, ) ]) # 将圆弧的圆心角等分为 8 份，分别用贝塞尔曲线拟合 theta = angle / n_components # 将下标为奇数的点移动到偶数点处作切线相邻两者相交处 samples[1::2] /= np.cos(theta / 2) # 创建八条贝塞尔曲线的锚点 points = np.zeros((3 * n_components, 3)) points[0::3] = samples[0:-1:2] points[1::3] = samples[1::2] points[2::3] = samples[2::2] return points

函数图像曲线

在 manimlib/mobject/funcions.py 中，可以看到 ParametricCurve 这个类。它的意思本来是参数方程，但是它也可以用来画 $y=f(x)$ y=f(x) 的方程。FunctionGraph 就是继承它得到的。

从这个类的 init_points 方法中，我们可以大致的猜到，函数曲线是将定义域细分为很多个小段，在每一个小段上都对图像进行拟合，这里的拟合依然是用了一条二阶贝塞尔。在一定程度上分的越细，拟合的就越精确。

函数曲线的构建过程中还涉及到了使曲线变平滑的一些方法，博主目前还没有学到，因此在这里不过多的阐述。主要的一些方法有

change_anchor_modemake_smoothmake_approximately_smoothmake_jagged

文字

旧版的 manim 采用 cairo 库生成文字并将其转换为 svg 路径，而新版因为抛弃了 cairo 绘图，因此顺便也将 cairo 生成文字也抛弃了，使用了 Manim Community 开发的 ManimPango 库。

在矢量图的部分也提到了，路径大多是由很多段贝塞尔曲线拼接而成的，文字 svg 也不例外，而且恰好它们大多也都是二阶贝塞尔，与 manimgl 的矢量图相匹配。~~虽然现在文字的填充有时候还是会因为三角剖分的问题而变得鬼畜。~~那么，现在就可以把文字当作是一个几何图形来看待了，有轮廓，有填充色，能够进行变换。

矢量图的变换

从开头到现在，我们提到的能够直接构成矢量图形的只有贝塞尔曲线，而决定贝塞尔曲线的就是它的锚点。我们只需要对锚点进行坐标变换，就可以从最底层的方面来影响其表象了。

例如 scale 方法，无非就是将构成矢量图的所有点的坐标乘上一个数，如果有 about_point 参数，那就只是加一个相对坐标的运算罢了。

如果再复杂一些，例如在 $R3$ \mathbb{R}^3 空间的变换，只要你的数学足够好，那应当就不会有太大的问题，在 example_scenes.py 中 Grant 给出了一些例子，读者可以去研究一下。在 VMobject 中已经给出的一些变换方法如下

apply_functionapply_points_functionapply_complex_function···

矢量图的组合

VGroup

VGroup 类继承于 VMobject，不过它本身也可以作为一个容器，也就是说我们可以把它当作一个列表来看待，使用 add 和 remove 方法添加或删除元素，也可以通过方括号下标来进行索引。但是 VGroup 对于图层的适配是相当差的（其实 manim 本身就对图层适配很差）。

append_points

在 VMobject 中有一个方法 reverse_points，作用是将锚点反转。听上去这个反转好像并没有什么卵用，但实际上还是有不少使用例的，Annulus 环形实际上就是由两个相反的圆组合而成的。下面给出它的定义。

class Annulus(Circle): CONFIG = { "inner_radius": 1, "outer_radius": 2, "fill_opacity": 1, "stroke_width": 0, "color": WHITE, "mark_paths_closed": False, } def init_points(self): self.radius = self.outer_radius outer_circle = Circle(radius=self.outer_radius) inner_circle = Circle(radius=self.inner_radius) inner_circle.reverse_points() self.append_points(outer_circle.get_points()) self.append_points(inner_circle.get_points()) self.shift(self.arc_center)

可以看到，它的创建过程其实也相当简单，就是将内圆的点集反转，附加到外圆的点集中，再加上填充色，就变成圆环了。

为什么它会填充成一个圆环，而不是两次都向内填充呢？

可以这么思考：圆的一圈点集，是按照逆时针分布的，那么这条路径也可以看作是有向的，而上色机制会将向量的左边进行填充。将内圈的圆点集反转，那么路径方向也会反转，而上色机制同样对向量的左边进行填充。两者同时成立，得到的就是外圆扣去内圆的形状了。请忽略填充不完整的 bug

总结

本篇主要阐述了在 manim 中如何通过控制锚点来创建自定义物件（当然仅限于矢量图），用贝塞尔曲线来拟合图像的一些过程。总之就是通过修改底层（DNA）来控制表象（相对性状）~~什么玩意居然在这里扯生物~~。

如何显示锚点的位置和索引，可以自定义一个类，代码在这里给出。

class AllPointsIndex(VGroup): CONFIG = { "scale_factor": 0.5, "color": WHITE, } def __init__(self, obj, **kwargs): # digest_config(self, kwargs) VGroup.__init__(self, **kwargs) for index, points in enumerate(obj.get_all_points()): point_id = Integer(index, background_stroke_width=2) \ .scale(self.scale_factor).set_color(self.color) point_id.move_to(points) self.add(point_id)

以上就是关于《manim 中的矢量图（mane中文）》的全部内容，本文网址：https://www.7ca.cn/tg/40711.shtml，如对您有帮助可以分享给好友，谢谢。

标签:

声明