在数学的浩瀚星河中,二次函数犹如一颗兼具美感与实用价值的恒星,既以优雅的曲线形态展现着数学的对称之美,又在现实生活的诸多领域扮演着解决问题的关键角色。从抛出的篮球划过的轨迹,到喷泉喷洒的水流形成的弧线,再到桥梁设计中抛物线形的承重结构,二次函数的身影无处不在。它不仅是初中数学知识体系的重要组成部分,更是连接基础代数与高等数学的桥梁,为学习者打开通往更复杂数学领域的大门。理解二次函数的本质、性质及应用,不仅能够提升数学思维能力,更能让人在分析和解决实际问题时拥有更科学的视角与方法。
二次函数的定义看似简洁,却蕴含着严谨的数学逻辑。在代数范畴中,形如\( y = ax^2 + bx + c \)(其中\( a \)、\( b \)、\( c \)为常数,且\( a \neq 0 \))的函数被称为二次函数。这一表达式中的每一项都有着特殊的意义:\( a \)决定了函数图像的开口方向与宽窄程度,当\( a > 0 \)时,图像开口向上,函数存在最小值;当\( a < 0 \)时,图像开口向下,函数存在最大值;\( |a| \)的值越大,图像开口越窄,反之则越宽。\( b \)与\( a \)共同影响着函数图像的对称轴位置,对称轴公式为\( x = -\frac{b}{2a} \),而\( c \)则代表着函数图像与\( y \)轴交点的纵坐标,即当\( x = 0 \)时,\( y = c \)。这些参数的相互作用,共同塑造了二次函数图像 —— 抛物线的独特形态,也让二次函数拥有了丰富多变的性质。
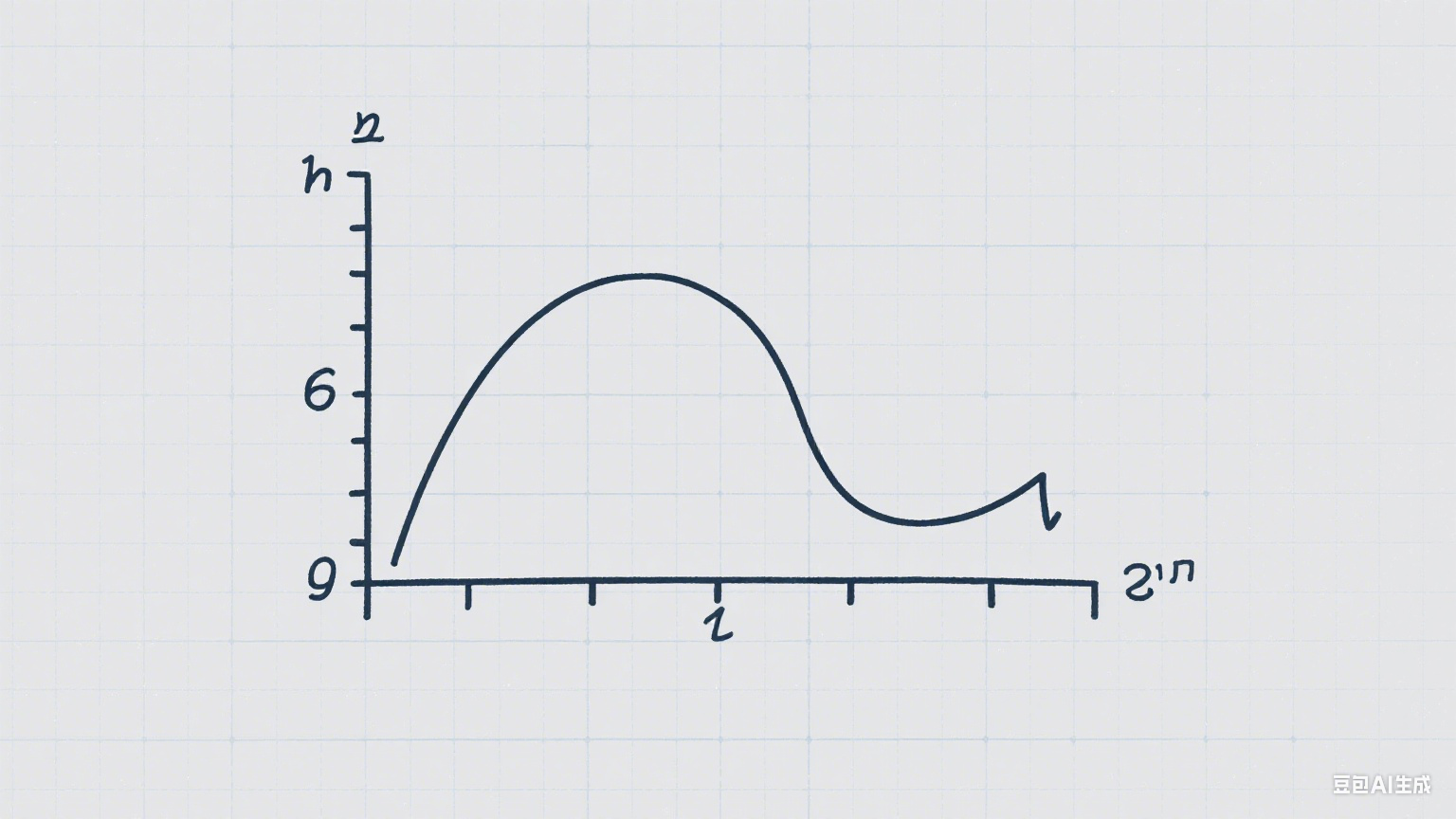
(注:此处为示例图片链接,实际使用时可替换为包含抛物线、对称轴、顶点、与坐标轴交点等关键元素的二次函数图像,直观展示不同参数对图像的影响)
深入探究二次函数的图像性质,能进一步发现其蕴含的数学规律。抛物线作为二次函数的几何表达,具有鲜明的对称性,对称轴便是其对称中心的 “脊梁”,图像上任意一点关于对称轴的对称点也必然在抛物线上。这种对称性不仅是视觉上的美感来源,更是解决数学问题的重要工具。例如,在求二次函数在某一区间内的最值时,若区间包含对称轴,那么函数在对称轴处取得最值;若区间不包含对称轴,则需根据函数的增减性判断最值位置。二次函数的增减性同样与开口方向和对称轴密切相关:当\( a > 0 \)时,抛物线开口向上,在对称轴左侧(\( x < -\frac{b}{2a} \)),函数值随\( x \)的增大而减小,在对称轴右侧(\( x > -\frac{b}{2a} \)),函数值随\( x \)的增大而增大;当\( a < 0 \)时,抛物线开口向下,增减性则与开口向上时完全相反。此外,二次函数的顶点是图像的 “最高点” 或 “最低点”,其坐标为\( (-\frac{b}{2a}, \frac{4ac – b^2}{4a}) \),顶点的纵坐标正是函数的最大值或最小值,这一性质在解决实际问题中的最值问题时有着广泛应用。
除了标准形式\( y = ax^2 + bx + c \),二次函数还有两种常见的表达形式,分别是顶点式和交点式,不同形式在解决不同类型问题时各有优势。顶点式为\( y = a(x – h)^2 + k \)(其中\( a \neq 0 \),\( (h, k) \)为抛物线的顶点坐标),这种形式能够直接体现二次函数的顶点位置,因此在已知顶点坐标或需要求函数最值时,使用顶点式会更加便捷。例如,若已知抛物线的顶点为\( (2, 3) \),且经过点\( (1, 5) \),只需将顶点坐标代入顶点式,再代入已知点求出\( a \)的值,即可快速得到函数表达式。交点式则为\( y = a(x – x_1)(x – x_2) \)(其中\( a \neq 0 \),\( x_1 \)、\( x_2 \)为抛物线与\( x \)轴交点的横坐标),当已知抛物线与\( x \)轴的两个交点时,交点式能让函数表达式的求解过程变得简单高效。比如,若抛物线与\( x \)轴交于\( (1, 0) \)和\( (3, 0) \),且经过点\( (2, -1) \),代入交点式后即可轻松求出\( a \)的值,进而得到完整的函数表达式。这三种形式之间可以通过代数变形相互转化,熟练掌握它们的转化方法,能极大提升解决二次函数相关问题的灵活性与效率。
二次函数的应用场景远超数学课本的范畴,在物理、经济、工程等多个领域都发挥着不可替代的作用。在物理学中,抛体运动是最典型的二次函数应用案例。当物体以一定的初速度斜向上抛出时,忽略空气阻力的情况下,物体在竖直方向上的位移与时间的关系遵循二次函数规律。设物体的初速度在竖直方向的分量为\( v_0 \),重力加速度为\( g \),则经过时间\( t \)后,物体在竖直方向的位移\( h \)可表示为\( h = v_0t – \frac{1}{2}gt^2 \),这正是一个开口向下的二次函数,其顶点对应的时间和位移分别为物体到达最高点的时间和最大高度,通过求解这个二次函数,就能准确预测抛体运动的轨迹和关键参数。在经济领域,二次函数常被用于成本、利润的分析与优化。例如,某企业生产某产品的成本包含固定成本和可变成本,可变成本与产量的平方成正比,而产品的售价与产量成线性关系,此时企业的利润就可以表示为关于产量的二次函数,通过求这个二次函数的最大值,就能确定最优的产量,实现利润的最大化。在工程设计中,抛物线形的结构因其良好的受力性能被广泛应用,如拱桥、隧道顶部、卫星天线等。以拱桥设计为例,为了让桥梁能够承受更大的荷载,工程师通常会将桥拱设计成抛物线形状,因为抛物线在承受均布荷载时,各点的应力分布均匀,能够有效分散压力,提升桥梁的稳定性和使用寿命,而这些设计的背后,都离不开二次函数的数学支撑。
在学习二次函数的过程中,许多学习者可能会遇到一些常见的难点,如对函数参数与图像关系的理解不透彻、在不同形式之间的转化出现错误、无法将实际问题抽象为二次函数模型等。针对这些难点,掌握科学的学习方法至关重要。首先,数形结合是学习二次函数的核心方法,通过绘制函数图像,将抽象的代数表达式与直观的几何图形结合起来,能够帮助学习者更清晰地理解参数\( a \)、\( b \)、\( c \)对图像的影响,以及函数的增减性、对称性、最值等性质。其次,多进行不同形式之间的转化练习,熟练掌握配方法(将标准形式转化为顶点式)、因式分解法(在合适的情况下将标准形式转化为交点式),并理解每种形式的适用场景,能够提升解决问题的灵活性。此外,在解决实际应用问题时,要学会从题目中提取关键信息,明确变量之间的关系,将实际问题抽象为数学模型,再利用二次函数的性质进行求解,最后还要对结果进行检验,判断其是否符合实际意义。通过不断的练习和总结,不仅能够攻克学习中的难点,还能培养用数学思维解决实际问题的能力。
二次函数作为数学领域的重要内容,其价值不仅体现在知识层面,更体现在对思维能力的培养和对现实世界的解释与改造上。它所蕴含的对称思想、数形结合思想、转化思想,不仅是解决数学问题的关键,更是分析和解决其他领域问题的重要思维工具。随着科技的发展和社会的进步,二次函数的应用场景还在不断拓展,从人工智能中的数据拟合,到航空航天中的轨迹计算,再到医学中的药物浓度变化分析,二次函数都在以不同的形式发挥着作用。对于学习者而言,深入理解二次函数,不仅是为了应对考试,更是为了掌握一种认识世界、解决问题的科学方法,那么在未来的学习和生活中,你还能发现哪些二次函数的应用案例?又将如何运用二次函数的知识去解决身边的实际问题呢?
免责声明:文章内容来自互联网,本站仅提供信息存储空间服务,真实性请自行鉴别,本站不承担任何责任,如有侵权等情况,请与本站联系删除。
