通信电子线路-振荡器_振荡器件

 

1.振荡器在通信系统的作用

反馈型自激振荡器 基本原理 运用调谐放大器电路，把经过放大的信号经过谐振回路选频得到输出信号，将输出信号通过反馈回送到输入端，假定回送的信号和输入信号的大小和相位相同，就可以形成自激振荡器

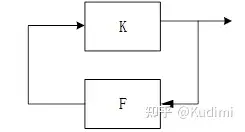
2.振荡器在通信中的作用

自激型振荡器框图K是电路放大倍数随着输入电压 ubeu_{be} 的改变有所改变 F是反馈系数，不随输入电压 ubeu_{be} 的改变而改变 产生自激振荡的条件： 反馈一定是正反馈 反馈到输入短的电压(电流)必须和输入电压(电流)同相

3.通用技术振荡电路

反馈信号足够大 起振条件和平衡条件假定放大倍数为 K ， 反馈系数为 F 起振振幅条件: 1">KF>1KF>1 振幅平衡条件: KF=1KF=1振幅稳定条件（能够自动回到平衡点）： dFdube|K

4.通信电路作用

=1F<0\[{\left. {\frac{{dF}}{{d{u_{be}}}}} \right|_{K = \frac{1}{F}}} < 0\]当 ubeu_{be} 增加的时候， K有所下降，这个时候

5.振荡器交流通路

KF<1KFKF>1KF>1 ， ubeu_{be} 会自动慢慢增大，恢复到A点

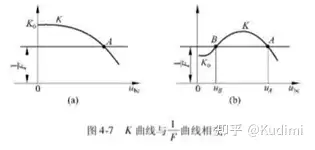
6.常用的振荡电路

振幅稳定条件示意图(b)中的B点是 0\]">dFdube|K=1F>0\[{\left. {\frac{{dF}}{{d{u_{be}}}}} \right|_{K = \frac{1}{F}}} > 0\]

7.通信电子电路

，当 ubeu_{be} 在B点附近变动的时候, ubeu_{be} 无法自行恢复到B点，不能平衡相位平衡条件: φK+φF=n×360∘\[{\varphi _K} + {\varphi _F} = n \times {360^ \circ }\]

8.振荡电路芯片

相位稳定(能够自动回到平衡点)条件: dφ0df|f=f0<0\[{\left. {\frac{{d{\varphi _0}}}{{df}}} \right|_{f = {f_0}}} < 0\]相位稳定和频率稳定实质上是一回事,因为振荡的角频率就是相位的变化率 ,所以当振荡器的相位发生变化的时候，频率也发生了变化。

9.通信电子线路等效电路图

当回路谐振的时候,LC回路相当于纯电阻，相位是0，当外界引入 +Δφ\[ + \Delta \varphi \] ，工作频率增加，LC回路失谐，回路呈现容性，产生 +Δφ0\[ + \Delta \varphi _0\]

10.通信电子电路原理

，抵消外界引入的相位偏差；当外界引入 的时候同理即：外界干扰引起的 的变化趋势和回路振荡频率变化方向相同 回路自身产生的 的变化趋势和回路振荡频率变化方向相反

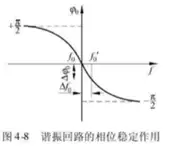
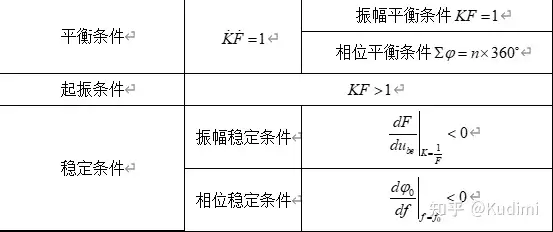
*振荡器的平衡、起振、稳定条件电容三点式振荡器（考毕兹电路）

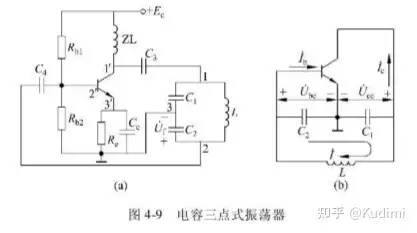
组成振荡器回路，作为晶体管放大器的负载阻抗 反馈信号从 取得，送回到放大器输入端 扼流圈ZL的作用是为了避免高频信号被旁路，为晶体管集电极构成直流通路，可以用大电阻R替代工作原理利用电容 将谐振回路的一部分电压反馈到基极上

将LC谐振回路的三个断电分别和晶体管三个电极相连 交流通路

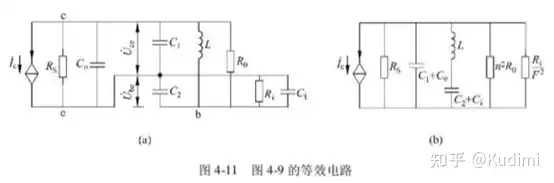
反馈系数(反馈信号和输出信号的比值) ： F=U˙ceU˙be≈C1+CoC2+Ci=C1′C2′\[F = \frac{{{{\dot U}_{ce}}}}{{{{\dot U}_{be}}}} \approx \frac{{C{}_1 + {C_o}}}{{C{}_2 + {C_i}}} = \frac{{{C_1}^\prime }}{{{C_2}^\prime }}\]

(C2′C_2 两端的压降和 C1′C_1 两端压降的比值) 放大倍数 ，输出信号和输入信号的比值：K=IcRΣIbRi=βIbRΣIbRi=βRΣRiRΣ=Rs//R0′//Ri′R0′=n2R0

=(C2′C1′+C2′)2R0Ri′=1F2Ri=(C2′C1′)2Ri\[\begin{array}{l} K = \frac{{{I_c}{R_\Sigma }}}{{{I_b}{R_i}}} = \frac{{\beta {I_b}{R_\Sigma }}}{{{I_b}{R_i}}} = \frac{{\beta {R_\Sigma }}}{{{R_i}}}\\ {R_\Sigma } = {R_s}//{R_0}^\prime //{R_i}^\prime \\ {R_0}^\prime = {n^2}{R_0} = {(\frac{{{C_2}^\prime }}{{{C_1}^\prime + {C_2}^\prime }})^2}{R_0}\\ {R_i}^\prime = \frac{1}{{{F^2}}}{R_i} = {(\frac{{{C_2}^\prime }}{{{C_1}^\prime }})^2}{R_i} \end{array}\]

其中：nn 是回路接入系数， FF 是反馈系数RcR_c 是LC回路谐振电阻， RiR_i 是晶体管输入电阻RsR_s 是晶体管输出电阻， CoC_o 是晶体管输出电容， CiC_i 是晶体管输入电容

（具体推导参考电容抽头接入，以及变换前后功率相等公式推导） 起振条件 1 \to \beta > \frac{{{R_i}}}{F}(\frac{1}{{{R_s}}} + \frac{1}{{{n^2}{R_0}}}) + F\xrightarrow{{{n^2}{R_0} > > {R_s}}}\beta > \frac{1}{F}\frac{{{R_i}}}{{{R_s}}} + F\]">

KF>1→β>RiF(1Rs+1n2R0)+F→n2R0>>Rsβ>1FRiRs+F\[KF > 1 \to \beta > \frac{{{R_i}}}{F}(\frac{1}{{{R_s}}} + \frac{1}{{{n^2}{R_0}}}) + F\xrightarrow{{{n^2}{R_0} > > {R_s}}}\beta > \frac{1}{F}\frac{{{R_i}}}{{{R_s}}} + F\]

振荡频率 为了保证相位平衡条件，振荡器的振荡频率基本和谐振频率相同f≈f0=12πLC=12πLC1′C2′C1′+C2′\[f \approx {f_0} = \frac{1}{{2\pi \sqrt {LC} }} = \frac{1}{{2\pi \sqrt {L\frac{{{C_1}^\prime {C_2}^\prime }}{{{C_1}^\prime + {C_2}^\prime }}} }}\]

实际振荡频率比上式中得出的稍微高一点 2.5 形成条件

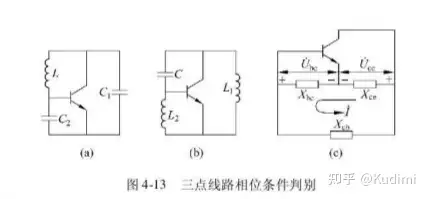
射同集反源同栅反晶体管的倒相作用使得 U˙ce\[{\dot U_{ce}}\] 和 U˙be\[{\dot U_{be}}\] 相位差为 为了保证正反馈，谐振回路的电抗性质必须让 U˙cb\[{\dot U_{cb}}\]

和 U˙be\[{\dot U_{be}}\] 的相位差也是 π\pi如图(c)中， U˙be\[{\dot U_{be}}\] 和 U˙ce\[{\dot U_{ce}}\] 的相位差是 π\pi

(本身带有),因此 XbeX_{be} 、 XceX_{ce} 之间不需要引入额外的相位差，电抗性质相同若要使 U˙cb\[{\dot U_{cb}}\] 和 U˙be\[{\dot U_{be}}\]

同向， XcbX_{cb} 的引入必须让 U˙cb\[{\dot U_{cb}}\] 和 U˙be\[{\dot U_{be}}\] 产生一个 π\pi 的相位差，因此 XcbX_{cb} 的电抗特性要和

XbeX_{be} 、 XceX_{ce} 相反当X为LC串联回路或是并联回路时，可以根据相频曲线判断

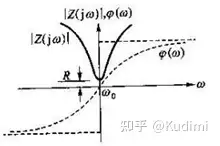
LC串联回路相频曲线

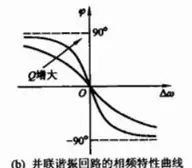
LC并联回路相频曲线克拉泼电路和西勒电路的优点缺点克拉泼电路(串联改进型电容三点式电路)

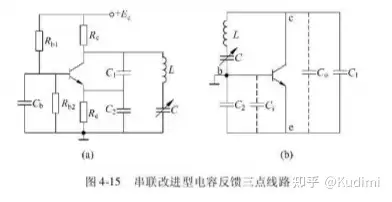
优点：可以提高频率稳定度，振荡频率为：ω0=1LCΣ1CΣ=1C+1C0+C1+1C2+Ci\[\begin{gathered} {\omega _0} = \frac{1}{{\sqrt {L{C_\Sigma }} }} \hfill \\ \frac{1}{{{C_\Sigma }}} = \frac{1}{C} + \frac{1}{{{C_0} + {C_1}}} + \frac{1}{{{C_2} + {C_i}}} \hfill \\ \end{gathered} \]

当 >C、C_2>>C">、C1>>C、C2>>CC_1>>C、C_2>>C 的时候：1CΣ≈1C\[\frac{1}{{{C_\Sigma }}} \approx \frac{1}{C}\]此时的振荡频率：

ω0≈1LC\[{\omega _0} \approx \frac{1}{{\sqrt {LC} }}\] 此时振荡频率和 C1C_1 、 C2C_2 没有什么关系了，提高了稳定度 缺点：如果 C1C_1

、 C2C_2 过大，振荡幅度就太低当减小C来提高振荡频率是，振荡幅度会显著下降，C减小到一定程度时候会停止振荡用作频率可调的振荡器时候，振荡幅度随着频率的增加而下降，在波段范围内不平等，因此频率覆盖系数(高端频率和低端频率之比称为频率覆盖系数)

西勒电路(并联改进型电容反馈三点式电路)

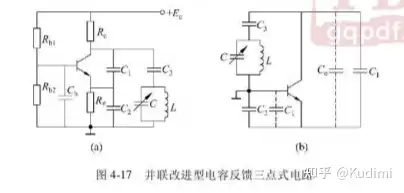
振荡频率：ω0=1LCΣCΣ=C+11C1+Co+1C2+Ci+1C3\[\begin{gathered} {\omega _0} = \frac{1}{{\sqrt {L{C_\Sigma }} }} \hfill \\ {C_\Sigma } = C + \frac{1}{{\frac{1}{{{C_1} + {C_o}}} + \frac{1}{{{C_2} + {C_i}}} + \frac{1}{{{C_3}}}}} \hfill \\ \end{gathered} \]

当 > {C_3}、{C_2} > > C{}_3\]">、C1>>C3、C2>>C3\[{C_1} > > {C_3}、{C_2} > > C{}_3\] ，则 CΣ≈C+C3\[{C_\Sigma } \approx C + {C_3}\]

消除了 CoC_o 、 CiC_i 对振荡频率的影响 优点 消除了 CoC_o 、 CiC_i 对振荡频率的影响 易于起振，在波段范围内幅度比较稳定 频率覆盖系数比较大 频率稳定性好，振荡频率可以提高

石英振荡器

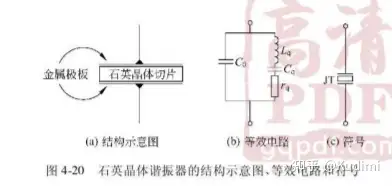
串联谐振频率 等效电路中 、Lq、CqL_q、C_q 组成串联谐振回路，串联谐振频率 f0f_0 为： f0=12πLqCq\[{f_0} = \frac{1}{{2\pi \sqrt {{L_q}{C_q}} }}\]

并联谐振频率 如果把 CoC_o 考虑进去那么 、、Lq、Cq、CoL_q、C_q、C_o 组成并联谐振回路，并联振荡频率为 fpf_p ： fp=12πC0CqC0+Cq\[{f_p} = \frac{1}{{2\pi \sqrt {\frac{{{C_0}{C_q}}}{{{C_0} + {C_q}}}} }}\]

由于一般来说， C_q">Co>CqC_o>C_q ，串联谐振频率和并联谐振频率相隔很近 两者关系可以如下：fp=12πC0CqC0+Cq=12πLqCqC0+CqC0=f01+CqC0\[{f_p} = \frac{1}{{2\pi \sqrt {\frac{{{C_0}{C_q}}}{{{C_0} + {C_q}}}} }} = \frac{1}{{2\pi \sqrt {{L_q}{C_q}} }}\sqrt {\frac{{{C_0} + {C_q}}}{{{C_0}}}} = {f_0}\sqrt {1 + \frac{{{C_q}}}{{{C_0}}}} \]

当有 >C_q">Co>>CqC_o>>C_q 的时候 CqC0<<1\[\frac{{{C_q}}}{{{C_0}}} < < 1\] ，利用等价无穷小 1+x≈1+x2\[\sqrt {1 + x} \approx 1 + \frac{x}{2}\]

展开： fp≈f0(1+Cq2C0)\[{f_p} \approx {f_0}(1 + \frac{{{C_q}}}{{2{C_0}}})\] 电抗特性

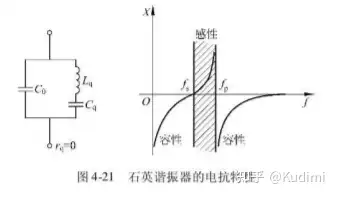
当不计算动态电阻 rqr_q 时的等效阻抗：Z=j(ωLq−1ωCq)(1jωC0)j(ωLq−1ωCq−1ωC0)=−j1ωC01−(ωsω)21−(ωpω)2\[Z = \frac{{j(\omega {L_q} - \frac{1}{{\omega {C_q}}})(\frac{1}{{j\omega {C_0}}})}}{{j(\omega {L_q} - \frac{1}{{\omega {C_q}}} - \frac{1}{{\omega {C_0}}})}} = - j\frac{1}{{\omega {C_0}}}\frac{{1 - {{(\frac{{{\omega _s}}}{\omega })}^2}}}{{1 - {{(\frac{{{\omega _p}}}{\omega })}^2}}}\]

（ 、Lq、CqL_q、C_q 先串联，然后和 CoC_o 并联）当 ω=ωs\[\omega = {\omega _s}\] 的时候，回路产生串联谐振，电路阻抗为零当 ω=ωp\[\omega = {\omega _p}\]

的时候，回路产生并联谐振，电路阻抗趋无穷当 ω<ωs\[\omega ω>ωp\[\omega > {\omega _p}\] ，

Z=−jx\[Z = - jx\] ，回路呈现容性当 ωs<ω<ωp\[{\omega _s} < \omega < {\omega _p}\] 的时候， Z=+jx\[Z = +jx\] ，回路呈现感性

、ωp、ωs\omega_p、\omega_s差值很小，因此呈现感性的区域非常的窄，呈现感性的阻抗曲线非常陡峭，对稳定频率有利(电容区不宜使用) 考虑动态电阻 的晶体等效阻抗特性Z=[rq+j(ωLq

−1ωCq)](1jωC0)r+j(ωLq−1ωCq−1ωC0)\[Z = \frac{{[{r_q} + j(\omega {L_q} - \frac{1}{{\omega {C_q}}})](\frac{1}{{j\omega {C_0}}})}}{{r + j(\omega {L_q} - \frac{1}{{\omega {C_q}}} - \frac{1}{{\omega {C_0}}})}}\]

并联晶振电路：电路工作在晶体并联谐振频率附近，晶体等效为电感

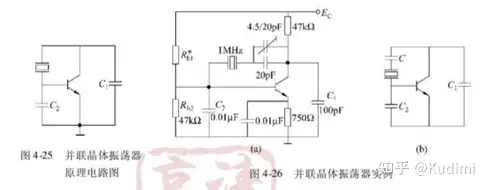
振荡频率的确定： (b)中的谐振回路的等效电路如下：

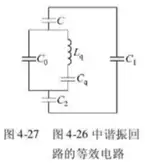
谐振回路的电感就是 LqL_q ，而谐振回路的总电容 CΣC_\Sigma 由 、Cq、CoC_q、C_o和外接电容 、、C、C1、C2C、C_1、C_2组合而成CΣC_\Sigma 的大小为：CΣ=1

Cq+1C0+11C+1C1+1C2\[{C_\Sigma } = \frac{1}{{{C_q}}} + \frac{1}{{{C_0} + \frac{1}{{\frac{1}{C} + \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}}}}}\]

选择电容的时候应该有 C<

那么电路的振荡频率 f0=12πLqCΣ≈12πLq(1Cq+1C0+C)\[{f_0} = \frac{1}{{2\pi \sqrt {{L_q}C{}_\Sigma } }} \approx \frac{1}{{2\pi \sqrt {{L_q}(\frac{1}{{{C_q}}} + \frac{1}{{{C_0} + C}})} }}\]

调节C的大小可以让振荡频率产生微小变动 如果调节C很大近乎无穷 f0≈12πLqCq=fs\[{f_0} \approx \frac{1}{{2\pi \sqrt {{L_q}C{}_q} }} = {f_s}\]

(此时振荡频率取得最小值，近乎晶体的串联谐振频率) 如果调节C非常小，近乎0: f0≈12πLq(CqC0Cq+C0)=fp\[{f_0} \approx \frac{1}{{2\pi \sqrt {{L_q}(\frac{{{C_q}{C_0}}}{{{C_q} + {C_0}}})} }} = {f_p}\]

此时振荡频率取得最大值，近乎晶体的并联谐振频率，只有在附近，晶体a才具有并联谐振回路的特点串联晶振电路： 工作在晶体串联谐振频率附近，晶体近于短路

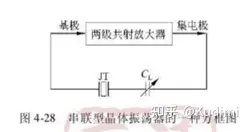
泛音晶振电路 泛音是指石英片振动的机械谐波 泛音是在基频的奇数倍附近，泛音和基频不能并存 并联型泛音晶振电路

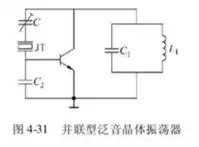
用LC回路替代皮尔斯振荡器的C1，而根据三点式振荡器的原则，当电路正常工作的时候，LC回路应该呈现感性若要晶体工作在5次泛音，则LC回路对其他泛音呈现感性，对5次泛音呈现容性，完成起振 选频回路谐振频率的取值范围。

石英谐振器的频率越高，要求晶片越薄，机械强度越差 一般晶体频率不超过30MHz 为了提高晶振电路的工作频率，可以让电路振荡频率工作在晶体的 谐波频率上(一般在3次到7次谐波)，使用特制的晶体即泛音晶体