Landweber迭代法Landweber Iteration methods）-迭代算法使用while语句

 

基于Landweber迭代法在研究反问题中的广泛应用, Landweber 迭代法用于反问题求解，

它的基本理论、相关结论以及应用，关于Landweber迭代在一些领域,特别是计算机图像重建

等方面的应用已经相当成熟了（个人认知范围），但现在很多期刊上（不乏顶流期刊 eg ：

Inverse problems）仍然有关于Landweber的文献。写该文的目的是为了梳理一下最近的学

习内容。

Landweber 的研究历程

对线性问题(大部分的反问题都可以写成这种形式)

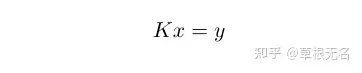
显然当（1）是有限维的，那么K就是一个矩阵，应用代数知识，一方面：若K非奇异，则

其存在唯一的精确解 x=K−1yx=K^{-1}y ,然而，若K非奇异，但K病态（ill-conditioned）此时该显式解

是不稳定的，即它对y中的任何噪声都很敏感。另一方面：若K奇异，此时精确解甚至不存在，

那么如何得到我们想要的解呢?

如果此时有一个解 xkx_{k} 使得

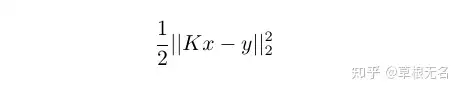
极小（最小），可以认为 xkx_{k} 就是我们想要的解。

考虑其不动点方程

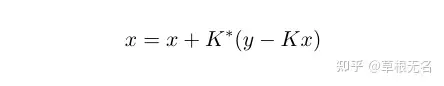
采用迭代算法，则此时的更新（迭代）格式为

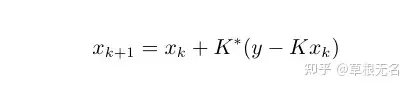
以上就是Landweber在1951年，首次提出该迭代算法并证明其强收敛性，且现在可以将其看作其他通用算法的一个特例。文献记录网盘。

密码: c3pm

此后，Landweber等人改写更新格式为

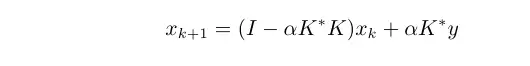
这可以看作是极小化上述二范数的最速下降法。且迭代的步数越多，精度越高，但在实际问题

中，不可能无限迭代。一方面处于计算机存储有限，另一方面，解决问题的时效性得不到满

足。

非线性性和不适定性是反问题最显著的特性。最初对于Landweber 正则化都是通过对初

始条件加以限定或者在特殊的Hilbert Space中 讨 论 其 收 敛 性 与 收 敛 速 度。1994年,

Tautenhanhn 分别讨论了存在扰动误差 δ 和不存在扰动误差两种情况下连续的 Landwebert方法的收敛性。即

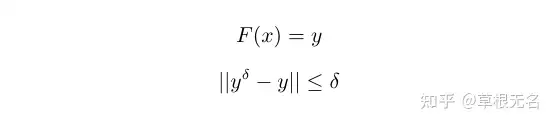
当 δ≠0时,通过求解初值问题

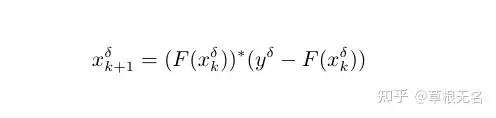
若用步长为1 的 Euler法离散式上式,就是经典的Landweber 迭代法，即

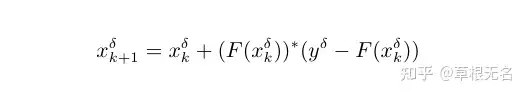
1995,年, Hanke等 人 证 明 了 Landweber迭 代 法 的 收 敛性，且 Scherzer提出了解决非

线性问题的Lanweber迭代法的收敛标准。

1998年, Hettlich对于入射波逆散射问题,研究了通过散射场的远场模式的测量来实现障碍

物的重构,用 Landweber解决反问题的非线性性和不适定性。

2000年，Neubauer推导了Landweber迭代在Hilbert 尺度下的收敛率。并利用有限维空

间估计无限维空间，且给出了有限维估计的收敛性估计。

2001年, Jin等人 主要研究了 Landweber迭代法有限维估计。