1.2 【会动的欧拉公式】欧拉公式可视化-欧拉欧拉动图

 

今天不说别的，聊聊“上帝公式”——欧拉公式的一个简单理解方法。本篇主要是为了让你更好地记住这个公式。

也是为傅里叶级数的复指数展开式（上一篇文章中写的是三角函数展开式）等打个基础。

复数坐标＆向量

像我这样（机械工程）的学生没修过复变函数，导致有时理解相关的概念比较困难，所以我们先整点复数知识。

高中我们就接触过复数坐标，一个复数由实部、虚部组成：z=a+biz = a + bi （有些地方用 j 表示虚数）

这个复数在复数坐标系（实部为横坐标，虚部为纵坐标）中可以表示一个向量：

可以说一个复数即表示一个向量

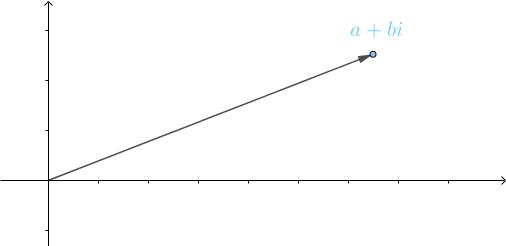
复数系表示向量有很多好处，这里有个很有意思的例子：

将任意复数z1乘以一个虚数i，得到的新的复数z2相当于将z1表示的向量绕原点逆时针旋转90°。（两个向量相互垂直）

z1是个匀速旋转的向量，z2=z1*i

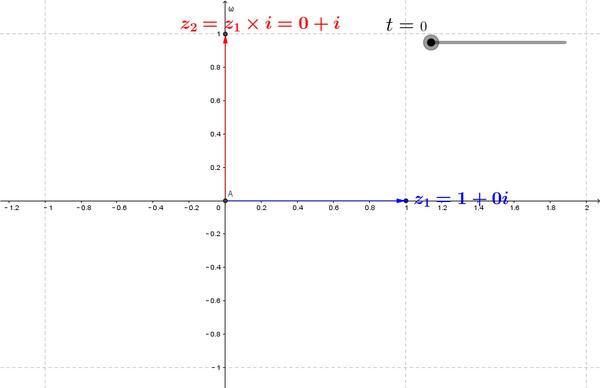
其实，虚数就是因为数学家丰富的想象力而创造的，在笛卡尔坐标系中，某个向量乘-1即是相当于在平面上旋转180°，那么乘根号-1不就是旋转90°吗（？？？牛皮）。

再提一个概念叫“复变函数”：

简单地理解，就是以复数为自变量，因变量也是复数的函数。

A Special Guy

在众多的复变函数中就是有那么一个特别的家伙： f(t)=eitf\left( t \right) = e^{it}

为了便于理解我们可以先将这个函数具象化为一个实例：把函数当作某个向量在复数坐标下的运动方程，认为t是时间，函数的值即是复数坐标系下向量的坐标。

当试图求出他的速度和加速度，我们发现了端倪：

v=df(t)dt=i×eit=i×f(t)v = \frac{df\left( t \right)}{dt} = i \times e^{it} = i \times f\left( t \right)

a=dvdt=d2f(t)dt2=i2×eit=−eit=−f(t)a = \frac{dv}{dt} = \frac{d^{2}f\left( t \right)}{dt^{2}} = i^{2} \times e^{it} = - e^{it} = - f\left( t \right)

① 速度向量垂直于向量本身；

② 加速度向量正好和向量本身方向相反；

此时你灵光乍现( •̀ ω •́ )✧，心中闪出两个曾经学过的东西：

① 速度永远垂直于向量本身，那不就是圆周运动吗？

② 三角函数求两次导后，也是等于本身的负数。

※ 大概是这样一张图 ※

当时间t=π时，向量正好绕半圈，此时函数值为-1，即：

eiπ=−1e^{i\pi} = - 1

圆周运动的横坐标是余弦运动，纵坐标是正弦运动。

所以这里可以拆分成，实部是余弦函数，虚部是正弦函数：

eit=cos⁡t+isin⁡te^{it} = {\cos t} + i{\sin t}

圆周运动的角频率ω不一定为1，考虑加上角频率后：

eiωt=cos⁡ωt+isin⁡ωte^{i\omega t} = {\cos{\omega t}} + i{\sin{\omega t}}

后话

你可以用这个简单的圆周运动来记住欧拉公式。

Of course，欧拉公式不特指运动，变量t也不特指时间，他只是个美丽的数学公式，应用广泛。

对于工程师来说，自变量t大多是指时间。

文章这样的理解方法不能用来严格证明欧拉公式，碰巧看到一个用泰勒级数证明方法：

※ 用泰勒级数证明欧拉公式 ※

下篇我们会利用欧拉公式，由傅里叶级数的三角函数展开式，得到傅里叶级数的复指数展开式。