【通俗易懂】XGBoost从入门到实战，非常详细-套期保值概念、原理与操作原则

Paper：XGBoost - A Scalable Tree Boosting System

如果你从来没学习过 XGBoost，或者不了解这个框架的数学原理。这篇 10000 字的文章一定能帮到你，虽然本文有很多公式，但是仔细读下去一定可以读懂。本文从原理到实战，仔细讲解 XGBoost。如果把这篇博文看懂了，再去读原始文章、看 XGBoost 的 PPT 就会比较轻松了。

有人问我要笔记的 PDF 版本，私我即可。

本篇文章纯手码，参考了很多前辈(比如@李文哲)的讲解，会在文末附上链接。如果这篇文章能帮助到你，来个关注，点赞，收藏吧。 如果有披露，还请留言区指出。

XGBoost 是陈天奇等人开源的一个机器学习项目，高效地实现了 GBDT 算法并进行了算法和工程上的许多改进，被广泛应用在 Kaggle 竞赛及其他许多机器学习竞赛中，并取得了不错的成绩。2015 年 29 组优胜方案中 17 组使用了 XGBoost。

Bagging VS Boosting

Bagging：Leverages unstable base learners that are weak because of overfitting

Boosting: Leverage stable base learners that are weak because of underfitting

Bagging 是 Bootstrap Aggregating 的简称，意思就是再取样 (Bootstrap) 然后在每个样本上训练出来的模型取平均，所以是降低模型的 variance. Bagging 比如 Random Forest 这种先天并行的算法都有这个效果。

Boosting 则是迭代算法，每一次迭代都根据上一次迭代的预测结果对样本进行加权，所以随着迭代不断进行，误差会越来越小，所以模型的 bias 会不断降低。比如 Adaptive Boosting，XGBoost 就是 Boosting 算法。

提升树

给了一个预测问题，张三在此数据上训练出了一个模型 - Model 1，但是效果不怎么好，误差比较大。

问题： 如果我们只能接受去使用这个模型但不能改变模型的架构，那接下来需要怎么做？

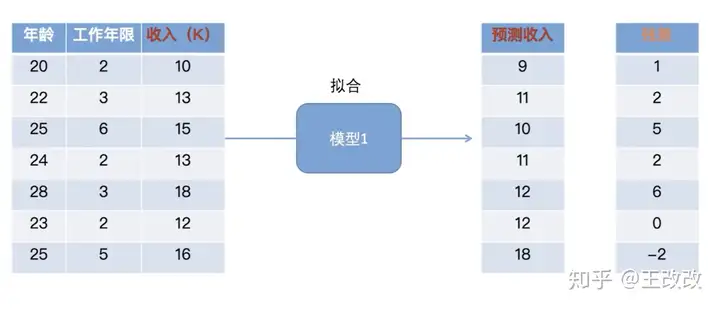
如上图所示，将左侧的数据输入到模型1中，会得到预测收入。预测收入和真实的收入之间的差值记做残差。由于这个模型1有一定的能力，但是能力比较弱，遗留了一些问题。这个残差就能表征这个遗留的问题。

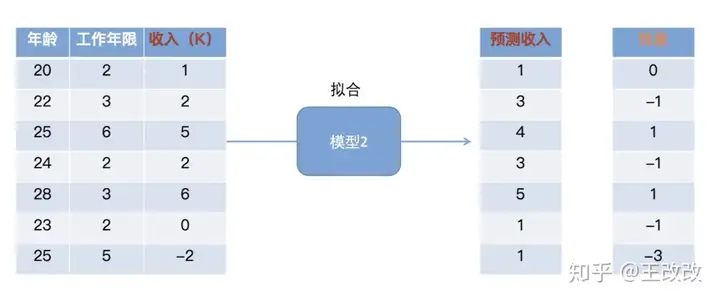
紧接着，再训练一个模型2去预测这些样本，只不过目标值改为刚刚得到的残差。上图所示，预测的结果不再是收入，而是模型1得到的残差。上图中的模型2还会得到残差，但是我们发现第一行样本的残差已经为零了。也就是说第一个样本，通过模型1和模型2能够预测对收入。但是除了第一行，其他的还是有残差的，这时候可以在这基础上训练一个模型3。

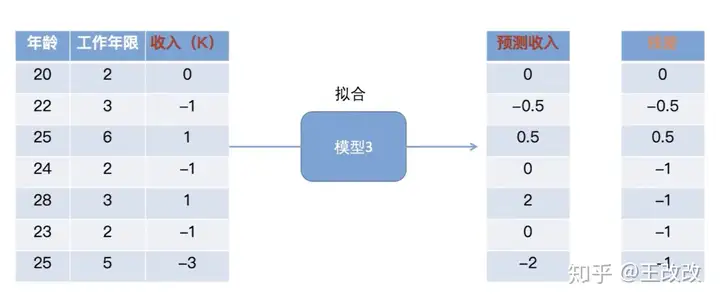
上图所示，在刚刚 模型2得到的残差（准确的说是模型1和模型2共同作用的结果） 的基础上去拟合，得到模型3。这时候的残差可以理解为是前两个模型遗留下来的问题。该模型去预测模型2的残差，我们发现通过前三个模型的预测，得到的残差是上图中最新的残差这一列。

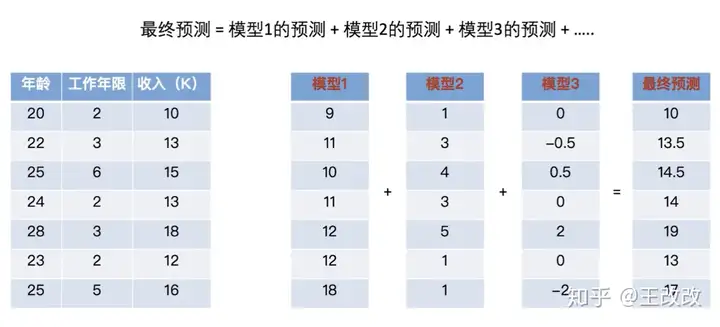
这时候最新的残差都是非常小了，如果能达到我们满意的标准，我们就可以停下。这样我们就得到了三个不同的模型。如下图所示，最终的预测就是三个模型预测的结果和。

具体问题是如何去构造这些模型呢？如何构建目标函数，如何优化？问题可以按照下面的流程去一步步解决：

如何构造目标函数 -> 目标函数直接优化难，如何近似？ -> 如何把树的结构引入到目标函数？-> 仍然难优化，要不要使用贪心算法？

如果看不懂这个流程什么意思，没关系。直接往下读就行了，回过头来看会豁然开朗。

构建目标函数

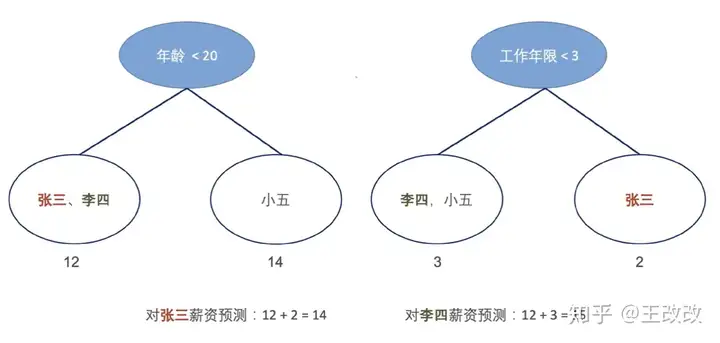
首先举个例子，用多棵树来预测张三、李四的薪资。如下图所示，用年龄这个因素构建的树预测张三的值为12，用工作年限这个因素构建的树张三为2. 两个相加就是对张三薪资的预测：12+2=14。

假设已经训练了 KK 颗树，则对于第 ii 个样本的最终预测值为：

y^i=∑k=1Kfk(xi),fk∈F\widehat{y}_{i}=\sum_{k=1}^{K} f_{k}\left(x_{i}\right), f_{k} \in \mathcal{F} \\

xix_i 是样本的特征，fk(xi)f_{k}\left(x_{i}\right) 是用第 kk 颗树对 xix_i 样本进行预测。将结果加在一起就得到了最终的预测值 y^i\widehat{y}_{i}, 而该样本的真实 label 是 yi{y}_{i} 。这样我们就能构建损失函数了。

构建的目标函数如下：

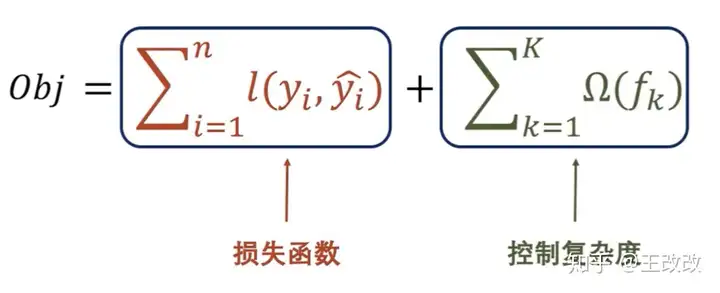
损失函数计算模型预测值和真实值的 loss，其中 ll 是损失函数，可以是 MSE、Cross Entropy 等等。第二项是正则项，来控制模型的复杂度，防止过拟合。这个正则项可以类比 L2 正则。

叠加式的训练

如下图所示，将样本 xix_i 放入第一棵树后，会得到一个预测值 f1(xi)f_1(x_i)，将该样本放入到第二颗树中后会得到 f2(xi)f_2(x_i) 。依次类推。

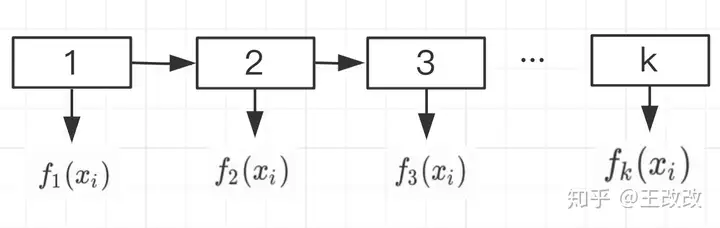
假设给定样本 xix_i 且 y^i<0>=0\hat y_i^{<0>}=0：

y^i⟨0⟩=0y^i⟨1⟩=f1(xi)+y^i⟨0⟩=f1(xi)+0y^i⟨2⟩=f2(xi)+y^i⟨1⟩=f2(xi)+f1(xi)y^i⟨3⟩=f3(xi)+y^i⟨2⟩=f3(xi)+f2(xi)+y^i⟨1⟩=f3(xi)+f2(xi)+f1(xi)...y^i⟨k⟩=f1(xi)+f2(xi)+f3(xi)+...+fk(xi)=∑j=1K−1fj(xi)+fk(xi)=y^i⟨k−1⟩+fk(xi)\begin{aligned} \hat y_i^{\left \langle 0 \right \rangle} &= 0 \\ \hat y_i^{\left \langle 1 \right \rangle} &= f_1(x_i)+\hat y_i^{\left \langle 0 \right \rangle}=f_1(x_i)+0 \\ \hat y_i^{\left \langle 2 \right \rangle} &= f_2(x_i) + \hat y_i^{\left \langle 1 \right \rangle}= f_2(x_i) + f_1(x_i)\\ \hat y_i^{\left \langle 3 \right \rangle} &= f_3(x_i) + \hat y_i^{\left \langle 2 \right \rangle}= f_3(x_i) + f_2(x_i) + \hat y_i^{\left \langle 1 \right \rangle} = f_3(x_i) + f_2(x_i) + f_1(x_i)\\ ...\\ \hat y_i^{\left \langle k \right \rangle} &= f_1(x_i)+f_2(x_i)+f_3(x_i)+...+f_k(x_i) \\ &= \sum_{j=1}^{K-1} f_{j}\left(x_{i}\right)+f_k(x_i) \\ &= \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i) \end{aligned} \\

其中 y^i⟨m⟩\hat y_i^{\left \langle m \right \rangle} 是到第 m 课树为止累加的一个预测结果。通过推断，我们可以知道：y^i⟨k⟩=y^i⟨k−1⟩+fk(xi)\hat y_i^{\left \langle k \right \rangle} = \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i) ，到第 kk 颗树时累加的结果是前 k−1k-1 颗树累计的结果和第 kk 颗树输出的结果总和。有了这个推论，我们再看目标函数：

obj=∑i=1nl(yi,y^i)+∑k=1KΩ(fk)=∑i=1nl(yi,y^i⟨k⟩)+∑k=1KΩ(fk)=∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+∑j=1K−1Ω(fj)+Ω(fK)\begin{aligned} obj &=\sum_{i=1}^{n}l(y_i, \hat y_i)+\sum_{k=1}^{K} \Omega\left(f_{k}\right) \\ &= \sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k \right \rangle})+\sum_{k=1}^{K} \Omega\left(f_{k}\right) \\ &= \sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\sum_{j=1}^{K-1} \Omega\left(f_{j}\right)+\Omega\left(f_{K}\right) \end{aligned} \\

因为最终的预测结果是所有模型（树）累加的结果，所以可以把 y^i\hat y_i 写成 y^i⟨k⟩\hat y_i^{\left \langle k \right \rangle} （到第 k 课树为止累加的一个预测结果）当训练第 KK 颗树时，最下化下面的损失函数：

∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+Ω(fK)\sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\Omega\left(f_{K}\right) \\

相比之下，该式子去掉了 ∑j=1K−1Ω(fj)\sum_{j=1}^{K-1} \Omega\left(f_{j}\right) 这一项，因为训练第 KK 颗树时，该项为常数项，因为在训练第 KK 颗树的时候，前 K−1K-1 颗树的复杂度是已知的，不需要关注前面这些树了。到此为止，我们得出了目标函数：

Minimize:∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+Ω(fK)Minimize:\sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\Omega\left(f_{K}\right) \\

用泰勒级数近似目标函数

这个目标函数是非常复杂的，我们可以用泰勒级数来近似这个目标函数。

目标函数：

Objk=∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+Ω(fK)Obj_k = \sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\Omega\left(f_{K}\right) \\

根据泰勒展开式：

f(x+Δx)≈f(x)+f′(x)⋅Δx+12f′′(x)⋅Δx2f(x+\Delta x)\approx f(x)+f^{\prime}(x) \cdot\Delta x+\frac{1}{2}f^{\prime\prime}(x) \cdot\Delta x^{2} \\

紧接着, 我们把 y^i⟨k−1⟩\hat y_i^{\left \langle k-1 \right \rangle} 视作 xx, 把 fk(xi)f_k(x_i) 视作 Δx\Delta x

f(x)=l(yi,y^i⟨k−1⟩)f(x+Δx)=l(yi,y^i⟨k−1⟩+fk(xi))\begin{aligned} f(x)&=l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}) \\ f(x+\Delta x)&=l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i)) \end{aligned} \\

而根据泰勒展开式可以知道（这里公式可能有点长，但不乱，仔细看就能看懂）：

Objk=∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+Ω(fK)=∑i=1n[l(yi,y^i⟨k−1⟩)+∂y^i⟨k−1⟩l(yi,y^i⟨k−1⟩)+12∂yi^⟨k−1⟩2l(yi,y^i⟨k−1⟩)⋅fk2(xi)]+Ω(fK)\begin{aligned} Obj_k &= \sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\Omega\left(f_{K}\right) \\ &= \sum_{i=1}^{n} [l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})+\partial_{\hat{y}_i^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})+\frac{1}{2}\partial^{2}_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})\cdot f^{2}_k(x_i)]+\Omega\left(f_{K}\right) \end{aligned} \\

当前目标函数是训练第 kk 颗树时的函数，其中 l(yi,y^i⟨k−1⟩)l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}) 项是真实值与到第 k−1k-1 课树为止累加的预测结果的损失，可以看作是已知的，不参与优化的过程。并且 ∂yi^⟨k−1⟩l(yi,y^i⟨k−1⟩)\partial_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}) 和 ∂yi^⟨k−1⟩2l(yi,y^i⟨k−1⟩)\partial^{2}_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})也可以看成已知的。我们假设上式中 ∂yi^⟨k−1⟩l(yi,y^i⟨k−1⟩)=gi\partial_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})=g_i， ∂yi^⟨k−1⟩2l(yi,y^i⟨k−1⟩)=hi\partial^{2}_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})=h_i 故：

Objk=∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+Ω(fK)=∑i=1n[l(yi,y^i⟨k−1⟩)+∂yi^⟨k−1⟩l(yi,y^i⟨k−1⟩)⋅fk(xi)+12∂yi^⟨k−1⟩2l(yi,y^i⟨k−1⟩)⋅fk2(xi)]+Ω(fK)=∑i=1n[l(yi,y^i⟨k−1⟩)+gi⋅fk(xi)+12hi⋅fk2(xi)]+Ω(fK)\begin{aligned} Obj_k &= \sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\Omega\left(f_{K}\right) \\ &= \sum_{i=1}^{n} [l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})+\partial_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})\cdot f_k(x_i)+\frac{1}{2}\partial^{2}_{\hat{y_i}^{\left \langle k-1 \right \rangle}}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})\cdot f^{2}_k(x_i)]+\Omega\left(f_{K}\right) \\ &= \sum_{i=1}^{n} [l(y_i, \hat y_i^{\left \langle k-1 \right \rangle})+g_i \cdot f_k(x_i)+\frac{1}{2}h_i\cdot f^{2}_k(x_i)]+\Omega\left(f_{K}\right) \end{aligned} \\

可以将目标函数简化为如下的形式：

minimize:∑i=1n[gi⋅fk(xi)+12hi⋅fk2(xi)]+Ω(fK)minimize:\sum_{i=1}^{n} [g_i \cdot f_k(x_i)+\frac{1}{2}h_i\cdot f^{2}_k(x_i)]+\Omega\left(f_{K}\right) \\

当训练第 kk 颗树的时候，{hi,gih_i, g_i} 是已知的， hi,gih_i, g_i 可以看作是训练前 k−1k-1 棵树时的残差。由于我们要优化这个目标函数，接下来需要把 fk(xi)f_k(x_i)、Ω(fK)\Omega\left(f_{K}\right) 参数化。

如何用参数表示一颗树

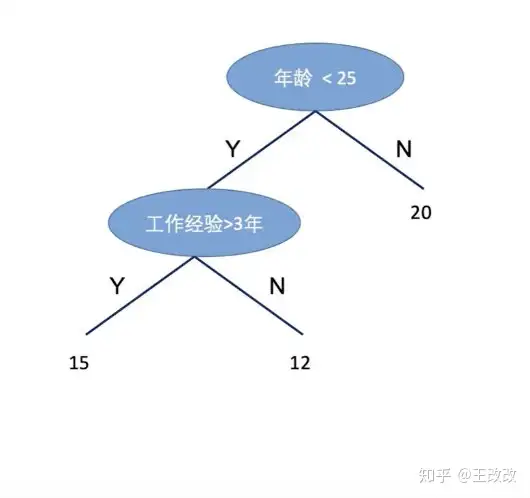
叶子结点的值用 ww 表示，我们假设 15 这个叶节点用 w1w_1 表示，12 这个叶子结点用 w2w_2 表示，20 这个叶子结点用 w3w_3 表示。 W=(w1,w2,w3)=(15,12,20)W=(w_1,w_2,w_3)=(15,12,20) 这里的 WW 就是一个参数。

接下来的目标是把 fk(xi)f_k(x_i)、Ω(fK)\Omega\left(f_{K}\right) 参数化。

fk(xi)f_k(x_i) 是什么呢 ？简单来说，fk(xi)f_k(x_i) 就是第 kk 课树对样本 xix_i 的预测结果。更具体的，就是把第 xix_i 个样本规划到第几个叶子结点上了。

这里定义一个函数 q(x)q(x) :样本 xx 的位置。这里假设第一个叶节点上（即 15 的地方）有样本[1, 3]落在这里 ,第二个节点有样本[4]落在这个地方，样本[2,5]落在了第三个叶子结点处这里 ：

用函数 qq 表示了样本落在了那个位置后，就能用参数表示 fk(xi)f_k(x_i) 了。 样本 xix_i 落在了第 q(xi)q(x_i) 个叶节点上。那么 fk(xi)f_k(x_i) 的预测值就可以用 Wq(xi)W_{q(x_i)} 表示，这样就把 fk(xi)f_k(x_i) 进行了参数化。WW 是一个参数，下角标 q(xi)q(x_i) 表示落在哪个叶子结点上。但是这里下标还是一个函数，需要定义一下：

Ij={i|q(xi)=j}I_j=\{i|q(x_i)=j\} \\

即表示哪些样本 xix_i 落在第 jj 个叶子结点上。举个例子：I1={1,3}I_1=\{1,3\} 表示样本 1，3 落在了第一个节点上。这样进行表示的目的是根据叶节点的位置把样本进行重新的组织。

定义树的复杂度

刚刚把 fk(xi)f_k(x_i) 进行了参数化，接下来的目标是把 Ω(fK)\Omega\left(f_{K}\right) 参数化。

一颗树的复杂度可以通过叶节点个数和 leaf value 。如下式子，其中 TT 为叶节点的个数，第二项表示 leaf value：

Ω(fk)=T+∑j=1T(wj)2\Omega\left(f_{k}\right) = T+\sum_{j=1}^{T}(w_j)^{2} \\

复杂度有两个部分构成的，所以我们可以给每个模块定一个超参数来控制他们：

Ω(fk)=γT+12λ∑t=1T(wt)2\Omega\left(f_{k}\right)=\gamma T+\frac{1}{2} \lambda \sum_{t=1}^{T}\left(w_{t}\right)^{2} \\

新的目标函数

经过上面的一步步的简化，我们把最初的目标函数：

Objk=∑i=1nl(yi,y^i⟨k−1⟩+fk(xi))+Ω(fK)Obj_k = \sum_{i=1}^{n}l(y_i, \hat y_i^{\left \langle k-1 \right \rangle}+f_k(x_i))+\Omega\left(f_{K}\right) \\

简化为了：

∑i=1n[gi⋅fk(xi)+12hi⋅fk2(xi)]+Ω(fK)\sum_{i=1}^{n} [g_i \cdot f_k(x_i)+\frac{1}{2}h_i\cdot f^{2}_k(x_i)]+\Omega\left(f_{K}\right) \\

紧接着，我们根据刚刚定义的参数： WW 叶节点的值，q(xi)q(x_i) 样本 xix_i 落在哪个叶节点上。IjI_j 第 jj 个节点有哪些样本。 fk(xi)f_k(x_i) 的预测值就可以用 Wq(xi)W_{q(x_i)} 表示，可得到：

∑i=1n[gi⋅fk(xi)+12hi⋅fk2(xi)]+Ω(fK)=∑i=1n[gi⋅Wq(xi)+12hi⋅Wq(xi)2]+Ω(fK)=∑i=1n[gi⋅Wq(xi)+12hi⋅Wq(xi)2]+γT+12λ∑t=1T(wt)2\begin{aligned} &\sum_{i=1}^{n} [g_i \cdot f_k(x_i)+\frac{1}{2}h_i\cdot f^{2}_k(x_i)]+\Omega\left(f_{K}\right) \\ &= \sum_{i=1}^{n} [g_i \cdot W_{q(x_i)}+\frac{1}{2}h_i\cdot W_{q(x_i)}^{2}]+\Omega\left(f_{K}\right)\\ &= \sum_{i=1}^{n} [g_i \cdot W_{q(x_i)}+\frac{1}{2}h_i\cdot W_{q(x_i)}^{2}]+\gamma T+\frac{1}{2} \lambda \sum_{t=1}^{T}\left(w_{t}\right)^{2} \end{aligned} \\

紧接着，看下图，假设第一个叶节点上（即 15 的地方）有样本[1, 3]落在这里 ,第二个节点有样本[2]落在这个地方，样本[4,5]落在了第三个叶子结点处这里 ：

所以：

g1⋅Wq(x1)+g2⋅Wq(x2)+g3⋅Wq(x3)+g4⋅Wq(x4)+g5⋅Wq(x5)=g1⋅Wq(x1)+g3⋅Wq(x3)+g2⋅Wq(x2)+g4⋅Wq(x4)+g5⋅Wq(x5)g_1 \cdot W_{q(x_1)}+g_2 \cdot W_{q(x_2)}+g_3 \cdot W_{q(x_3)}+g_4 \cdot W_{q(x_4)}+g_5 \cdot W_{q(x_5)} \\ = g_1 \cdot W_{q(x_1)}+g_3 \cdot W_{q(x_3)}+g_2 \cdot W_{q(x_2)}+g_4 \cdot W_{q(x_4)}+g_5 \cdot W_{q(x_5)} \\

而其中的 g4⋅Wq(x4)+g5⋅Wq(x5)g_4 \cdot W_{q(x_4)}+g_5 \cdot W_{q(x_5)} 又可以表示为（因为样本[4,5]落在了第三个叶子结点处）：

g4⋅Wq(x4)+g5⋅Wq(x5)=∑i∈I3gi⋅W3g_4 \cdot W_{q(x_4)}+g_5 \cdot W_{q(x_5)} = \sum_{i \in I_3}g_i \cdot W_3 \\

因为 Ij={i|q(xi)=j}I_j=\{i|q(x_i)=j\}。所以我们可以进一步构造新的目标函数：

∑i=1n[gi⋅Wq(xi)+12hi⋅Wq(xi)2]+γT+12λ∑t=1T(wt)2=∑j=1T[(∑i∈Ijgi)⋅wj+12(∑i∈Ijhi+λ)⋅(wj)2]+γT=∑j=1T[∑i∈Ijgi⏟constant Gj⋅wj+12(∑i∈Ijhi⏟constant Hj+λ)⋅(wj)2]+γT\begin{aligned} &\sum_{i=1}^{n} [g_i \cdot W_{q(x_i)}+\frac{1}{2}h_i\cdot W_{q(x_i)}^{2}]+\gamma T+\frac{1}{2} \lambda \sum_{t=1}^{T}\left(w_{t}\right)^{2} \\ &=\sum_{j=1}^{T}[(\sum_{i \in I_j}g_i) \cdot w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)\cdot (w_j)^2]+\gamma T\\ &=\sum_{j=1}^{T}[\underbrace{\sum_{i \in I_{j}} g_{i}}_{\text {constant } G_{j}}\cdot w_{j}+\frac{1}{2}(\underbrace{\sum_{i \in I_{j}} h_{i}}_{\text {constant } H_{j}}+\lambda) \cdot (w_{j})^{2}]+\gamma T \end{aligned} \\

这个式子中，∑i∈Ijgi\sum_{i \in I_j}g_i 和 12(∑i∈Ijhi+λ)\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda) 是已知的，分别记做 GjG_j 和 HjH_j。参数是 wjw_j 。所以是一个关于 wjw_j 二次函数求最优解问题。

知识回顾，典型的二次函数：

y=ax2+bx+c(a≠0)y=ax^2+bx+c(a \not= 0) \\

最小点的值为：

(−b2a,4ac−b24a)(-\frac{b}{2a},\frac{4ac-b^2}{4a}) \\

所以，所以当树的结构固定，也就是说 q(x)q(x) 固定的话，在中括号中的最佳 wj∗w_j^{*} 为：

wj∗=−GtHt+λw_j^{*} = -\frac{G_{t}}{H_{t}+\lambda} \\

将 wj∗w_j^{*} 带入到 ∑j=1T[(∑i∈Ijgi)⋅wj+12(∑i∈Ijhi+λ)⋅(wj)2]+γT\sum_{j=1}^{T}[(\sum_{i \in I_j}g_i) \cdot w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)\cdot (w_j)^2]+\gamma T 中可得，当前树结构下的最佳的目标函数值：

-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T \\

当我们的知道了训练第 k 棵树时最小的目标函数值 obj_k^* 后，随意给出一颗树（已知树结构），就能算出该棵树下最小的目标函数值。但是可能会有很多颗树，所以我们需要找到目标函数值最小的那颗树。**那么如何去寻找这棵树呢？**把可能所有的树罗列出来是代价很大的，这时候就需要贪心的方法。

如何寻找树的形状？

我们寻找最小的 obj_k^* ，原来我们有一颗树，我们是能够计算出这棵树最小的目标函数值的。紧接着根据特征进行分割落在叶节点的样本，树结构发生改变，这时候新的树的目标函数值也是能够算出来的。所以，使用贪心的方式，选择新的树目标函数值较小的那颗树。

比如下面这个例子，我们有样本 [1、2、3、4、5、6、7、8]，第一颗树把这些样本分为了两部分，左侧的叶子结点是 [7,8]，右侧节点是 [1,2,3,4,5,6]。

此时我们知道了树的结构，可以根据如下的公式计算出此时树的最小目标函数值：

obj=-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T \\ obj^*_{old}=-\frac{1}{2} [\frac{(g_7+g_8)^2}{h_7+h_8+\lambda}+\frac{(g_1+...+g_6)^2}{h_1+...+h_6+\lambda}]+\gamma 2 \\

紧接着，我们根据新的特征对叶子结点再次进行了分割，得到了如下的树的形状：

此时，得到了新的 Obj_{new}^*:

Obj_{new}^* =-\frac{1}{2} [\frac{(g_7+g_8)^2}{h_7+h_8+\lambda}+\frac{(g_1+g_3+g_5)^2}{h_1+h_3+h_5+\lambda}+\frac{(g_2+g_4+g_6)^2}{h_2+h_4+h_6+\lambda}]+\gamma 3 \\

紧接着计算两颗树最小目标函数值的差：

obj^*_{old} - Obj_{new}^*=\frac{1}{2}[\frac{G_L^{2}}{H_L+\lambda}+\frac{G_R^{2}}{H_R+\lambda}-\frac{(G_R+G_L)^{2}}{H_L+H_R+\lambda}]-\gamma \\ G_L=g_1+g_3+g_5,G_R=g_2+g_4+g_6 \\ H_L=h_1+h_3+h_5,H_R=h_2+h_4+h_6 \\

当 obj^*_{old} - Obj_{new}^* 最大化的时候，便是 Obj_{new}^* 最小的时候。这样我们通过贪心的方式不断构造这棵树，不断扩充这棵树。这里构造树的部分是非常重要的，需要细细品味。如果大概懂了，可以去读原文章哈：XGBoost - A Scalable Tree Boosting System。

实战

实战基于数据集 AllstateClaimsSeverity (Kaggle2016竞赛) ：

官网：https://www.kaggle.com/c/allstate-claims-severity/overview

基于给出的数据预测保险赔偿。给出的训练数据是116列（cat1-cat116）的离散数据和14列（con1-con14）的连续数据。

数据分布

导入依赖

加载数据

观察数据，看看数据是啥样的

输出训练数据，查看数据内容

观察得到：一共有 object 类型属性 116 个，float64 属性15个，int64 属性 1 个，其中 id 是int64，loss 赔偿是 float64.

可以看到此数据已经被处理，均值基本为 0.5。

查看缺失值

大多情况，我们都需要对数据进行缺失值处理。

连续值与离散值

查看离散特征和连续特征个数

离散特征Categorical: 116 features

连续特征Continuous: 14 features

A column of int64:[id]

类别值中属性的个数

正如我们所看到的，大部分的分类特征（72/116）是二值的，绝大多数特征（88/116）有四个值，其中有一个具有326个值的特征（一天的数量？）。

赔偿值

如上图所示，损失值有几个显著的峰值，表示严重事故。这样的数据分布，使得这个功能非常扭曲导致回归表现不佳。

基本上，偏度 度量了实值随机变量的均值分布的不对称性，下面让我们来计算一下loss的偏度：

偏度值比1大，说明数据是倾斜的。不利于数据建模。我们利用对数变换np.log，使倾斜降低。

两种 loss 分布对比：

数据loss对数化之后，是我们喜欢的分布类型。

连续值特征

特征之间的相关性

XGBoost 调参策略

导入依赖

数据预处理

Simple XGBoost Model

首先，我们训练一个基本的xgboost模型，然后进行参数调节通过交叉验证来观察结果的变换，使用平均绝对误差衡量 mean_absolute_error(np.exp(y),np.exp(yhat))。

xgboost 自定义一个数据矩阵类 DMatrix，会在训练开始时，进行一边预处理，从而提高之后每次迭代的效率。

结果衡量方法

Model

XGBoost 参数

使用交叉验证 xgb.cv

上面是我们第一个模型

我们把树模型的数量增加到了100。效果不是很明显。看最后的60次。我们可以看到 测试集仅比训练集高那么一丁点。存在一丁点的过拟合。

不过我们的CV score更低了。接下来，我们改变其他参数。

XGBoost 参数调节

Step 1: 选择一组初始参数 Step 2: 改变 max_depth 和 min_child_weight. Step 3: 调节 gamma 降低模型过拟合风险. Step 4: 调节 subsample 和 colsample_bytree 改变数据采样策略. Step 5: 调节学习率 eta.

按照训练集处理方式，处理我们的测试集

(7.450635, 125546)

(125546,)

Step 1: 基准模型

Step 2: 树的深度与节点权重

这些参数对xgboost性能影响最大，因此，他们应该调整第一。我们简要地概述它们： max_depth: 树的最大深度。增加这个值会使模型更加复杂，也容易出现过拟合，深度3-10是合理的。 min_child_weight: 正则化参数. 如果树分区中的实例权重小于定义的总和，则停止树构建过程。

[4, 5, 6, 7, 8]

网格搜索发现的最佳结果: {max_depth: 8, min_child_weight: 6}, -1187.9597499123447)

Step 3: 调节 gamma去降低过拟合风险

Step 4: 调节样本采样方式 subsample 和 colsample_bytree

在当前的预训练模式的具体案例，我得到了下面的结果： `{colsample_bytree: 0.8, subsample: 0.8}, -1182.9309918891634)

Step 5: 减小学习率并增大树个数

（也可以增大学习率减小树个数）

参数优化的最后一步是降低学习速度，同时增加更多的估计量

First, we plot different learning rates for a simpler model (50 trees):

{eta: 0.2}, -1160.9736284869114 是目前最好的结果, 现在我们把树的个数增加到100

学习率低一些的效果更好

我们继续增大树的个数

总结

可以看到200棵树最好的ETA是0.07。正如我们所预料的那样，ETA和num_boost_round依赖关系不是线性的，但是有些关联。

花了相当长的一段时间优化xgboost. 从初始值: 1219.57. 经过调参之后达到 MAE=1171.77. 我们还发现参数之间的关系ETA和num_boost_round：

100 trees, eta=0.1: MAE=1152.247 200 trees, eta=0.07: MAE=1145.92

`XGBoostRegressor(num_boost_round=200, gamma=0.2, max_depth=8, min_child_weight=6, colsample_bytree=0.6, subsample=0.9, eta=0.07).

xgboost作为kaggle和天池等各种数据比赛最受欢迎的算法之一,从项目中可见调参也是一件很容易的事情,并不复杂,好用精确率高,叫谁谁不用。

参考链接

[1] https://www.zhihu.com/question/26760839/answer/33963551

(2) https://www.bilibili.com/video/BV1si4y1G7Jb