基本初等函数第一篇——幂函数-基本初等函数幂函数图像

 

毕业多年偶然那起考研课本，翻开第一页……这都是些啥鬼画符，突然发现曾经的知识全都还给了老师，顿觉羞愧，不得已重新复习高等数学。然而y=sinx,cosx啥的看着好眼熟，却忘记具体是个啥了。迫不得已只能从高中数学回忆了。像我这种记忆渣，这里纯粹是自学自记录，学霸可以让路~

以下进入正题

基本初等函数：幂函数、指数函数、对数函数、三角函数、反三角函数

幂函数 y=xay=x^{a}

1、公式：y=xay=x^{a}

2、要点：①幂函数的底数是 xx

②幂函数的系数是1 比如 2x22x^{2} 不是幂函数

③指数 aa 可以是任意实数 比如整数、分数、负数等，所以 、x2、x=x12x^{2}、\sqrt{x}=x^{\frac{1}{2}} 、、、x23、1x=x−1、x^{\frac{2}{3}}、\frac{1}{x}=x^{-1} 都是幂函数

④转化形式， aa是负数，与分数转化；

aa是分数，与 x\sqrt{x} 转化，分母根号外，分子根号内

3、特性 幂函数可以写作 y=xmn×(−1)ky=x^{\frac{m}{n}\times(-1)^{k}}

① mm 、 nn 为奇数， kk 为偶数时， y=x35=x35y=x^{\frac{3}{5}}=\sqrt[5]{x^{3}} ，定义域为R，是奇函数

② mm 、 nn 为奇数， kk 为奇数时， y=x−35=1x35y=x^{-\frac{3}{5}}=\frac{1}{\sqrt[5]{x^{3}}} ，定义域为 (−∞,0)(0,+∞)(-\infty,0)(0,+\infty) ，是奇函数

③ mm 为奇数、 nn 为偶数， kk 为偶数时， y=x38=x38y=x^{\frac{3}{8}}=\sqrt[8]{x^{3}} ，定义域为 [0,+∞)[0,+\infty) ，是非奇非偶函数

④ mm 为奇数、 nn 为偶数， kk 为奇数时， y=x−38=1x38y=x^{-\frac{3}{8}}=\frac{1}{\sqrt[8]{x^{3}}} ，定义域为 (0,+∞)(0,+\infty) ，是非奇非偶函数

⑤ mm 为偶数、 nn 为奇数， kk 为偶数时， y=x47=x47y=x^{\frac{4}{7}}=\sqrt[7]{x^{4}} ，定义域为R，是偶函数

⑥ mm为偶数、 nn 为奇数， kk 为奇数时， y=x−47=1x47y=x^{-\frac{4}{7}}=\frac{1}{\sqrt[7]{x^{4}}}

，定义域为 R，是偶函数

4、图像

①，a=1，y=x1a=1，y=x^{1}

a=1时，定义域{-∞,+∞}

② ，a=0，y=x0a=0，y=x^{0}

a=1时，定义域(-∞,0),(0,+∞)

除了以上两种特殊图形，请先记住以下表格

9种通用幂函数图像

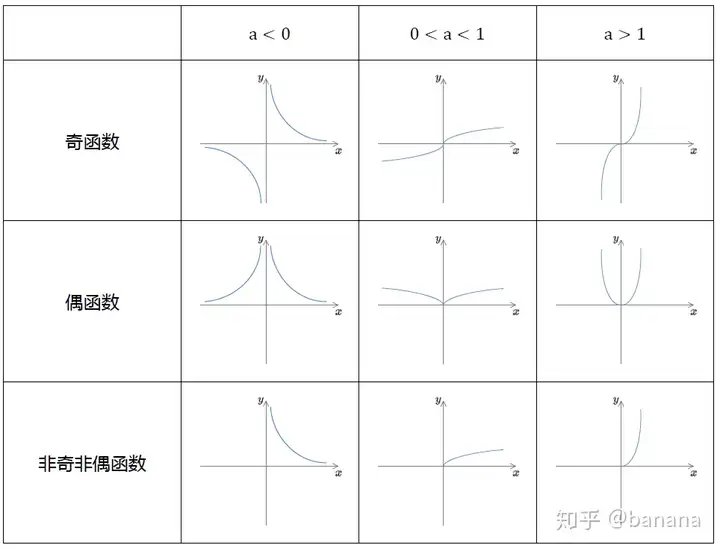
记忆思路

1.看 aa 属于哪个区间：

第一象限内，a<0a<0 ,图像递减； 0<a<10<a<1 ，图像缓慢递增； 1 ">a>1a>1 ,图像快速递增

2.判断函数奇偶性

在1的基础上，偶函数，关于y轴对称；奇函数，关于原点对称；非奇非偶函数，只有第一象限图形

举好几个栗子：

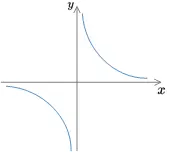
1）y=x−1y=x^{-1}

① a<0a<0 ,所以函数曲线在第一象限呈递减姿态

② y=x−1=1xy=x^{-1} = \frac{1}{x} ,属于奇函数，所以是关于原点对称

因此符合图形

a&amp;lt;0，且为奇函数

2）y=x23y=x^{\frac{2}{3}}

① 0<a<10<a<1 ,所以函数曲线在第一象限呈缓慢递增姿态

② y=x23=x23y=x^{\frac{2}{3}} = \sqrt[3]{x^{2}} ,属于偶函数，所以是关于y轴对称

因此符合图形

0&amp;lt;a&amp;lt;1，且为偶函数

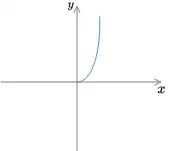
2）y=x32y=x^{\frac{3}{2}}

① 1">a>1a>1 ,所以函数曲线在第一象限呈快速递增姿态

② y=x32=x3y=x^{\frac{3}{2}} = \sqrt{x^{3}} ,属于非奇非偶函数（定义域为(0,+∞)），所以只有第一象限

因此符合图形

a&amp;gt;1，且非奇非偶函数