高中数学：指数函数、对数函数、幂函数-指数函数幂函数对数函数增长的比较

2023-08-11 18:14:49

首先介绍一下 $n$ n 次方根。对于正偶数 $n$ n，非负实数 $x$ x，定义 $xn$ \sqrt[n]{x} 为非负实数且满足 $(xn)n=x$ (\sqrt[n]{x})^n=x。例如，因为 $24=16$ 2^4=16，所以 $164=2$ \sqrt[4]{16}=2。若 $x$ x 为负数， $xn$ \sqrt[n]{x} 没有定义，因为 $n$ n 为正偶数时，一个实数的 $n$ n 次方必然是非负实数。 $n=2$ n=2 时，这就是常见的算术平方根。对于正奇数 $n$ n，实数 $x$ x，定义 $xn$ \sqrt[n]{x} 为满足 $(xn)n=x$ (\sqrt[n]{x})^n=x 的实数。例如，因为 $(-3)3=-27$ (-3)^3=-27，所以 $-273=-3$ \sqrt[3]{-27}=-3。注意此时 $xn$ \sqrt[n]{x} 对所有实数都有定义，且 $f(x)=xn$ f(x)=\sqrt[n]{x} 为奇函数。这是因为 $n$ n 为正奇数时，一个实数的 $n$ n 次方可以取遍所有实数，且相反数的 $n$ n 次方等于 $n$ n 次方的相反数。

数学中，我们经常希望把一个运算推广到更大的范围，所以我们接下来把幂运算 $ab$ a^b 的指数 $b$ b 从整数范围推广到实数范围。

若 $b$ b 为整数， $ab$ a^b 就是 $b$ b 个 $a$ a 相乘。若 $b$ b 不是整数，例如 $b=12$ b=\frac{1}{2} 时，我们不知道 $12$ \frac{1}{2} 个 $a$ a 相乘是什么意思，但我们先忽略这个问题，仍然试图把 $a12$ a^{\frac{1}{2}} 理解为 $12$ \frac{1}{2} 个 $a$ a 相乘。那么， $12$ \frac{1}{2} 个 $a$ a 相乘，再乘以 $12$ \frac{1}{2} 个 $a$ a 相乘，乘了两个 $12$ \frac{1}{2} 个 $a$ a 相乘，这就应当得到 $12+12=1$ \frac{1}{2}+\frac{1}{2}=1 个 $a$ a 相乘，而一个 $a$ a 相乘就是 $a$ a！所以， $a12$ a^{\frac{1}{2}} 应当满足 $a12\cdota12=a$ a^{\frac{1}{2}}\cdot a^{\frac{1}{2}}=a，所以 $a12=\pma$ a^{\frac{1}{2}}=\pm \sqrt{a}。这样一来， $a12$ a^{\frac{1}{2}} 有两个值，这是个问题，不过一般规定 $a12=a$ a^{\frac{1}{2}}=\sqrt{a}。这样，我们就定义了 $a12$ a^{\frac{1}{2}}。

同理， $b=pq$ b=\frac{p}{q}（ $p\inZ$ p\in \mathbb{Z}， $q\inN*$ q\in \mathbb{N^*}）时，乘 $q$ q 次 $pq$ \frac{p}{q} 个 $a$ a 相乘就应当得到 $p$ p 个 $a$ a 相乘，而这就是 $ap$ a^p，所以 $(apq)q=ap$ \left(a^{\frac{p}{q}}\right)^q=a^p，所以 $apq=apq$ a^{\frac{p}{q}}=\sqrt[q]{a^p}。这样， $b$ b 为有理数时， $ab$ a^b 就都有定义了。

接下来考虑 $b$ b 为无理数的情况，例如 $a=2$ a=2， $b=2$ b=\sqrt{2}。此时之前的方法不管用了，因为乘几次 $2$ \sqrt{2} 个 $2$ 2 相乘都达不到整数个 $2$ 2 相乘。但是，因为 $2=1.41421...\approx1410$ \sqrt{2}=1.41421...\approx \frac{14}{10}，所以应当有 $22\approx21410=21410=2.63901...$ 2^{\sqrt{2}}\approx 2^{\frac{14}{10}}=\sqrt[10]{2^{14}}=2.63901...。我们可以做的更好：因为 $2\approx141100$ \sqrt{2}\approx \frac{141}{100}，所以 $22\approx2141100=2141100=2.65737...$ 2^{\sqrt{2}}\approx 2^{\frac{141}{100}}=\sqrt[100]{2^{141}}=2.65737...。类似， $22\approx214141000=214141000=2.66474...$ 2^{\sqrt{2}}\approx 2^{\frac{1414}{1000}}=\sqrt[1000]{2^{1414}}=2.66474...， $22\approx21414210000=21414210000=2.66511...$ 2^{\sqrt{2}}\approx 2^{\frac{14142}{10000}}=\sqrt[10000]{2^{14142}}=2.66511...。我们取 $2$ \sqrt{2} 的小数位越来越多，估计 $22$ 2^{\sqrt{2}} 的精度就越来越高。事实上，我们可以这样定义 $22$ 2^{\sqrt{2}}： $21410$ 2^{\frac{14}{10}}， $2141100$ 2^{\frac{141}{100}}， $214141000$ 2^{\frac{1414}{1000}}， $21414210000$ 2^{\frac{14142}{10000}}， $...$ ... 这一列数逼近的值就是 $22$ 2^{\sqrt{2}}（这个逼近有更准确的定义，但不那么好理解，这里暂不讨论）。取更多的小数位，可得 $22$ 2^{\sqrt{2}} 的精确值为 $2.66514...$ 2.66514...，和我们前面的估计值很接近了，前四个小数位都相同。

同理可以定义 $b$ b 为无理数时 $ab$ a^b 的值。 $a=3$ a=3， $b=π$ b=\pi 时， $3π$ 3^\pi 就是 $33110$ 3^\frac{31}{10}， $3314100$ 3^\frac{314}{100}， $331411000$ 3^\frac{3141}{1000}， $33141510000$ 3^\frac{31415}{10000}， $...$ ... 这一列数逼近的值。这样，对于所有实数 $b$ b， $ab$ a^b 都有定义了。可以证明，这样定义的 $ab$ a^b 满足整数次幂的绝大多数运算性质。

我们再考虑 $a$ a

的取值范围：

（1）

b

b 为有理数时，设

b=pq

b=\frac{p}{q}，这里

p

p、

q

q 为互质的整数，且 0">

q>0

q>0

。

（I）

q

q 为奇数，且 0">

p>0

p>0 时，

ab=apq

a^b=\sqrt[q]{a^p} 对所有实数

a

有定义；

（II）

q

q 为奇数，且

p\leq0

p\le 0 时，

ab=apq

a^b=\sqrt[q]{a^p} 对所有非零实数

a

有定义；

（III）

q

q 为偶数，且 0">

p>0

p>0 时，由

p

p 和

q

q 互质，

p

p 必然为奇数，所以

ab=apq

a^b=\sqrt[q]{a^p} 只对

a\geq0

a\ge 0 有定义（

a<span><span class=

a<0 时

a^p<span><span class=

a^p<0

）；

（IV）

q

q 为偶数，且

p\leq0

p\le 0 时，和情况（III）类似，可知

ab=apq

a^b=\sqrt[q]{a^p} 只对 0">

a>0

a>0

有定义；

（2）

b

b 为无理数时，一般认为

ab

a^b 在 0">

b>0

b>0 时只对

a\geq0

a\ge 0 有定义，在

b\leq0

b\le 0 时只对 0">

a>0

a>0 有定义。

幂函数与指数函数

我们把形如 $f(x)=xα$ f(x)=x^\alpha（ $α$ \alpha 为常数）的函数叫做幂函数。不同的 $α$ \alpha 会产生性质不同的幂函数：

（1） $α$ \alpha 为分子为偶数，分母为奇数的正有理数时（包括正偶数）， $f(x)$ f(x) 为定义在 $R$ \mathbb{R} 上的偶函数，其值域为 $[0,+\infty)$ [0,+\infty)，在 $(-\infty,0)$ (-\infty,0) 上单调递减，在 $(0,+\infty)$ (0,+\infty)

上单调递增；

（2）

α

\alpha 为分子、分母都为奇数的正有理数时（包括正奇数），

f(x)

f(x) 为定义在

R

\mathbb{R} 上的奇函数，其值域为

R

\mathbb{R}，在

R

\mathbb{R}

上单调递增；

（3）

α

\alpha 为分子为偶数，分母为奇数的负有理数时（包括负偶数），

f(x)

f(x) 为定义在

(-\infty,0)\cup(0,+\infty)

(-\infty,0)\cup (0,+\infty) 上的偶函数，其值域为

(0,+\infty)

(0,+\infty)，在

(-\infty,0)

(-\infty,0) 上单调递增，在

(0,+\infty)

(0,+\infty) 上单调递减，其图象有两条渐近线：

x

x 轴和

y

轴；

（4）

α

\alpha 为分子、分母都为奇数的负有理数时（包括负奇数），

f(x)

f(x) 为定义在

(-\infty,0)\cup(0,+\infty)

(-\infty,0)\cup (0,+\infty) 上的奇函数，其值域为

(-\infty,0)\cup(0,+\infty)

(-\infty,0)\cup (0,+\infty)，在

(-\infty,0)

(-\infty,0) 和

(0,+\infty)

(0,+\infty) 上单调递减，其图象有两条渐近线：

x

x 轴和

y

轴；

（5）

α

\alpha 为正无理数或分母为偶数的正有理数时，

f(x)

f(x) 为定义在

[0,+\infty)

[0,+\infty) 上的增函数，其值域为

[0,+\infty)

[0,+\infty)

；

（6）

α

\alpha 为负无理数或分母为偶数的负有理数时，

f(x)

f(x) 为定义在

(0,+\infty)

(0,+\infty) 上的减函数，其值域为

(0,+\infty)

(0,+\infty)，图象有两条渐近线：

x

x 轴和

y

轴；

（7）

α=0

\alpha=0 时，

f(x)

f(x) 定义域为

(-\infty,0)\cup(0,+\infty)

(-\infty,0)\cup (0,+\infty)，且在定义域内恒有

f(x)=1

f(x)=1。

此外，所有幂函数的图象都通过点 $(1,1)$ (1,1)，因为 $1$ 1 的任意实数次幂都是 $1$ 1。

不同幂函数的图象如下图所示：

Image

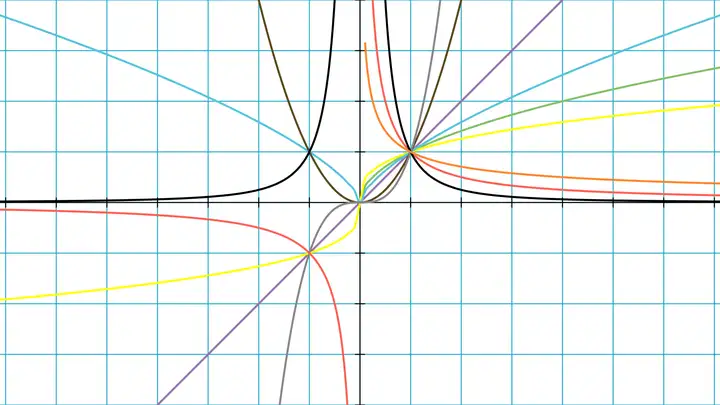
我们把形如 $f(x)=ax$ f(x)=a^x（ $a$ a 为常数，且 0"> $a>0$ a>0， $a\neq1$ a\neq 1）的函数叫做指数函数。显然，所有指数函数的定义域为 $R$ \mathbb{R}，值域为 $(0,+\infty)$ (0,+\infty)。若 1"> $a>1$ a>1， $f(x)$ f(x) 在 $R$ \mathbb{R} 上单调递增（因为 $a$ a 越乘越大）；若 $a $a>0$ a>0 的零次方都是 $1$ 1。

不同指数函数的图象如下图所示：

Image

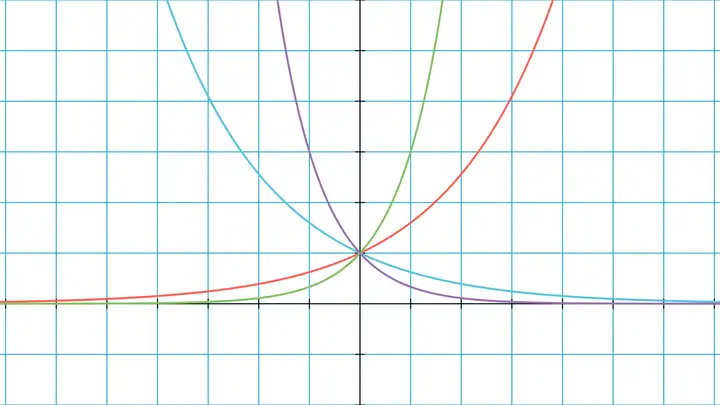
可以发现， $ax$ a^x 的函数图象与 $(1a)x$ \left(\frac{1}{a}\right)^x 的函数图象关于 $y$ y 轴对称。这是因为从 $1$ 1 开始乘 $x$ x 个 $a$ a 就相当于除 $x$ x 个 $1a$ \frac{1}{a}，也就是乘 $-x$ -x 个 $1a$ \frac{1}{a}。

一个增长率恒定的量的变化过程可以用指数函数描述。例如，若A市2000年的人口为 $300$ 300 万人，在此后一段时间内，A市人口每年增长 $2%$ 2\%，则2001年，A市人口为 $300\cdot1.02$ 300\cdot 1.02 万人，2002年，A市人口为 $300\cdot1.02\cdot1.02=300\cdot1.022$ 300\cdot 1.02\cdot 1.02=300\cdot 1.02^2 万人，2003年，A市人口为 $300\cdot1.022\cdot1.02=300\cdot1.023$ 300\cdot 1.02^2\cdot 1.02=300\cdot 1.02^3 万人， $...$ ...。可以发现，在 $y$ y 年，A市人口为 $300\cdot1.02y-2000$ 300\cdot 1.02^{y-2000}，是一个指数函数乘以一个常数（这里常数为 $300\cdot1.02-2000$ 300\cdot 1.02^{-2000}）。

对数函数

若实数 $a,x,y$ a,x,y 满足 $ax=y$ a^x=y 且 0"> $a>0$ a>0， $a\neq1$ a\neq 1，那么我们称“以 $a$ a 为底 $y$ y 的对数为 $x$ x”， $a$ a 叫做对数的“底”， $y$ y 叫做对数的“真数”，记作 $logay=x$ \log _ay=x，形如 $f(x)=logax$ f(x)=\log_a x（0,a\neq 1"> $a>0,a\neq1$ a>0,a\neq 1）的函数叫做对数函数。

就像除法是乘法的逆运算，对数可以理解为指数的逆运算。换句话说，对数 $logax$ \log_a x 回答了这个问题： $a$ a 的多少次方等于 $x$ x？例如，因为 $33=27$ 3^3=27， $(15)2=125$ \left(\frac{1}{5}\right)^2=\frac{1}{25}， $2π\approx8.825$ 2^\pi \approx 8.825，所以 $log327=3$ \log_3 27=3， $log15125=2$ \log_{\frac{1}{5}} \frac{1}{25}=2， $log28.825\approxπ$ \log_2 8.825\approx \pi。因为正数 $a$ a 的多少次方都还是正数，所以 $logax$ \log_a x 只对 0"> $x>0$ x>0 有定义。

经常把 $log10x$ \log_{10} x 叫做 $x$ x 的常用对数，记作 $lgx$ \lg x，因为工程中以 $10$ 10 为底的对数比较常用。经常把 $logex$ \log_e x 叫做 $x$ x 的自然对数，记作 $lnx$ \ln x，这里 $e=2.71828...$ e=2.71828... 是一个无理常数。这个对数怎么就自然了呢？学了导数就会发现， $lnx$ \ln x 有很多很好的性质，例如它的图象在 $x=1$ x=1 处的切线斜率恰好为 $1$ 1，1"> $a>1$ a>1 时 $lna$ \ln a 恰好等于 $y=1x$ y=\frac{1}{x} 在 $x=1$ x=1 到 $x=a$ x=a 一段下方区域的面积等。

对数函数的图象如下图所示。所有对数函数的定义域都是 $(0,+\infty)$ (0,+\infty)，值域都是 $R$ \mathbb{R}。这是因为 $logax$ \log_a x 回答了 $a$ a 的多少次方等于 $x$ x，而 $a$ a 的任何实数次方都有定义，且可以取到任何正实数，所以 $logax$ \log_a x 在 0"> $x>0$ x>0 时都有定义，且可以取任何实数。所有对数函数的图象都过定点 $(1,0)$ (1,0)，这是因为任何正实数 $a$ a 的零次方等于 $1$ 1，所以满足 $ax=1$ a^x=1 的实数 $x$ x 恒为 $0$ 0，即 $loga1=0$ \log_a 1=0。 $0<a $a>1$ a>1 时， $f(x)$ f(x) 在其定义域内单调递增。这是因为 1"> $a>1$ a>1 时， $ax$ a^x 单调递增，所以 $y$ y 越大，满足 $ax=y$ a^x=y 的实数 $x$ x 越大，即 $logay$ \log_a y 越大，即 $f(x)=logax$ f(x)=\log_a x 在其定义域内单调递增（ $0<a<span class=$ 0<a<1 的情况请读者自行补充）。

Image

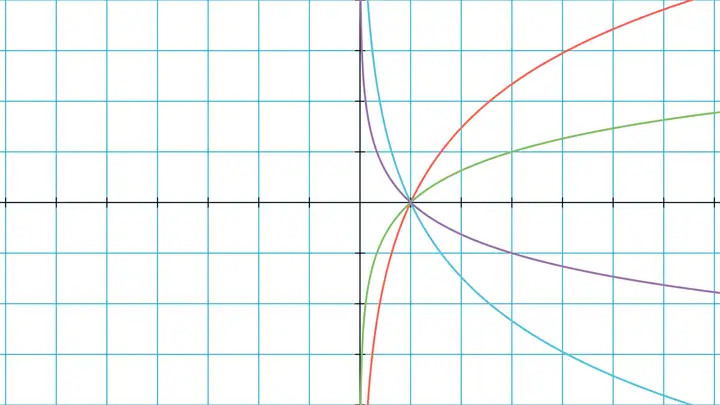
如果把对数函数和指数函数的图象画在一起，还能发现对数函数 $f(x)=logax$ f(x)=\log_a x 和指数函数 $g(x)=ax$ g(x)=a^x 的图象关于直线 $y=x$ y=x 对称。设 $f(x)=logax$ f(x)=\log_a x 的图象上有一点 $(x0,y0)$ (x_0,y_0)，那么 $y0=logax0$ y_0=\log_a x_0。然后由对数函数的定义， $ay0=x0$ a^{y_0}=x_0，即点 $(y0,x0)$ (y_0,x_0) 在 $g(x)=ax$ g(x)=a^x 的图象上。同理，若 $g(x)$ g(x) 图象上有一点 $(x1,y1)$ (x_1,y_1)，那么点 $(y1,x1)$ (y_1,x_1) 就在 $f(x)$ f(x) 图象上。而 $(x,y)$ (x,y) 和 $(y,x)$ (y,x) 关于 $y=x$ y=x 对称，这就说明了 $f(x)$ f(x) 和 $g(x)$ g(x) 的图象关于 $y=x$ y=x 对称。

Image

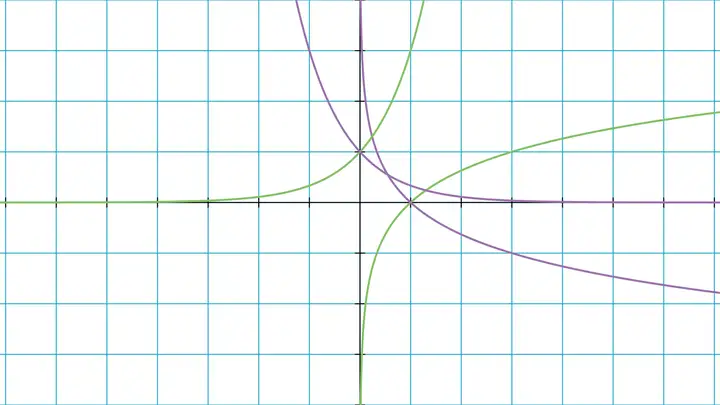
接下来研究对数运算的性质。虽然 $ax$ a^x 中 $x$ x 不一定为整数，但为了方便从直观上解释，我们接下来仍然把 $ax$ a^x 理解为 $x$ x 个 $a$ a 相乘（读者可以自行推导对数运算性质的代数证明）。

0"> $x,y>0$ x,y>0 时， $logax$ \log_a x 是几个 $a$ a 相乘得到 $x$ x， $logay$ \log_a y 是几个 $a$ a 相乘得到 $y$ y。我们乘 $logax$ \log_a x 个 $a$ a 得到 $x$ x，在此基础上再乘 $logay$ \log_a y 个 $a$ a 就能得到 $xy$ xy。这相当于乘了 $logax+logay$ \log_a x+\log_a y 个 $a$ a 得到了 $xy$ xy，而 $logaxy$ \log_a xy 就是几个 $a$ a 相乘得到 $xy$ xy，所以 $logaxy=logax+logay$ \log_a xy=\log_a x+\log_a y。然后，我们乘 $logax$ \log_a x 个 $a$ a 得到 $x$ x，在此基础上再除 $logay$ \log_a y 个 $a$ a 就能得到 $xy$ \frac{x}{y}。因为除 $logay$ \log_a y 个 $a$ a 就相当于乘 $-logay$ -\log_a y 个 $a$ a，所以这相当于乘了 $logax-logay$ \log_a x-\log_a y 个 $a$ a 得到了 $xy$ \frac{x}{y}，所以 $logaxy=logax-logay$ \log_a \frac{x}{y}=\log_a x-\log_a y。

0"> $x>0$ x>0 时，因为 $xk$ x^k 是 $k$ k 个 $x$ x 相乘，而 $x$ x 是 $logax$ \log_a x 个 $a$ a 相乘，所以 $xk$ x^k 就是 $k$ k 个 $logax$ \log_a x 个 $a$ a 相乘，即 $klogax$ k\log_a x 个 $a$ a 相乘。所以 $logaxk=klogax$ \log_a x^k=k\log_a x。特别地， $k=-1$ k=-1 时，我们得到 $loga1x=-logax$ \log_a \frac{1}{x}=-\log_a x。

注意， $x,y\inR$ x,y\in \mathbb{R} 时，不一定有 $logaxy=logax+logay$ \log_a xy=\log_a x+\log_a y，例如 $x=y=-1$ x=y=-1 时， $logaxy=loga1=0$ \log_a xy=\log_a 1=0，而 $logax+logay=2loga-1$ \log_a x+\log_a y=2\log_a -1 没有定义。类似不一定有 $logaxk=klogax$ \log_a x^k=k\log_a x。

$a$ a 是 $logca$ \log_c a 个 $c$ c 相乘， $b$ b 是 $logcb$ \log_c b 个 $c$ c 相乘。那么， $logcalogcb$ \frac{\log_c a}{\log_c b} 个 $b$ b 相乘，就是 $logcalogcb$ \frac{\log_c a}{\log_c b} 个 $logcb$ \log_c b 个 $c$ c 相乘，就是 $logca$ \log_c a 个 $c$ c 相乘，而这就是 $a$ a。而 $logba$ \log_b a 就是多少个 $b$ b 相乘得到 $a$ a，所以 $logba=logcalogcb$ \log_b a=\frac{\log_c a}{\log_c b}。这叫做对数的换底公式。

在 $x$ x 很大时，指数函数 $ax$ a^x（1"> $a>1$ a>1）会超过任何幂函数 $xα$ x^\alpha（0"> $α>0$ \alpha>0），而任何幂函数 $xα$ x^\alpha（0"> $α>0$ \alpha>0）都会超过对数函数 $logax$ \log_a x（1"> $a>1$ a>1）。可以这样理解：为了使 $ax$ a^x 翻倍，我们把 $x$ x 加上常数 $loga2$ \log_a 2 就行了；为了使 $xα$ x^\alpha 翻倍，我们需要把 $x$ x 乘上常数 $21α$ 2^{\frac{1}{\alpha}}；而为了使 $logax$ \log_a x 翻倍，我们需要把 $x$ x 平方。但这不意味着 $x$ x 取任何值时，x^\alpha"> $ax>xα$ a^x>x^\alpha，\log_a x"> $xα>logax$ x^\alpha>\log_a x。例如，指数函数 $1.01x$ 1.01^x 在 $x$ x 比较小时要小于幂函数 $x100$ x^{100}，对数函数 $log1.01x$ \log_{1.01} x 在 $x$ x 比较小时要大于幂函数 $x1100$ x^{\frac{1}{100}}。到 $x=117300$ x=117300 左右， $1.01x$ 1.01^x 才会超过 $x100$ x^{100}；到 $x=8.566\times10506$ x=8.566\times 10^{506} 左右， $x1100$ x^{\frac{1}{100}} 才会超过 $log1.01x$ \log_{1.01} x。

指数、对数的运算

对于含指数、对数的表达式化简的问题，就：

（1）把所有对数用换底公式化为底相同的对数。这个底取多少都行，下文一律使用自然对数 $lnx$ \ln x

。

（2）把所有指数的底数 $a$ a 化为 $clogca$ c^{\log_c a}，这里 $c$ c 为之前使用的对数的底，再把 $logca$ \log_c a 乘到指数上来

。

（3）把所有对数的真数表示为若干个质数的幂的乘积，由此把所有对数化为关于若干个质数的对数的表达式

。

（4）把在指数上的所有对数用对数的性质化为一个对数，从而消掉指数

。

（5）把每个质数的对数看作没有任何关系的变量，进行化简。

例1.（福建长汀一中2022月考）计算： $(lg2)2+lg20\timeslg5-27log32+log34\timeslog29$ (\lg 2)^2+\lg 20\times \lg 5-27^{\log_3 2}+\log_3 4\times \log_2 9。

$（第一步）（第二步）（第三步）（第三步）（第四步）（第四步）（第四步）（第五步）（第五步）（第五步） (lg2)2+lg20\timeslg5-27log32+log34\timeslog29=(ln2ln10)2+ln20ln10\cdotln5ln10-27ln2ln3+ln4ln3\cdotln9ln2（第一步）=(ln2ln10)2+ln20ln10\cdotln5ln10-eln27\cdotln2ln3+ln4ln3\cdotln9ln2（第二步）=(ln2ln2\cdot5)2+ln22\cdot5ln2\cdot5\cdotln5ln2\cdot5-eln33\cdotln2ln3+ln22ln3\cdotln32ln2（第三步）=(ln2ln2+ln5)2+2ln2+ln5ln2+ln5\cdotln5ln2+ln5-e3ln3\cdotln2ln3+2ln2ln3\cdot2ln3ln2（第三步）=(ln2ln2+ln5)2+2ln2+ln5ln2+ln5\cdotln5ln2+ln5-e3ln2+2ln2ln3\cdot2ln3ln2（第四步）=(ln2ln2+ln5)2+2ln2+ln5ln2+ln5\cdotln5ln2+ln5-eln8+2ln2ln3\cdot2ln3ln2（第四步）=(ln2ln2+ln5)2+2ln2+ln5ln2+ln5\cdotln5ln2+ln5-8+2ln2ln3\cdot2ln3ln2（第四步）=(ln2)2+ln5(2ln2+ln5)(ln2+ln5)2-8+4（第五步）=(ln2)2+2ln2\cdotln5+(ln5)2(ln2)2+2ln2\cdotln5+(ln5)2-4（第五步）=-3（第五步）$ \begin{align*} &(\lg 2)^2+\lg 20\times \lg 5-27^{\log_3 2}+\log_3 4\times \log_2 9\\ &=\left(\frac{\ln 2}{\ln 10}\right)^2+\frac{\ln 20}{\ln 10}\cdot \frac{\ln 5}{\ln 10}-27^{\frac{\ln 2}{\ln 3}}+\frac{\ln 4}{\ln 3}\cdot \frac{\ln 9}{\ln 2}&（第一步）\\ &=\left(\frac{\ln 2}{\ln 10}\right)^2+\frac{\ln 20}{\ln 10}\cdot \frac{\ln 5}{\ln 10}-e^{\ln 27\cdot \frac{\ln 2}{\ln 3}}+\frac{\ln 4}{\ln 3}\cdot \frac{\ln 9}{\ln 2}&（第二步）\\ &=\left(\frac{\ln 2}{\ln 2\cdot 5}\right)^2+\frac{\ln 2^2\cdot 5}{\ln 2\cdot 5}\cdot \frac{\ln 5}{\ln 2\cdot 5}-e^{\ln 3^3\cdot \frac{\ln 2}{\ln 3}}+\frac{\ln 2^2}{\ln 3}\cdot \frac{\ln 3^2}{\ln 2}&（第三步）\\ &=\left(\frac{\ln 2}{\ln 2+\ln 5}\right)^2+\frac{2\ln 2+\ln 5}{\ln 2+\ln 5}\cdot \frac{\ln 5}{\ln 2+\ln 5}-e^{3\ln 3\cdot \frac{\ln 2}{\ln 3}}+\frac{2\ln 2}{\ln 3}\cdot \frac{2\ln 3}{\ln 2}&（第三步）\\ &=\left(\frac{\ln 2}{\ln 2+\ln 5}\right)^2+\frac{2\ln 2+\ln 5}{\ln 2+\ln 5}\cdot \frac{\ln 5}{\ln 2+\ln 5}-e^{3\ln 2}+\frac{2\ln 2}{\ln 3}\cdot \frac{2\ln 3}{\ln 2}&（第四步）\\ &=\left(\frac{\ln 2}{\ln 2+\ln 5}\right)^2+\frac{2\ln 2+\ln 5}{\ln 2+\ln 5}\cdot \frac{\ln 5}{\ln 2+\ln 5}-e^{\ln 8}+\frac{2\ln 2}{\ln 3}\cdot \frac{2\ln 3}{\ln 2}&（第四步）\\ &=\left(\frac{\ln 2}{\ln 2+\ln 5}\right)^2+\frac{2\ln 2+\ln 5}{\ln 2+\ln 5}\cdot \frac{\ln 5}{\ln 2+\ln 5}-8+\frac{2\ln 2}{\ln 3}\cdot \frac{2\ln 3}{\ln 2}&（第四步）\\ &=\frac{(\ln 2)^2+\ln 5(2\ln 2+\ln 5)}{(\ln 2+\ln 5)^2}-8+4&（第五步）\\ &=\frac{(\ln 2)^2+2\ln 2\cdot \ln 5+(\ln 5)^2}{(\ln 2)^2+2\ln 2\cdot \ln 5+(\ln 5)^2}-4&（第五步）\\ &=-3&（第五步）\\ \end{align*}

如果要用一些含对数的表达式表示另一个含对数的表达式，就： （1）按照前面化简含指数、对数的表达式的方法的第（1）（2）（3）（4）步转化所有表达式

。

（2）把每一个质数的对数值看作互不相关的变量，把已知条件看作有关对数值的方程，通过代入消元表示出要表示的代数式。

例2.（山东淄博实验中学2020期中）已知 $log127=m$ \log_{12} 7=m， $log123=n$ \log_{12} 3=n，试用含 $m$ m， $n$ n 且不含对数、指数的代数式表示 $log2863$ \log_{28} 63。

（1）按照前面化简含指数、对数的表达式的方法：

$m=log127=ln7ln12=ln7ln22\cdot3=ln72ln2+ln3n=log123=ln3ln12=ln3ln22\cdot3=ln32ln2+ln3log2863=ln63ln28=ln32\cdot7ln22\cdot7=2ln3+ln72ln2+ln7$ m=\log_{12} 7=\frac{\ln 7}{\ln 12}=\frac{\ln 7}{\ln 2^2\cdot 3}=\frac{\ln 7}{2\ln 2+\ln 3}\\ n=\log_{12} 3=\frac{\ln 3}{\ln 12}=\frac{\ln 3}{\ln 2^2\cdot 3}=\frac{\ln 3}{2\ln 2+\ln 3}\\ \log_{28} 63=\frac{\ln 63}{\ln 28}=\frac{\ln 3^2\cdot 7}{\ln 2^2\cdot 7}=\frac{2\ln 3+\ln 7}{2\ln 2+\ln 7}

（2）我们把 $ln2$ \ln 2， $ln3$ \ln 3， $ln7$ \ln 7 看作互不相关的变量，进行消元。首先利用第二个等式消去 $ln2$ \ln 2。可得 $ln2=(1-n)ln32n$ \ln 2=\frac{(1-n)\ln 3}{2n}。代入第一个等式，可得 $m=nln7ln3$ m=\frac{n\ln 7}{\ln 3}，于是 $ln7=mln3n$ \ln 7=\frac{m\ln 3}{n}。这样， $ln2$ \ln 2、 $ln7$ \ln 7 都用 $ln3$ \ln 3、 $m$ m、 $n$ n 表示了。我们再代入要表示的表达式：

$log2863=2ln3+ln72ln2+ln7=2ln3+mln3n2\cdot(1-n)ln32n+mln3n=m+2nm-n+1$ \log_{28} 63=\frac{2\ln 3+\ln 7}{2\ln 2+\ln 7}=\frac{2\ln 3+\frac{m\ln 3}{n}}{2\cdot \frac{(1-n)\ln 3}{2n}+\frac{m\ln 3}{n}}=\frac{m+2n}{m-n+1}

这就表示出来了。

有关指对幂函数图象的问题

若题目给出了一个指对幂函数（或指对幂函数的平移、对称，看见一个不是指对幂函数但很接近指对幂函数的函数解析式时，应该想一想这是不是指对幂函数的平移、对称）的图象，可以根据它的形态（即与坐标轴的交点，单调性，幂函数的凹凸性）得出有关参数的信息，或判断它不可能。若给出多个指对幂函数的图象，应依次处理。鉴别指对幂函数的图象，可以利用指对幂函数与坐标轴的交点：指数函数与 $x$ x 轴没有交点，与 $y$ y 轴正半轴有交点；对数函数与 $x$ x 轴正半轴有交点，与 $y$ y 轴没有交点；幂函数与坐标轴只相交于原点，或与坐标轴没有交点。

例1.（浙江学军中学2020期中）在同一直角坐标系下，函数 $y=1ax$ y=\frac{1}{a^x}， $y=loga(x+12)$ y=\log_a \left(x+\frac{1}{2}\right)（0"> $a>0$ a>0 且 $a\neq1$ a\neq 1）的图象可能是 A.

Image B.
Image C.
Image D.
Image

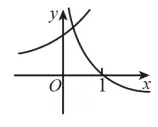
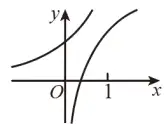
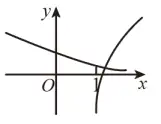
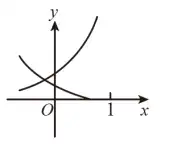
函数 $y=1ax$ y=\frac{1}{a^x} 就是指数函数 $y=(1a)x$ y=\left(\frac{1}{a}\right)^x。函数 $y=loga(x+12)$ y=\log_a \left(x+\frac{1}{2}\right) 不是对数函数，但它是对数函数 $y=logax$ y=\log_a x 向左平移 $12$ \frac{1}{2} 个单位长度。接下来我们看选项。

A选项，因为指数函数和 $x$ x 轴没有交点，所以和 $x$ x 轴有交点的一定是 $y=loga(x+12)$ y=\log_a \left(x+\frac{1}{2}\right)。考虑和 $x$ x 轴有交点的图象与 $x$ x 轴的交点。这个交点在 $(1,0)$ (1,0)，但由对数函数的性质，这个交点应该是 $(12,0)$ \left(\frac{1}{2},0\right)，故A选项错误。类似C选项错误。

B选项，与 $x$ x 轴有交点的是 $y=loga(x+12)$ y=\log_a \left(x+\frac{1}{2}\right)，它和 $x$ x 轴的交点位置符合条件，所以我们再看单调性。由单调性可知，这里 1"> $a>1$ a>1。然后我们看另一个函数图象，它是指数函数 $y=(1a)x$ y=\left(\frac{1}{a}\right)^x 的图象。这个图象与坐标轴的交点符合指数函数的性质，且单调递增，所以 1"> $1a>1$ \frac{1}{a}>1，但这与 1"> $a>1$ a>1 矛盾！所以B选项错误。

D选项，与 $x$ x 轴有交点的是 $y=loga(x+12)$ y=\log_a \left(x+\frac{1}{2}\right)，它和 $x$ x 轴的交点位置也符合条件，我们再看单调性。由单调性可知，这里 $0<a $1a>1$ \frac{1}{a}>1，符合 $0<a<span class=$ 0<a<1。所以D选项正确，本题选D。

例2.（浙江金华十校2020期末）在同一直角坐标系中，函数 $y=xa$ y=x^a， $y=log|a|(x-a)$ y=\log_{|a|}(x-a)（ $a\neq0$ a\neq 0）的图象不可能的是 A.

Image B.
Image C.
Image D.
Image

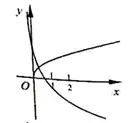
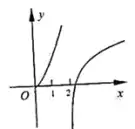
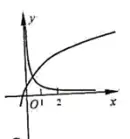
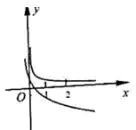
函数 $y=xa$ y=x^a 是幂函数，函数 $y=log|a|(x-a)$ y=\log_{|a|}(x-a) 是对数函数 $y=log|a|x$ y=\log_{|a|} x 向右平移 $a$ a 个单位长度。

A选项，因为幂函数要么过原点，要么和两坐标轴都没有交点，所以过原点的一定是幂函数 $y=xa$ y=x^a。根据它的单调性、凹凸性，可以得到 $0<a<span class=$ 0<a<1。再看另一个函数图象，它就是 $y=log|a|(x-a)$ y=\log_{|a|}(x-a) 的图象了。它与 $x$ x 轴的交点横坐标在 $0$ 0 和 $1$ 1 之间，但 $y=log|a|(x-a)$ y=\log_{|a|}(x-a) 与 $x$ x 轴的交点横坐标应为 $a+1$ a+1，不在 $0$ 0 和 $1$ 1 之间！所以A选项是不可能的。

B选项，和A选项同理，过原点的一定是幂函数 $y=xa$ y=x^a。根据它的单调性、凹凸性，可以得到 1"> $a>1$ a>1。再看另一个 $y=log|a|(x-a)$ y=\log_{|a|}(x-a) 的图象。它与 $x$ x 轴的交点横坐标大于 $2$ 2，而 $y=log|a|(x-a)$ y=\log_{|a|}(x-a) 与 $x$ x 轴的交点横坐标应为 $a+1$ a+1，确实大于 $2$ 2。单调性也符合。所以B选项是可能的。

C选项，两个图象都不过原点，这时和两坐标轴都没有交点的就是幂函数 $y=xa$ y=x^a 了。因为它和两坐标轴都没有交点，所以 $a $|a|>1$ |a|>1，于是单调性也符合。所以C选项是可能的。

D选项，和B选项同理，和两坐标轴都没有交点的就是幂函数 $y=xa$ y=x^a，于是 $a<span class=$ 0<|a|<1，所以单调性也符合。所以D选项是可能的，本题选A。

对于判断函数图象的问题，就按照图象过的定点，图象与 $y$ y 轴交点，函数值趋向无穷大的点（在解析式中常表现为分母为 $0$ 0 且分子不为 $0$ 0，或 $0$ 0 的对数乘以一个不趋向无穷的式子），图象的对称性，图象与 $x$ x 轴交点及函数在一定区间内的符号，函数的极值、极值点、单调性，函数值的大小的顺序从图象中提取信息，依次判断是否符合函数的解析式（本质上和我之前的文章”函数的概念与性质“中函数图象的判断的方法相同）。

例3.（湖北四校2022联考）若函数 $y=f(x)$ y=f(x) 的大致图象如图，则 $f(x)$ f(x) 的解析式可能为

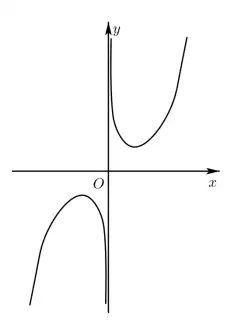
Image

A. $f(x)=x22x22x+1$ f(x)=\frac{x^22^x}{2^{2x}+1} B. $f(x)=22x+1x22x$ f(x)=\frac{2^{2x}+1}{x^22^x} C. $f(x)=x22x22x-1$ f(x)=\frac{x^22^x}{2^{2x}-1} D. $f(x)=22x-1x22x$ f(x)=\frac{2^{2x}-1}{x^22^x}

先看定点。但这个函数图象不过任何定点。

再看与 y 轴交点。这个函数图象和 y

轴没有交点。

再看函数值趋向无穷的点。这个函数图象在 x=0 时趋向无穷，所以我们看一看哪些选项也在 x=0 时趋向无穷。我们把 x=0 代入A选项，分子为 0，分母为 2，不趋向无穷，故A选项错误；代入B选项，分子为 2，分母为 0，函数值趋向无穷；代入C选项，分子为 0，分母为 0，没有足够信息判断；代入D选项，分子为 0，分母为 0

，也没有足够信息判断。

再看对称性。这个函数图象关于原点对称。我们把 x 变为 -x，B选项中得到 \frac{2^{-2x}+1}{(-x)^22^{-x}}=\frac{\frac{1}{2^{2x}}+1}{x^2\cdot \frac{1}{2^x}}=\frac{2^{2x}+1}{x^22^x}，和原来的函数值相等，所以B选项这个函数关于 y 轴对称，不关于原点对称，B选项错误；C选项中得到 \frac{(-x)^22^{-x}}{2^{-2x}-1}=\frac{x^2\cdot \frac{1}{2^x}}{\frac{1}{2^{2x}}-1}=\frac{x^22^x}{1-2^{2x}}

，和原来的函数值互为相反数，所以C选项这个函数确实关于原点对称；类似可以发现D选项这个函数也确实关于原点对称。

再看图象与 x 轴交点及其符号。这个函数图象与 x 轴没有交点，且在 0">x>0 时 0">f(x)>0。因为 0">x>0 时，0">x^2>0，0">2^x>0，1">2^{2x}>1

，所以C、D两选项都满足这个条件。

再看极值、极值点、单调性。这个函数图象在 0">x>0 时先单调递减，再单调递增。因为指数函数在 x 很大时会超过任何幂函数，所以C选项中，\frac{x^22^x}{2^{2x}-1}=\frac{x^2}{2^x-\frac{1}{2^x}} 在 x 很大时应该单调递减，趋近 0（因为它的分母增长比分子快得多），不可能单调递增，C选项错误。而D选项中，\frac{2^{2x}-1}{x^22^x}=\frac{2^x-\frac{1}{2^x}}{x^2} 在 x 很大时确实单调递增，因为它的分子增长比分母快得多。所以D选项正确，本题选D。

例4.（2019全国III卷）函数 y=\frac{2x^3}{2^x+2^{-x}} 在 [-6,6] 上的图象大致为 A.

Image B.
Image C.
Image D.
Image

先看定点。四个选项中，能确定函数图象过的定点都只有原点，从这一点判断不出什么来。

再看与 y

轴交点，这也判断不出什么来。

再看函数值趋向无穷大的点。四个图象都不存在这样的点。

再看对称性。ABD三个选项的图象都关于原点对称，C选项的图象关于 y 轴对称。我们把 x 换为 -x，容易发现函数值变为相反数，即 y=\frac{2x^3}{2^x+2^{-x}}

的图象关于原点对称，故C错误。

再看图象与 x 轴交点及其符号。0">x>0 时，AB两选项中都有 0">y>0，而D选项中 x>0 时 0">x^3>0，0">2^x>0，0">2^{-x}>0，所以 0">y=\frac{2x^3}{2^x+2^{-x}}>0，故D错误。（代入 x=1

或其它正值也可以发现这一点。）

再看极值、极值点、单调性，但AB两选项中，函数的极值、极值点、单调性都相同。

最后看函数值的大小。AB两选项的唯一差异在于 x=\pm 6 时，A中函数值很接近 0，而B中函数值更接近 \pm 8。所以我们就代入 x=6，得到此时 y=\frac{2x^3}{2^x+2^{-x}}=\frac{2\cdot 216}{64+\frac{1}{64}}\approx \frac{2\cdot 216}{64}=\frac{27}{4}=6.75，比较接近 8。所以A选项错误，B选项正确，本题选B。

指对幂函数单调性、奇偶性的应用

题目涉及复合函数的单调性时，可以利用指对幂函数的单调性来去掉一层函数，简化问题。除此以外，还要注意指对幂函数的定义域。

例1.（河北邢台2023六校联考）若函数 f(x)=\log_a (2x-ax^2) 在区间 \left(1,\frac{3}{2}\right] 上为减函数，则 a 的取值范围是__________。

我们利用对数函数的单调性，去掉外层的对数 \log_a。\log_a x 在 a>1 时单调递增，所以我们分类讨论：

（1）若 2x-ax^2>0 在 x\in \left(1,\frac{3}{2}\right] 时恒成立（为了使 f(x) 在 \left(1,\frac{3}{2}\right] 上有定义），且 2x-ax^2 在 \left(1,\frac{3}{2}\right] 上单调递增。恒大于 0 的条件可以用参变分离法处理：结合 x 的取值范围，原不等式可以变形为 a>0，所以 2x-ax^2 在 \left(1,\frac{3}{2}\right] 上单调递增就等价于 \frac{1}{a}\ge \frac{3}{2}，即 a\le \frac{2}{3}。综合以上的几个条件，此时 a 的取值范围为 \left(0,\frac{2}{3}\right]。

（2）若 1">a>1，那么 f(x)=\log_a (2x-ax^2) 在区间 \left(1,\frac{3}{2}\right] 上为减函数就等价于 0">2x-ax^2>0 在 x\in \left(1,\frac{3}{2}\right] 时恒成立，且 2x-ax^2 在 \left(1,\frac{3}{2}\right] 上单调递减。我们前面已经得到了恒成立的条件等价于 a>0）。综合以上的几个条件，此时 a 的取值范围为 \left(1,\frac{4}{3}\right)。

综上所述，a 的取值范围为 \left(0,\frac{2}{3}\right]\cup \left(1,\frac{4}{3}\right)。

若题目给出了一个函数 f(x)，然后要解形如 f(...)\_\_\_f(...) 或 f(...)\_\_\_a 的方程（不等式）（这里空白处填等号或不等号，下同），大多数情况下容易判断 f(x) 的单调性，且可能关于某个垂直于 x 轴的直线对称（一般为 y 轴）；若要解形如 f(...)+f(...)\_\_\_a 的方程（不等式），大多数情况下容易判断 f(x) 的单调性，且有一个纵坐标为 \frac{a}{2} 的对称中心（一般是点 \left(0,\frac{a}{2}\right)）。有了这条件一般就能去掉 f 了。如果不能立即去掉，分析不等式中各自变量的大小关系经常也是有用的。

例2.（湖北2022二模）已知函数 f(x)=\lg (|x|-1)+2^x+2^{-x}，则使不等式 x>0 的情况。此时 f(x)=\lg (x-1)+2^x+2^{-x}。显然 \lg (x-1) 在其定义域 (1,+\infty) 内单调递增，所以如果 2^x+2^{-x} 也单调递增就可以了。这可以用单调性的定义证明：若 x_2-x_1>0，所以 1">2^{x_2-x_1}>1，所以 0">2^{x_2-x_1}-1>0。又 1">2^{x_1}>1，2^x_1-2^{-x_2}>0。所以 0">(2^{x_2}+2^{-x_2})-(2^{x_1}+2^{-x_1})>0，这就证明了 2^x+2^{-x} 单调递增。也可以利用 2^x+2^{-x}=2^x+\frac{1}{2^x}，然后用对勾函数的单调性。于是 f(x) 在 (1,+\infty) 上单调递增。

这样就能去掉 f 了：|x+1|,|2x|>1（为了使 f(x+1),f(2x) 有定义）。分类讨论去绝对值，容易解得 x 的取值范围为 (-\infty,-2)\cup (1,+\infty)，本题选D。

例3.（河北“五个一联盟”2021一诊）已知函数 f(x)=\log_3 (x+\sqrt{x^2+1})-\frac{2}{3^x+1}，若 f(2a-1)+f(a^2-2)\le -2，则实数 a 的取值范围是 A. [-3,1] B. [-2,1] C. (0,1] D. [0,1]

这不等式是 f(...)+f(...)\_\_\_a 型，我们来判断 f(x) 的对称中心和单调性。由不等式知，f(x) 的对称中心应该是 (0,-1)，所以我们验证 f(x)+f(-x)=-2 就可以了：

\begin{align*} &f(x)+f(-x)\\ &=\log_3 (x+\sqrt{x^2+1})-\frac{2}{3^x+1}+\log_3 (-x+\sqrt{x^2+1})-\frac{2}{3^{-x}+1}\\ &=\log_3 ((x+\sqrt{x^2+1})(-x+\sqrt{x^2+1}))-\frac{2}{3^x+1}-\frac{2\cdot 3^x}{1+3^x}\\ &=\log_3 1-\frac{2(3^x+1)}{3^x+1}=-2 \end{align*}

所以 f(x) 确实有对称中心 (0,-1)。

显然 \log_3 (x+\sqrt{x^2+1})、-\frac{2}{3^x+1} 都在 (0,+\infty) 上单调递增，所以 f(x) 在 (0,+\infty) 上单调递增。由此就能去掉不等式 f(2a-1)+f(a^2-2)\le -2 中的 f：这个不等式等价于 (2a-1)+(a^2-2)\le 0，解得 a 的取值范围为 [-3,1]，本题选A。

例4.（上海交大附中2021期末）设 f(x)=|2^x-2|，a,b\in \mathbb{R}^+，且 a\neq b，则下列关系式中不可能成立的是 A. f(\sqrt{ab})>f\left(\frac{2ab}{a+b}\right)">f\left(\frac{a+b}{2}\right)>f(\sqrt{ab})>f\left(\frac{2ab}{a+b}\right) B. f\left(\frac{a+b}{2}\right)>f(\sqrt{ab})">f\left(\frac{2ab}{a+b}\right)>f\left(\frac{a+b}{2}\right)>f(\sqrt{ab}) C. f(\sqrt{ab})>f\left(\frac{a+b}{2}\right)">f\left(\frac{2ab}{a+b}\right)>f(\sqrt{ab})>f\left(\frac{a+b}{2}\right) D. f\left(\frac{2ab}{a+b}\right)>f\left(\frac{a+b}{2}\right)">f(\sqrt{ab})>f\left(\frac{2ab}{a+b}\right)>f\left(\frac{a+b}{2}\right)

这不等式是 f(...)\_\_\_f(...) 型，我们来判断 f(x) 的对称轴与单调性。显然 f(x) 没有对称轴；分类讨论去绝对值易得 f(x) 在 (-\infty,1) 上单调递减，在 (1,+\infty) 上单调递增。还是不好把 f 从不等式中去掉。但即使如此，我们分析不等式中每个自变量的大小关系也是有用的。我们接下来就比较 \frac{a+b}{2}、\sqrt{ab}、\frac{2ab}{a+b} 的大小。

由基本不等式，\frac{a+b}{2}\ge \sqrt{ab}。我们还想比较 \sqrt{ab} 和 \frac{2ab}{a+b} 的大小。同时除以 \sqrt{ab}，我们就想要比较 1 和 \frac{2\sqrt{ab}}{a+b} 的大小。而由基本不等式，a+b\ge 2\sqrt{ab}，即 \frac{2\sqrt{ab}}{a+b}\le 1，所以 \frac{2ab}{a+b}\le \sqrt{ab}。那么三个自变量的大小关系就是 \frac{2ab}{a+b}\le \sqrt{ab}\le \frac{a+b}{2}（其实这就是均值不等式的一部分）。

然后看选项。\frac{2ab}{a+b}、\sqrt{ab}、\frac{a+b}{2} 都在 f(x) 单调递增的一段时，A选项成立。\frac{2ab}{a+b}、\sqrt{ab}、\frac{a+b}{2} 都在 f(x) 单调递减的一段时，C选项成立。\sqrt{ab} 在 f(x) 图象 x=1 附近的低处，\frac{2ab}{a+b}、\frac{a+b}{2} 分别在两边的高处时，B选项成立。而可以发现，无论怎么样，f(\sqrt{ab}) 都不能成为三个函数值中最大的，所以D选项不可能成立，本题选D。如下图所示。

Image
若题目涉及最大值与最小值之和，或者交点坐标之和等可以利用对称性配对的量，可以考虑判断函数的对称性。应优先考虑 f(x) 关于 y 轴或 y 轴上一点对称。

例5.（广东中山实验中学2022期中）已知函数 f(x)=\frac{ax^2+a+\ln (\sqrt{x^2+1}+x)}{x^2+1}+\frac{4}{a}，若 f(x) 最大值为 M，最小值为 N，a\in [1,3]，则 M+N 的取值范围是__________。

因为有对称中心的函数图象中，最大值和最小值可以利用对称性配对，所以我们考虑判断 f(x) 的对称性。我们需要中心对称，所以我们优先考虑 f(x) 关于 y 轴上一点对称，也就是判断 f(x)+f(-x) 是否为定值。我们有

\begin{align*} &f(x)+f(-x)\\ &=\frac{ax^2+a+\ln (\sqrt{x^2+1}+x)}{x^2+1}+\frac{4}{a}+\frac{ax^2+a+\ln (\sqrt{x^2+1}-x)}{x^2+1}+\frac{4}{a}\\ &=\frac{2ax^2+2a+\ln (\sqrt{x^2+1}+x)+\ln (\sqrt{x^2+1}-x)}{x^2+1}+\frac{8}{a}\\ &=\frac{2a(x^2+1)+\ln ((\sqrt{x^2+1}+x)(\sqrt{x^2+1}-x))}{x^2+1}+\frac{8}{a}\\ &=2a+\frac{8}{a}+\frac{\ln 1}{x^2+1}=2a+\frac{8}{a} \end{align*}

为定值，所以 f(x) 确实有对称中心 \left(0,a+\frac{4}{a}\right)。那么由对称性，M+N=2a+\frac{8}{a}。又 a\in [1,3]，结合对勾函数的单调性知，M+N 的取值范围为 [8,10]。

这里严格来说还要说明 M、N 确实存在。因为 f(x)=\frac{ax^2+a+\ln (\sqrt{x^2+1}+x)}{x^2+1}+\frac{4}{a}=a+\frac{4}{a}+\frac{\ln (\sqrt{x^2+1}+x)}{x^2+1}，所以我们说明 g(x)=\frac{\ln (\sqrt{x^2+1}+x)}{x^2+1} 有最大、最小值就可以了。我们发现，x 很大时，x+\sqrt{x^2+1} 增长的速度约等于 2x，那么 \ln (\sqrt{x^2+1}+x) 增长的速度就约等于 \ln x，而 \ln x 增长的速度远小于分母上的 x^2+1，所以 x 很大时 g(x)=\frac{\ln (\sqrt{x^2+1}+x)}{x^2+1} 要接近 0。而易知 0">x>0 时 0">g(x)>0，且 g(0)=0，所以可以作出 g(x) 在 0">x>0 时的图象大致如下图所示：

Image
由对称性，g(x) 的图象大致如下图所示：

Image
所以 g(x) 确实有最大、最小值。这就说明了 M、N 存在。不过这不是一个严格的证明，严格证明 M、N 存在需要用导数。

有关指对幂函数的比大小问题

现阶段，有关指对幂函数的比大小问题主要有下面几种方法。 （1）通过计算估计需要比较的数的值。比较一个数和 0、1 的大小经常很有用，而且也很方便，所以看见比大小问题应该先考虑和 0、1 比较。估计指数的值时，有近似公式 e^x\approx 1+x+\frac{x^2}{2}，它在 b>1，a>0>b B. b>0">a>b>0 C. a>0">b>a>0 D. 0>a">b>0>a

由已知条件 m=\log_9 10。我们先比较 a 和 0 的大小，这也就是要比较 10^{\log_9 10} 和 11 的大小。这里有一个指数，我们按照方法（2），取一个对数，所以我们只需要比较 \log_9 10 和 \log_{10} 11 的大小。接下来，按照方法（3）求值就行了：\log_9 10=\frac{\ln 10}{\ln 9}=\frac{\ln 2+\ln 5}{2\ln 3}\approx \frac{0.693+1.609}{2\cdot 1.099}=\frac{2.302}{2.198}，\log_{10} 11=\frac{\ln 11}{\ln 10}\approx \frac{2.398}{2.302}，所以 \log_{10} 11">\log_9 10>\log_{10} 11，所以 11">10^{\log_9 10}>11，所以 0">a>0。

类似，我们比较 b 和 0 的大小，也就是要比较 8^{\log_9 10} 和 9 的大小。取一个对数，我们只需要比较 \log_9 10 和 \log_8 9 的大小。再按照方法（3）求值：已经求出了 \log_9 10\approx \frac{2.302}{2.198}，又 \log_{8} 9=\frac{\ln 9}{\ln 8}=\frac{2\ln 3}{3\ln 2}\approx \frac{2\cdot 1.099}{3\cdot 0.693}=\frac{2.198}{2.079}，所以 x>2 时，\log_x (x+1)">\log_{x-1}x>\log_x (x+1)。这也就是要证明 \frac{\ln (x+1)}{\ln x}">\frac{\ln x}{\ln (x-1)}>\frac{\ln (x+1)}{\ln x}，即 \ln (x-1)\cdot \ln (x+1)">(\ln x)^2>\ln (x-1)\cdot \ln (x+1)。这看起来像平方差公式，要是能把右边的乘积变成和就好了，这样对数里面就是平方差了。于是，由基本不等式的变形，有 k>0）与对数函数 y=\log_a x（1">a>1）的图象相交于 A、B 两点，经过 A 点的线段 CD 垂直于 y 轴，垂足为 C。若四边形 OCBD 为平行四边形，且 S_{四边形OCBD}=4，则实数 k、a 的值分别为 A. k=1,a=2 B. k=\frac{1}{2},a=2 C. k=2,a=2 D. k=1,a=4

先把图画出来：

Image

四边形 OCBD 为平行四边形就等价于 A 是 OB 的中点，也是 CD 的中点。适当地取点 D 总能使得 A 是 CD 的中点，所以关键就是 A 是 OB 的中点。我们设 A 的横坐标为 x_A，由 A 为交点得 kx_A=\log_a x_A。设 B 的横坐标为 x_B，由 B 为交点得 kx_B=\log_a x_B。由 A 为 OB 中点得 x_B=2x_A。代入可得 2kx_A=\log_a (2x_A)。

化简一下两个等式，得到 kx_A=\frac{\ln x_A}{\ln a}，2kx_A=\frac{\ln x_A+\ln 2}{\ln a}。注意到 x_A 经常在对数中出现，我们换元 t=\ln x_A。那么 x_A=e^t，所以 ke^t=\frac{t}{\ln a}，2ke^t=\frac{t+\ln 2}{\ln a}。两式相除得 2=\frac{t+\ln 2}{t}，解得 t=\ln 2，所以 x_A=e^t=2。（也可以不换元，直接解 \ln x_A。）

我们还有四边形面积为 4 的条件没用。容易发现这等价于 2x_A\cdot kx_A=4。由此容易解得 k=\frac{1}{2}。把 x_A=2、k=\frac{1}{2} 代入到 kx_A=\frac{\ln x_A}{\ln a} 中得 1=\frac{\ln 2}{\ln a}，即 \ln a=\ln 2。由此可以直接解出 a=2。故本题选B。

例4.（江苏淮阴中学2022月考）设 f(x) 是定义在 \mathbb{R} 上的偶函数，且当 x\le 0 时，f(x)=2^{-x}。若对任意的 x\in [m,m+1]，不等式 f(x)\ge f^2(x-m) 恒成立，则正数 m 的取值范围为 A. [1,+\infty) B. (1,+\infty) C. (0,1) D. $(0,1] $

易知 x\ge 0 时 f(x)=2^x。那么，因为 0">m>0，m">x>m，所以 0">x>0，0">x-m>0，所以我们的不等式就可以转化为 2^x\ge (2^{x-m})^2 恒成立。

注意到 x 经常在指数上出现，所以我们换元 t=2^x。那么 t 的取值范围为 [2^m,2^{m+1}]。然后我们想要把我们的不等式用 t 表示。这很容易，因为 2^{x-m}=\frac{2^x}{2^m}=\frac{t}{2^m}，所以我们的不等式能转化为 t\ge \left(\frac{t}{2^m}\right)^2 恒成立。结合 0">t>0，我们把它参变分离，转化为 2^{2m}\ge t。想让它恒成立，t 只需取最大值 2^{m+1}，所以只需要 2^{2m}\ge 2^{m+1}，也就是 2m\ge m+1，解得 m 的取值范围为 [1,+\infty)。故本题选A。

例5.（辽宁大连2019期末）已知 \alpha 和 \beta 分别是函数 f(x)=2^x+x-5 与 g(x)=\log_8 x^3+x-5 的零点，则 2^\alpha+\log_2 \beta 的值为 A. 4+\log_2 3 B. 2+\log_2 3 C. 4 D. 5

这式子既含对数，也含指数，我们考虑用同构。先把 g(x) 化简一下。容易发现它等于 \log_2 x+x-5。那么同构就比较明显了：f(x) 的表达式中把 x 换为 \log_2 x 就得到 g(x)，即 g(x)=f(\log_2 x)。于是 f(\alpha)=f(\log_2 \beta)=0。而显然 f(x) 单调递增，所以我们去掉 f，得到关系式 \alpha=\log_2 \beta。那么 2^\alpha+\log_2 \beta=\beta+\log_2 \beta，而我们的已知条件就是 \log_2 \beta+\beta-5=0，所以 2^\alpha+\log_2 \beta=5。

例6.（湖北襄阳五中2023开学考）已知实数 \alpha，\beta 满足 \alpha e^{\alpha-3}=1，\beta (\ln \beta -1)=e^4，则 \alpha \beta 的值为 A. e^3 B. 2e^3 C. 2e^4 D. e^4

这式子既含对数，也含指数，我们考虑用同构。\alpha e^{\alpha-3}=1 就等价于 \alpha e^\alpha=e^3。这是 xe^x 的形式，所以我们试图把另一个等式也变形为 xe^x 的形式，或者 x\ln x 的形式（因为把 xe^x 中的 x 换为 \ln x 就得到 x\ln x）。这是可以做到的：\beta (\ln \beta-1)=e^4 等价于 \beta \ln \frac{\beta}{e}=e^4，也就等价于 \frac{\beta}{e}\ln \frac{\beta}{e}=e^3。现在，我们就发现 \alpha e^\alpha=\frac{\beta}{e}\ln \frac{\beta}{e}=\ln \frac{\beta}{e}\cdot e^{\ln \frac{\beta}{e}}，两边都是 xe^x 的形式。而因为 f(x)=xe^x 在 (0,+\infty) 上单调递增，且显然 \alpha、0">\ln \frac{\beta}{e}>0，所以 \alpha=\ln \frac{\beta}{e}。这样，我们要求的 \alpha \beta=\beta \ln \frac{\beta}{e}，而我们知道这等于 e^4，故本题选D。

对于复合函数的零点问题，应该先考虑内层函数等于定值时 x 在一定范围内的解及其个数，再考虑外层函数的零点个数及分布。

例7.（吉林梅河口五中2022期末）已知 f(x)=2^x，g(x)=\log_2 x。是否存在实数 b 使得对任意 m\in [0,1]，关于 x 的方程 4g^2(x)-4b|g(x)|+3b-1-f(m)=0 在区间 \left[\frac{1}{8},4\right] 上总恰有三个不等根 x_1，x_2，x_3？若存在，求出实数 b 及 x_1x_2x_3 的取值范围；若不存在，请说明理由。

容易看出这是一个复合函数的零点问题：设 h(x)=4x^2-4bx+3b-1-2^m，那么我们的条件就是 h(|g(x)|) 在 \left[\frac{1}{8},4\right] 上有三个零点。先考虑内层函数 |g(x)|=|\log_2 x| 为定值时，x 在 \left[\frac{1}{8},4\right] 上的解及其个数。零点问题可以画出函数图象辅助思考：

Image

由图，设 |\log_2 x|=c（c 为定值），那么 h(0)=3b-1-2^m>0，h(2)=15-5b-2^m\le 0，h(3)=35-9b-2^m\ge 0。其实 h(2)=0 时还需要对称轴 2">\frac{b}{2}>2，这我们之后验算一下就行。

Image

这又是恒成立问题，我们参变分离：2^m">3b-1>2^m，15-5b\le 2^m，35-9b\ge 2^m。结合 m\in [0,1]，我们只需 2">3b-1>2，15-5b\le 1，35-9b\ge 2，解得 \frac{14}{5}\le b\le \frac{11}{3}。不过这不满足 2">\frac{b}{2}>2，所以其实 h(2) 不能等于 0，重新解一下，得到 b 的取值范围为 \left(\frac{14}{5},\frac{11}{3}\right]。

还要求 x_1x_2x_3 的范围。由我们之前的讨论，\{x_1,x_2,x_3\}=\{2^{x_a},2^{-x_a},2^{-x_b}\}，所以 x_1x_2x_3=2^{-x_b}。而 x_b 的取值范围是 (2,3]，所以 x_1x_2x_3 的取值范围就是 \left[\frac{1}{8},\frac{1}{4}\right)。

指对幂函数的实际应用

对于指对幂函数的实际应用问题，通过待定系数法确定参数，或者通过解方程求出要求的量就可以了。

例1.（2020新高考I卷）基本再生数 R_0 与世代间隔 T 是新冠肺炎的流行病学基本参数。基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间。在新冠肺炎疫情初始阶段，可以用指数模型：I(t)=e^{rt} 描述累计感染病例数 I(t) 随时间 t（单位：天）的变化规律，指数增长率 r 与 R_0，T 近似满足 R_0=1+rT。有学者基于已有数据估计出 R_0=3.28，T=6。据此，在新冠肺炎疫情初始阶段，累计感染病例数增加 1 倍需要的时间约为（\ln 2\approx 0.69） A. 1.2 天 B. 1.8 天 C. 2.5 天 D. 3.5 天

题目中实际有用的信息只有 I(t)=e^{rt}，R_0=1+rT，R_0=3.28，T=6。首先我们可以求出 r 来。因为 R_0=1+rT，所以 r=\frac{R_0-1}{T}=\frac{3.28-1}{6}=0.38。所以 I(t)=e^{0.38t}。所以我们就要求 e^{0.38t} 增加一倍需要的时间。

设 e^{0.38t} 增加一倍需要的时间为 t_1。那么，从时刻 t 开始，到时刻 t+t_1，I(t) 就应该变为原来的两倍，即 \frac{I(t+t_1)}{I(t)}=2。又 \frac{I(t+t_1)}{I(t)}=\frac{e^{0.38(t+t_1)}}{e^{0.38t}}=e^{0.38t_1}，所以 e^{0.38t_1}=2，所以 0.38t_1=\ln 2，所以 t_1=\frac{\ln 2}{0.38}\approx \frac{0.69}{0.38}\approx 1.8。故本题选B。

例2.（北京通州2021一模）著名数学家、物理学家牛顿曾提出：物体在空气中冷却，如果物体的初始温度为 \theta_1^\circ \text{C}，空气温度为 \theta_0^\circ \text{C}，则 t\text{min} 后物体的温度 \theta（单位：{}^\circ \text{C}）满足：\theta=\theta_0+(\theta_1-\theta_0)e^{-kt}（其中 k 为常数，e=2.71828...）。现有某物体放在 20^\circ \text{C} 的空气中冷却，2\text{min} 后测得物体的温度为 52^\circ \text{C}，再经过 6\text{min} 后物体的温度冷却到 24^\circ \text{C}，则该物体初始温度是 A. 80^\circ \text{C} B. 82^\circ \text{C} C. 84^\circ \text{C} D. 86^\circ \text{C}

题目给出了 \theta_0=20（为了方便，单位省略）。我们用待定系数法解出两个未知参数 k、\theta_1。已知条件相当于是说 t=2 时 \theta=52，t=2+6=8 时 \theta=24。代入函数解析式，得

\begin{align*} 52&=20+(\theta_1-20)e^{-2k}\\ 24&=20+(\theta_1-20)e^{-8k} \end{align*}

对于这个方程，因为 k 经常出现在指数上，我们按照上一节的方法，换元 m=e^{-2k}，代入并化简得

\begin{align*} 32&=(\theta_1-20)m\\ 4&=(\theta_1-20)m^4 \end{align*}

相除消去 \theta_1 得 m^3=\frac{1}{8}，所以 m=\frac{1}{2}。代入原方程易得 \theta_1=84，即初始温度为 84^\circ \text{C}，故本题选C。

本文使用 Zhihu On VSCode 创作并发布

以上就是关于《高中数学：指数函数、对数函数、幂函数-指数函数幂函数对数函数增长的比较》的全部内容，本文网址：https://www.7ca.cn/baike/64010.shtml，如对您有帮助可以分享给好友，谢谢。

标签:

声明