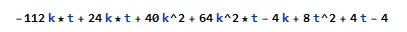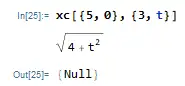写在前面
很多时候,在算解析几何题的时候,都会偷懒(划去)使用mathematica来化简,尤其是在展示自己的硬算技巧时。但是每次都得连立方程,显得颇为麻烦,故将解析几何里一些常用函数写在这里。如果您已经熟识mathematica,可以直接跳到最后“这里是全部的代码”获取全部代码;如果您尚未使用过mathematica,可以先看一下第一部分的mathematica简介(极简的教程)。每个函数对应的介绍都在各个函数的章节给出,文章的左边有目录,点击可以跳转到对应的部分。本文不定期更新
这文章现在21赞57收藏,赞收比将近1:3……码字不易,望您能点个赞
Tommy 祖:Mathematica-解析几何器 2.03 赞同 · 13 评论文章
Mathematica极简入门教程
1、获得一个mathematica
mathematica是一款付费的数学软件,官网在这里
Wolfram Mathematica: 現代技術計算www.wolfram.com/mathematica/
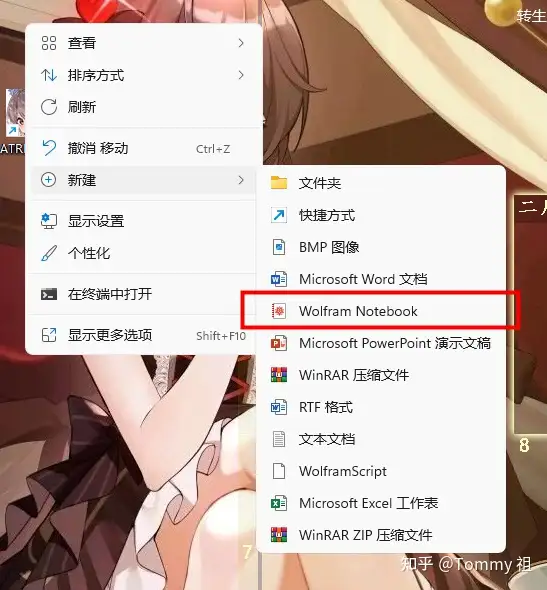
2、新建一个mathematica notebook
如图,在安装mathematica后,新建栏会有新建wolfram notebook
3、输入
一切的运算用你所熟知的符号就好。比如,假如要计算 3+11−485×8\frac{3+11-48}{5\times8} ,可以这样输入
然后呢,得出结果需要按shift+enter,单独按enter是换行
注意,/只对后面的一个字母/数字起作用,如果相对后面的整体进行除的运算,需要像上面那样用括号括起来。^等同理
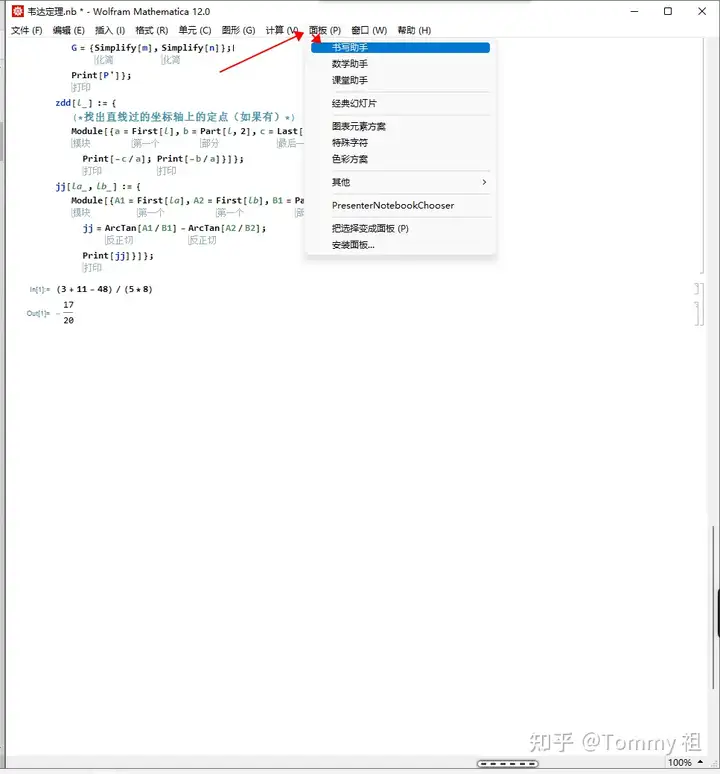
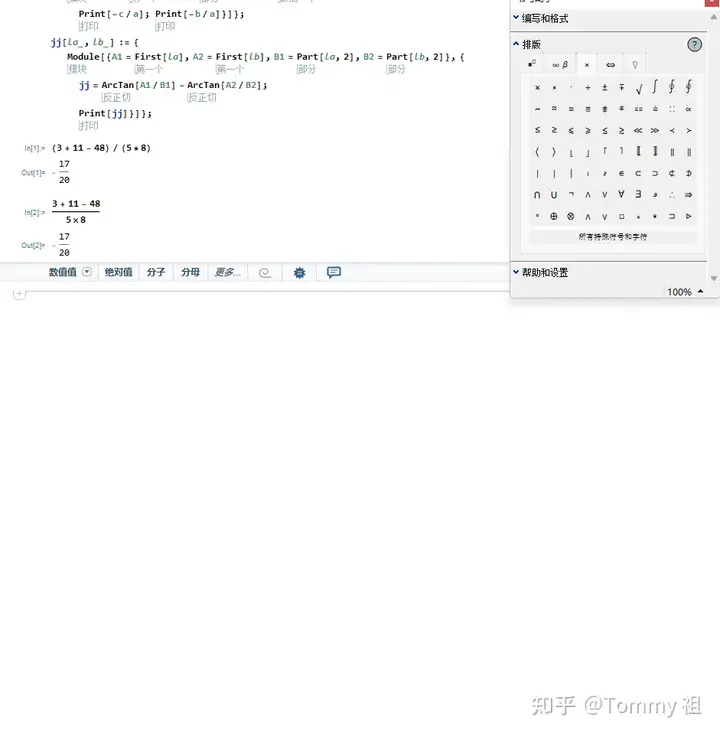
也可以点击上方的“面板”,“书写助手”,会出现输入公式格式的按钮以及快捷键
得出的是一样的结果
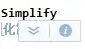
在输入函数时,把鼠标放到函数上会出现这样一个小框,
左边的可以看到该函数的输入格式和功能,右边的可以打开对应的mathematica文档进行内容的详细的查看
输入函数时要用[ ]把后面的内容括起来
4、在做解析几何时可能用到的函数
首先是Simplify ,可以化简一个含参的表达式。比如,化简
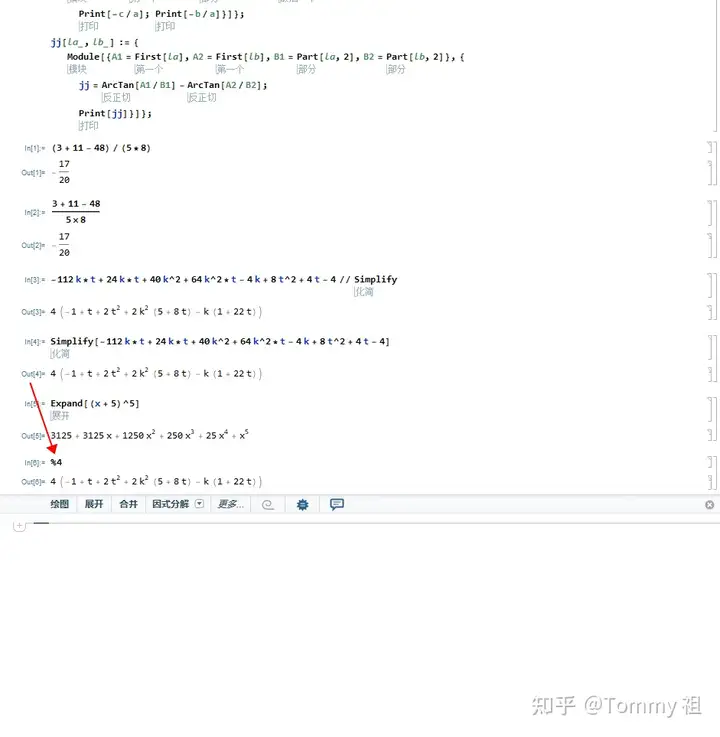
可以在他的后面打上//Simplify,就像这样
(注意这里我想写 ktkt 的时候用了k*t,这是因为如果是连着的字母会被mathematica判定为一个叫做“kt”的变量,与k和t无关,毕竟他好歹算个编程软件 )
也可以把它放到一个Simplify[ ]函数里,像这样
有些时候,一次单纯的Simplify不能将一个非常复杂的式子化到最简,可以使用FullSimplify函数
然后是Expand函数,这个函数就是将一个式子展开
调用某一次的输出结果,用% +对应次数来进行。比如,我想调用Out[4]的结果,就可以直接输入%4 来进行
限于文章篇幅,这里给出一些其他的常用函数,就不赘述了
Solve解方程,
Factor因式分解
Sin Cos Tan ArcSin等三角函数
Sqrt开根号
……
在做许多道题时,可能会用到
Clear["Global`*"]
表示清除所有的变量,你可不想把上一题的交点坐标用到下一题里。注意,Global后面是`,英文输入法下的键盘Tab上面的那个键(画着~的那个,底下那个点)
Clear[bainliang]
表示单独清除“bianliang”这个变量。当然,“bianliang”这个名字可以是其他的,表示清除该变量
各个函数和简介
椭圆、双曲线的韦达定理wd1
输入:
wd1[{a,b},{A,B,C},1/0,1/0]
求得的是直线 Ax+By+C=0Ax+By+C=0 与二次曲线 x2a2+y2b2=1\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 联立后的韦达定理,当b是实数时表示椭圆,b是虚数时表示双曲线。
可用全局变量:
两交点坐标P,Q,以及各自的横纵坐标x1,x2,y1,y2,
例子:求 ()y=kx+1(whichiskx−y+1=0),x24+x23=1y=kx+1(which\space is\space kx-y+1=0),\frac{x^2}{4}+\frac{x^2}3=1 联立的韦达定理,不展开,输出点的坐标
会输出一个null,这是因为自定义函数里直接把输出Print出来了,不用管他就好
代码:
wd1[m_,n_,i_,j_]:={(*椭圆韦达定理*)a=Part[m,1];b=Part[m,2];A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];P={x1,y1};Q={x2,y2};If[j==1,{Print["P ",P];Print["Q ",Q]}];If[i==1,{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1+x2]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1*x2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1+y2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1*y2]]},{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1+x2]]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1*x2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1+y2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1*y2]]]}]};
抛物线韦达定理wd2
输入:
wd2[p,{A,B,C},1/0,1/0]
求的是 y2=2px,Ax+By+C=0y^2=2px,Ax+By+C=0 联立的韦达定理
这里有一个缺点就是默认方程是 y2=2pxy^2=2px ,如果是 x2=2pyx^2=2py 的话只能手动把x与y翻转一下了
1,0的含义同wd1
可用全局变量:
两交点坐标P2,Q2,
各自的横纵坐标x1,x2,y1,y2
要注意的是,因为一般不会同时出现两个圆锥曲线,因此笔者并没有将抛物线与椭圆的交点所用的变量名分开(都是P,Q),如果在实际题目中遇到了,则相应的变量会变成最后一次输出的值——如果题目中恰好出现了两个圆锥曲线,可以手动在代码中改一下变量名——第四行到第七行的开头改了就好
例子:求 y=kx+1,y2=4xy=kx+1,y^2=4x 的联立韦达定理
代码:
wd2[p_,n_,i_,j_]:={(*抛物线韦达定理*)A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];P2={x1,y1};Q2={x2,y2};If[j==1,{Print["P ",P2];Print["Q ",Q2]}];If[i==1,{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1+x2]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1*x2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1+y2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1*y2]]},{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1+x2]]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1*x2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1+y2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1*y2]]]}]};
任意两点间的距离xc
xc这里是“弦长”的简写
输入:
xc[{x1,y1},{x2,y2}]
这个真的……没什么好说的,表示(x1,y1)到(x2,y2)的距离
可用全局变量:
这两点间的距离s
例子:
(1)求(5,0)到(3,t)的距离
(2)求上一个例子里,点P与原点的距离
由于这里点P的坐标是全局变量,可用直接使用(注意P要大写)
代码(巨简单):
xc[A1_,A2_]:={(*任意两点间的长度*)s=Simplify[Sqrt[(First[A1]-First[A2])^2+(Last[A2]-Last[A1])^2]];Print[s]};
直线截椭圆得到的弦长xc1
输入:
xc1[{a,b},{A,B,C},1/0]
上面各字母的意义与韦达定理相同,没有了第四个输入是因为不用控制是否输出点的坐标了
可用全局变量:
xc,即求的这个弦长
例子:
求wd1中例子里截得的弦长
注意这个式子可能是负值,因为没有加绝对值
代码:
xc1[m_, n_, i_] := {
(*直线截椭圆得到的弦长*)
a = Part[m, 1]; b = Part[m, 2];
A = Part[n, 1]; B = Part[n, 2]; c = Part[n, 3];
x1 = x /.
First[Solve[{x^2/a^2 + y^2/b^2 == 1, A*x + B*y + c == 0}, {x,
y}]];
x2 = x /.
Last[Solve[{x^2/a^2 + y^2/b^2 == 1, A*x + B*y + c == 0}, {x, y}]];
y1 = y /.
First[Solve[{x^2/a^2 + y^2/b^2 == 1, A*x + B*y + c == 0}, {x,
y}]];
y2 = y /.
Last[Solve[{x^2/a^2 + y^2/b^2 == 1, A*x + B*y + c == 0}, {x, y}]];
xc = Simplify[(x1 - x2)*Sqrt[1 + A^2/B^2]];
If[i == 1, Print[xc], Print[Expand[xc]]]};
直线截抛物线所得的弦长xc2
方法与前面基本相同,在此不再赘述
xc2[p_,n_,i_]:={(*直线截抛物线得到的弦长*)A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];xc=Simplify[(x1-x2)Sqrt[1+A^2/B^2]];If[i==1,Print[xc],Print[Expand[xc]]]};
过任意两点的直线方程/系数
输入:
zx[{x1,y1},{x2,y2},1/0]
1表示输出直线方程,0表示输出直线的系数
可用全局变量:
fc直线方程,这个可以抄下来,但在mathematica上没什么用
xs直线系数{A,B,C},可以输入到其他函数中
例子:
求 (k^2+1,0),(4,3t-1) 所连成的直线
这里分别展示了一下方程和系数分别是什么样子的输出形式
代码:
zx[A1_,A2_,i_]:={(*过任意两点的直线方程/系数*)Module[{a=A1,b=A2},{w1=AppendTo[a,1];w2=AppendTo[b,1];fc=Det[{w1,w2,{x,y,1}}];a1=First[a];b1=Last[a];a2=First[b];b2=Last[b];xs={Simplify[a1-b2],Simplify[a2-a1],Simplify[a1*b2-a2*b1]};If[i==1,Print[fc],Print[xs]]}]};
两个直线的交点jd
输入:
jd[{A,B,C},{A,B,C}]
表示求直线 Ax+By+C=0,Ax+By+C=0 的交点
可用全局变量:
G,交点坐标
m,交点横坐标;n,交点纵坐标
例子:
求 y=kx+1,x=ky+1 的交点坐标
代码:
jd[l1_,l2_]:={(*两个直线的交点*)m=x/.First[Solve[{First[l1]*x+Part[l1,2]*y+Last[l1]==0,First[l2]*x+Part[l2,2]*y+Last[l2]==0},{x,y}]];n=y/.Last[Solve[{First[l1]*x+Part[l1,2]*y+Last[l1]==0,First[l2]*x+Part[l2,2]*y+Last[l2]==0},{x,y}]];G={Simplify[m],Simplify[n]};Print[P]};
任意三点围成的面积mj
输入:
mj[{x1,y1},{x2,y2},{x3,y3}]
表示这三个点围成的三角形的面积(可能是负值)
可用全局变量
mj求出的面积
例子
求wd1中P、Q和椭圆右焦点F围成的三角形面积
代码
jd[l1_,l2_]:={(*两个直线的交点*)m=x/.First[Solve[{First[l1]*x+Part[l1,2]*y+Last[l1]==0,First[l2]*x+Part[l2,2]*y+Last[l2]==0},{x,y}]];n=y/.Last[Solve[{First[l1]*x+Part[l1,2]*y+Last[l1]==0,First[l2]*x+Part[l2,2]*y+Last[l2]==0},{x,y}]];G={Simplify[m],Simplify[n]};Print[P]};
过坐标轴上的点zdd
这是“轴定点”的缩写
输入
zdd[{A,B,C}]
可用全局变量:无
例子:懒得给了,就是求一个直线的横截距和纵截距
代码:还是巨简单
zdd[l_]:={(*找出直线过的坐标轴上的定点(如果有)*)Module[{a=First[l],b=Part[l,2],c=Last[l]},{Print[-c/a];Print[-b/a]}]};
两直线的夹角jj
输入
jj[{A1,B1,C1},{A2,B2,C2}]
可用全局变量
jj两直线的夹角
例子
求y=2x和y=3x的夹角的余弦值
由于是余弦值需要另外算一下余弦
使用RootApproximation函数可以把解析值算出来
代码
jj[la_,lb_]:={Module[{A1=First[la],A2=First[lb],B1=Part[la,2],B2=Part[lb,2]},{jj=ArcTan[A1/B1]-ArcTan[A2/B2];Print[jj]}]};
过两点直线的斜率xl
输入
xl[{x1,y1},{x2,y2}]
可用全局变量
xl表示该直线的斜率
例子
下面的“一道例题”有用到
代码
xl[A_, B_] := {
(*给出过两点直线的斜率*)
Module[{x1 = First[A], x2 = First[B], y1 = Part[A, 2],
y2 = Part[B, 2]}, {
xl = Simplify[(y1 - y2)/(x1 - x2)]}]};
一道例题
这是笔者的一道作业题,以及笔者打的草稿。很显然,笔者算错了(解析式是对的),下面就来用解析几何器来检查一下我的错误
得出答案
首先,这是一个抛物线,说明我们应该用韦达2来得到M和N的坐标
然后呢,我们想得到TM TN的斜率,这里我们使用xl函数,然后再把它们相加,这里就一口气给出了
注意,最上面有一个Clear["xl"]表示清除掉xl变量(不加引号写成Clear[xl]也可以)。为啥呢?因为函数前后是不变的,也就是说,如果我们不把斜率xl这个变量清除掉, 那么算出来的k1会被带到k2的运算中。
然后,令这个式子等于 -\frac83 ,这里我们用Reduce函数来化简方程
注意方程用==
好了,我们现在得到了等式 k=t+1 ,再得出过的定点就易如反掌了。但问题是,这样仅仅是给出了答案,笔者的草稿错在哪里了呢?这就需要下一部分:找出错误
找出错误
先clear一下global,不要韦达。这是因为,我们要首先对我算的式子进行化简,也就说,式子里是要带着x1,y1这些数的。如果韦达了,那么mathematica化简的时候就会把坐标带入,无法得到想要的表达式
我们想要的斜率的表达是 \frac{y_1+2}{x_1-\frac12}+\frac{y_2+2}{x_2-\frac12}\\ 那么我们把这个式子输入到mathematica里,然后化简
诶他不出结果!没办法,mathematica认为这就是最简的形式了。那我们只好再分别把分子和分母输入进去
按alt+7可以进行纯文本输入
和笔者写的对比一下,一样。然后再把直线方程 x=ky+t 带入
再和笔者的草稿对比一下,发现了!我在展开的时候, k^2y_1y_2 变成了 ky_1y_2
(怎么样,这样检查是不是比自己一点一点重推一遍方便多了)
剩下的步骤就和上面一样了,带入方程然后reduce,然后因式分解,最后得出的答案和上面一样
这里是全部的代码放在一起,方便复制
wd1[m_,n_,i_,j_]:={(*椭圆韦达定理*)a=Part[m,1];b=Part[m,2];A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];P={x1,y1};Q={x2,y2};If[j==1,{Print["P ",P];Print["Q ",Q]}];If[i==1,{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1+x2]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1*x2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1+y2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1*y2]]},{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1+x2]]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1*x2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1+y2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1*y2]]]}]};wd2[p_,n_,i_,j_]:={(*抛物线韦达定理*)A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];P2={x1,y1};Q2={x2,y2};If[j==1,{Print["P ",P2];Print["Q ",Q2]}];If[i==1,{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1+x2]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Simplify[x1*x2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1+y2]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Simplify[y1*y2]]},{Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)+\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1+x2]]];Print["\!\(\*SubscriptBox[\(x\),\(1\)]\)\!\(\*SubscriptBox[\(x\),\\(2\)]\)=",Expand[Simplify[x1*x2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)+\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1+y2]]];Print["\!\(\*SubscriptBox[\(y\),\(1\)]\)\!\(\*SubscriptBox[\(y\),\\(2\)]\)=",Expand[Simplify[y1*y2]]]}]};xc[A1_,A2_]:={(*任意两点间的长度*)s=Simplify[Sqrt[(First[A1]-First[A2])^2+(Last[A2]-Last[A1])^2]];Print[s]};xc1[m_,n_,i_]:={(*直线截椭圆得到的弦长*)a=Part[m,1];b=Part[m,2];A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{x^2/a^2+y^2/b^2==1,A*x+B*y+c==0},{x,y}]];xc=Simplify[(x1-x2)*Sqrt[1+A^2/B^2]];If[i==1,Print[xc],Print[Expand[xc]]]};xc2[p_,n_,i_]:={(*直线截抛物线得到的弦长*)A=Part[n,1];B=Part[n,2];c=Part[n,3];x1=x/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];x2=x/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y1=y/.First[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];y2=y/.Last[Solve[{y^2==2p*x,A*x+B*y+c==0},{x,y}]];xc=Simplify[Abs[x1-x2]Sqrt[1+A^2/B^2]];If[i==1,Print[xc],Print[Expand[xc]]]};zx[A1_,A2_,i_]:={(*过任意两点的直线方程/系数*)Module[{a=A1,b=A2},{w1=AppendTo[a,1];w2=AppendTo[b,1];fc=Det[{w1,w2,{x,y,1}}];a1=First[a];b1=Last[a];a2=First[b];b2=Last[b];xs={Simplify[a1-b2],Simplify[a2-a1],Simplify[a1*b2-a2*b1]};If[i==1,Print[fc],Print[xs]]}]};jd[l1_,l2_]:={(*两个直线的交点*)m=x/.First[Solve[{First[l1]*x+Part[l1,2]*y+Last[l1]==0,First[l2]*x+Part[l2,2]*y+Last[l2]==0},{x,y}]];n=y/.Last[Solve[{First[l1]*x+Part[l1,2]*y+Last[l1]==0,First[l2]*x+Part[l2,2]*y+Last[l2]==0},{x,y}]];G={Simplify[m],Simplify[n]};Print[P]};zdd[l_]:={(*找出直线过的坐标轴上的定点(如果有)*)Module[{a=First[l],b=Part[l,2],c=Last[l]},{Print[-c/a];Print[-b/a]}]};jj[la_,lb_]:={(*两直线的夹角*)Module[{A1=First[la],A2=First[lb],B1=Part[la,2],B2=Part[lb,2]},{jj=ArcTan[A1/B1]-ArcTan[A2/B2];Print[jj]}]};xl[A_,B_]:={(*给出过两点直线的斜率*)Module[{x1=First[A],x2=First[B],y1=Part[A,2],y2=Part[B,2]},{xl=Simplify[(y1-y2)/(x1-x2)]}]};
哦对封面图在这里
封面图