傅立叶变换-描述曲线（第七章傅立叶变换）

傅立叶变换是Jean-Baptiste Joseph Fourier在研究热传导微分方程中发明的数学工具，对于一个时域上的函数可以分解为频域分量的叠加。在处理有限序列过程中我们可以把序列假设为时间序列并利用快速傅立叶变换算法得到频域分量。

对于一个非病态函数$f(x)$,我们把它表达成这样的形式

f(x)=∑n=−∞∞cne2πi(nT)xf(x)=\sum_{n=-\infty}^\infty c_n\, e^{2\pi i\left(\frac{n}{T}\right) x}

其中:

cn=1T∫−T2T2f(x)e−2πi(nT)xdxc_n = \frac{1}{T} \int_{-\frac{T}{2}}^\frac{T}{2} f(x)\, e^{-2\pi i\left(\frac{n}{T}\right) x} \, dx

对于不同的n， cnc_n 就代表了不同频率的成分幅度，参照如下示意图：

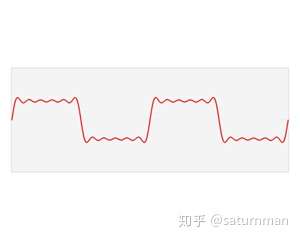
离散傅立叶变换

对于有限序列，存在快速计算离散傅立叶变换DFT的FFT算法，假设 X1,X2,...,XkX_1,X_2,...,X_k 为原有限序列，那么可以通过FFT变换获得 x1,x2,...,xnx_1,x_2,...,x_n

Xk=∑n=0N−1xne−i2πkn/Nk=0,…,N−1X_k = \sum_{n=0}^{N-1} x_n e^{-i2\pi k n/N} \qquad k = 0,\ldots,N-1

其中每个xnx_n 为复数，对于每个xnx_n，会生成一个关于频率 e−i2πn/Ne^{-i2\pi n/N}的一个序列，因为原序列是实数序列，所以每个频率序列的复数分量都会比较小，所有频率叠加后理论上复数分量消失，但是因为数值误差所以一般会保留一个很小的误差。将分量系数xnx_n按照模大小排序，选取较大的分量合成序列后就可以接近原序列。

如下图所示为将系数从大到小排列后分别选取前10，30，60，100后叠加结果与原序列的比较效果。而总的序列由800个频率分量，选取前100个分量结果已经与原序列十分接近。实际分量为复数，因为原序列为实数序列，因此随着叠加频率的增加，复数部分会逐渐趋近于零。

傅立叶变换描述运动

在古代经典宇宙结构学说，托勒密的地心说中，认为月球,太阳和其它行星都绕着地球运动，遵循本轮-均轮系统。比如月球除绕自己本轮运动，同时本轮绕着围绕地球为中心的均轮大圆运动。对于观测误差，则添加更多的本轮，采用这种模型配合观测数据可以建立非常精确有效的宇宙模型。地心说是关于宇宙结构学说的惊人成就，虽然实际这地心说不利于以太阳为参考系来描述太阳内行星运动，各种本轮过多也非常难以计算，但是其基本原理其实已经是在使用傅利叶变换在进行运动描述。

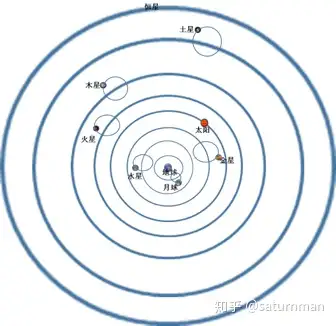
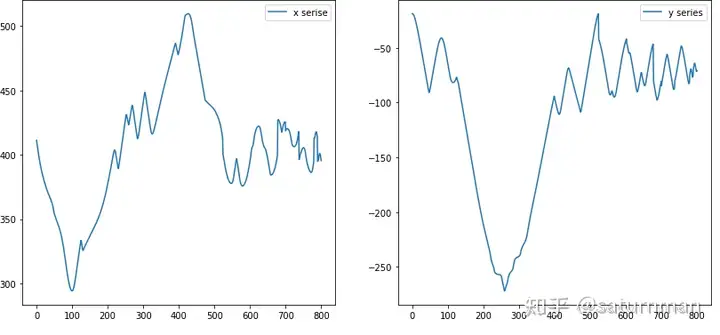
对于每一个频率分量，可以认为是围绕某个圆心以一定角速度的圆周运动，而圆的半径就是相应系数模。将比较大的频率分量做为本轮-均轮来描述运动，与实际轨迹就可以做到非常接近。 如下图对轨迹进行分解分别得到x,y分量(注:为了绘图便利将跳跃点直接连接，使整个图像成为一条联通曲线)：

傅立叶变换的应用¶

因为波动模式是现实中经常直接出现或是隐含出现的的模式，因此傅立叶变换对于异常多的模式分析有得要应用。因为傅立叶变换将时域序列的频率分量全部分解出来，重点对于大分量频率的分析一般可以抓住序列的主要特征，放弃小分量特征可以极大增加分析的便利性。图像声音信号的处理过程中放弃小分量特征可以极大压缩数据量同时降低分析与解码的计算量。

参考资料¶

[1] http://en.wikipedia.org/wiki/Fourier_transform

[2] www.youtube.com/watch?v=r6sGWTCMz2k