精确率和召回率-精确率召回率 f值

 

精确率和召回率都是二分类算法的评价指标。刚开始接触时，我们会很容易混淆精确率和召回率的概念。下面为大家区分一下这两个的概念

1.解释混淆矩阵

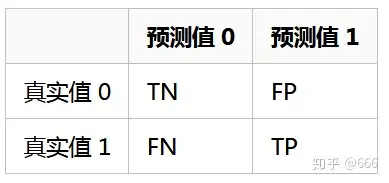
要解释清楚精确率和召回率，得先解释混淆矩阵，二分类问题的混淆矩阵由 4 个数构成。

假阴性（FN）： 算法预测为负例（N），实际上是正例（P）的个数，即算法预测错了（False）；

真阴性（TN）：算法预测为负例（N），实际上也是负例（N）的个数，即算法预测对了（True）；

真阳性（TP）：算法预测为正例（P），实际上是负例（N）的个数，即算法预测错了（False）；

假阳性（FP）：算法预测为正例（P），实际上也是正例（P）的个数，即算法预测对了（True）。

混淆矩阵定义如下：

2.精确率（precision）的定义：

精确率： precision=TPTP+FPprecision =\frac{TP}{TP+FP}

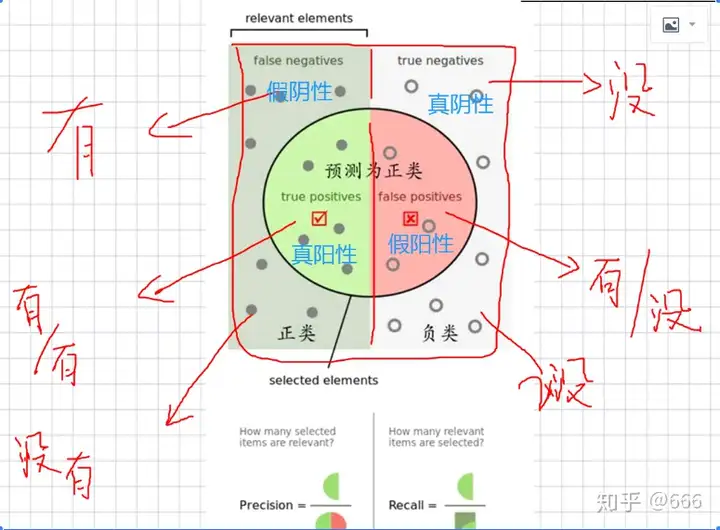
所以，精准率就是“预测为正例的那些数据里预测正确的数据个数”。

3.召回率（recall）的定义：

召回率： recall=TPTP+FNrecall =\frac{TP}{TP+FN}

所以，召回率就是“真实为正例的那些数据里预测正确的数据个数”。

借助图形加深印象：

4.调和均值

精准率和召回率是此消彼长的，即精准率高了，召回率就下降，在一些场景下要兼顾精准率和召回率，就有 F1 score。

F1值是来综合评估精确率和召回率，当精确率和召回率都高时，F1也会高

F1的公式为： 2F1=1P+1R\frac{2}{F_{1}}=\frac{1}{P}+\frac{1}{R}

有时候我们对精确率和召回率并不是一视同仁，我们用一个参数 β\beta 来度量两者之间的关系。

（）Fβ=（1+β2∗P∗R）β2∗P+RF_{\beta}=\frac{（1+\beta^{2}*P*R）}{\beta^{2}*P+R}

如果 β\beta >1，召回率有更大的影响；

如果 β\beta <1，精确率有更大的影响；

如果 β\beta =1，精确率和召回率影响力相同，和 F1F_{1} 形式一样；

5.灵敏度和特异度

灵敏度（真阳率，召回率），识别的正例占所有实际正例的比例

公式： TPR=TPTP+FNTPR = \frac{TP}{TP+FN}

特异度（假阳率），识别的假阳例占所有实际负例的比例

公式： TPR=TPTP+FNTPR = \frac{TP}{TP+FN}

看图像加深理解：

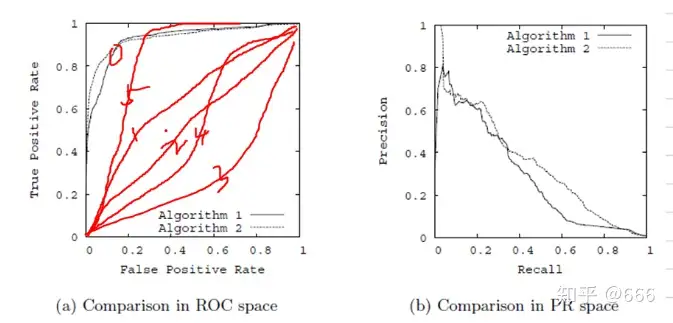
（a）假阳率比较低的情况下真阳率比较高则比较好 ROC曲线的横坐标是FPR特异度，y坐标为灵敏度

（b）算法2比较好 PR曲线的横坐标为召回率，纵坐标为精确率