用假设检验验证斯特鲁普效应-假设检验利用了什么原理
2023-06-04 23:26:22
假设检验是推论统计中用于检验统计假设的一种方法,可以用于许多场景中,今天用假设检验来验证心理学现象——斯特普鲁效应。
斯特鲁普效应是指当有一个新的刺激出现时,如果它的特征和原先的刺激相似或符合一致,便会加速人们的认知;反之,若新的刺激特征与原先的刺激不相同,则会干扰人们的认知,使人们的所需的反应时间变长。
下面将用一个试验的数据通过假设检验来验证斯特普鲁效应,试验是两组表示颜色的词语,一组,第一组字体颜色与词语表示的颜色一致,第二组字体颜色与词语表示的颜色不一致,要求同一组测试人员以最快速度说出这些词语的颜色,分别记录说出两组词语的时间。

按照以下步骤对试验数据进行假设检验:
定义问题找到证据,计算p值确定置信区间将p值与判断标准比较,得出结论# 载入库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import stats
# 载入数据
data = pd.read_csv(test.csv)
data.head()
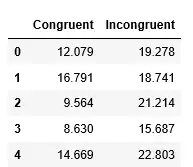
首先定义一对互斥假设,零假设和备选假设。
零假设:说出第一组词语时间与说出第二组词语时间相等,即第一组数据均值-第二组数据均值=0
备选假设:说出第一组词语时间小于说出第二组词语时间,,即第一组数据均值-第二组数据均值<0
# 数据集信息
data.info()

试验是在同一组试验个体进行的,因此属于相关配对检验,样本数据有24组,抽样分布属于t分布,备选假设包含<号,是左尾检验。
# 两组数据的分布图
plt.figure(figsize=(10,8))
sns.distplot(data.Congruent, label=Congruent)
sns.distplot(data.Incongruent, label=Incongruent)
plt.xlabel()
plt.legend()
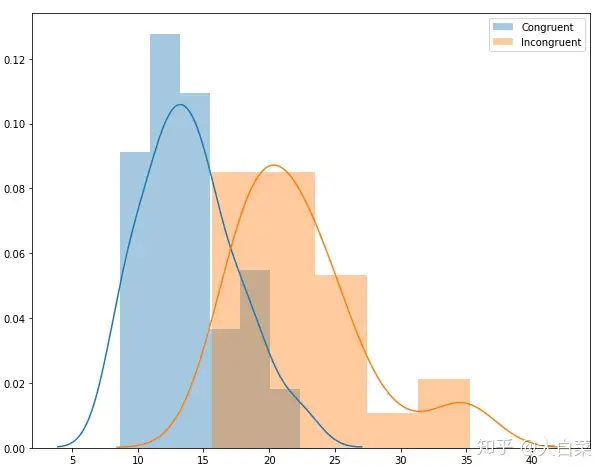
从两组数据分布可以看到,虽然实验数据量小于30,两组数据分布都接近于正态分布。
# 数据集的统计信息
data.describe()
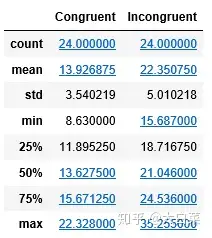
# 两组数据的柱状图
data.plot.bar(figsize=(10,8))
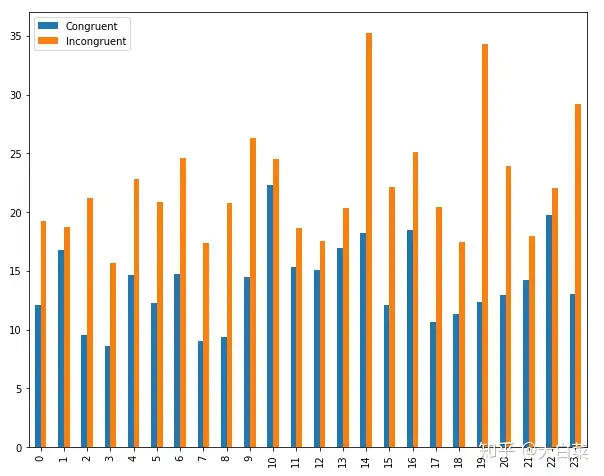
第一组数据的均值和中位数都小于第二组数据,而且每个样本对应的第一组数据都比第二组数据小。
# 两组数据差值的分布
plt.figure(figsize=(10,8))
sns.distplot(data.Congruent - data.Incongruent)
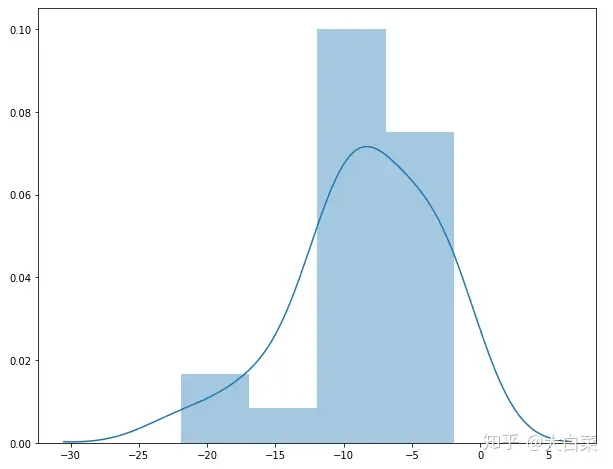
两组数据的差值分布接近正态分布。
接下来是计算p值,比较p值和判断标准,并得出结论,如果拒绝零假设,即接受备选假设,就计算其置信区间和效应量。
# 计算p值,比较p值和判断标准,并得出结论,如果拒绝零假设,即接受备选假设,就计算其置信区间和效应量
def LeftTail_Test(data1, data2, pop_mean, c=0.05):
t, p_twotail = stats.ttest_rel(data1, data2)
p_onetail = p_twotail / 2 # 计算p值
if (t < pop_mean and p_onetail < c): # p值与证据比较
print (拒绝零假设,有统计显著差异)
print (即接受备选假设,斯特普鲁效应存在)
print (\n请查找t表格中%d的置信水平、自由度为%d对应的t值,并输入方框中 % ((1-c)*100, data1.shape[0]-1))
t_ci = np.float(input())
sub = data1 - data2
sample_mean = sub.mean()
se = stats.sem(sub) # 计算标准误差
a = sample_mean - t_ci * se # 置信区间下限
b = sample_mean + t_ci * se # 置信区间上限
print (\n两组数据平均值差值在%d置信水平的置信区间为:CI=[%f, %f]% ((1-c)*100, a, b))
sample_std = sub.std()
d = (sample_mean - pop_mean) / sample_std # 计算效应量
print (\n效应量d=,d)
d = abs(d)
if d < 0.2: # 判断差异大小
print (效果差异极小)
elif (d >= 0.2 and d < 0.5):
print (效果差异小)
elif (d >= 0.5 and d < 0.8):
print (效果差异中等)
elif (d > 0.8):
print (效果差异大)
else:
print(接受零假设,没有统计显著差异,即斯特普鲁效应不存在)
LeftTail_Test(data.Congruent, data.Incongruent, 0, c=0.05)
下图为函数输出结果:

通过以上假设检验可知存在斯特普鲁现象。
以上就是关于《用假设检验验证斯特鲁普效应-假设检验利用了什么原理》的全部内容,本文网址:https://www.7ca.cn/baike/43439.shtml,如对您有帮助可以分享给好友,谢谢。
声明
